- ИНТЕРПОЛЯЦИОННЫЙ ПРОЦЕСС
- процесс получения последовательности интерполирующих функций {fn(z)} при неограниченном возрастании числа n условий интерполирования. Если интерполирующие функции fn(z)представлены в виде частных сумм некоторого функционального ряда, то последний иногда наз.
интерполяционным рядом. Целью построения И. п. чаще всего является, по крайней мере в простейших первоначальных задачах интерполирования, приближение в каком-то смысле посредством интерполирующих функций fn(z)исходной функции f (z), о к-рой или имеется неполная информация или форма к-рой слишком сложна для непосредственного использования.
Довольно общая ситуация, связанная с построением И. п., описывается следующим образом. Пусть (a/ft),
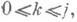j=0, 1, ...- бесконечная треугольная таблица произвольно заданных комплексных чисел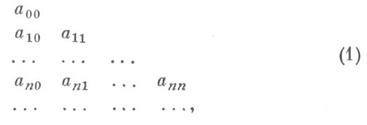
наз. узлами интерполяции. Пусть, наряду с таблицей (1), имеется таблица аналогичного вида (wjk),
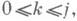j=0, 1, ..., также составленная из произвольно заданных комплексных чисел wjk.Если в п-и строке а nk, k = 0,1, . .., п, таблицы узлов (1) нет совпадающих чисел, или, как еще говорят, вся эта строка состоит из простых узлов, то, пользуясь, напр., Лагранжа интерполяционной формулой, строится (единственный) алгебраический интерполяционный многочлен р п(z) степени ве выше п, удовлетворяющий простым условиям интерполяции
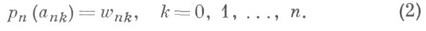
Если же точка а п0 является кратным узлом кратности v0>l в п-в. строке, т. е. встречается в этой строке v0 раз: an0=ank1=...= ankv0_1, то соответствующие условия кратного интерполирования в узле а n0 имеют вид
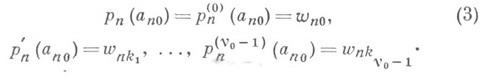
В общем случае при наличии кратных узлов (единственный) алгебраический интерполяционный многочлен pn(z)степени не выше пстроится по этим условиям, напр., по Эрмита интерполяционной формуле. В качестве примера системы узлов (1) можно привести систему j+1, j=0, 1, . . ., равноотстоящих узлов а jk=e2pik/(j+1) на единичной окружности, применяемую в случае так наз. интерполяции в корнях из единицы (см. [5]).
В результате осуществляемого таким путем И. п. получается последовательность интерполяционных многочленов {pn(z)}, определяемая таблицами (ajk) и (wjk). Основными вопросами, здесь возникающими, являются: определить в зависимости от (ajk) и (wjk )множество EМ C точек сходимости последовательности {pn(z)}, в к-рых существует предел
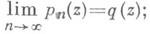определить характер предельной функции g(z); определить множество FМ E, на к-ром сходимость pn(z)
q(z). равномерная; и т. д.В теории функций комплексного переменного наиболее изучен случай, когда таблица (wjk) строится по . значениям регулярной аналитич. функции f(z) и ее производных в узлах интерполяции так, что (применительно к узлу а п0 кратности
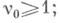ср. (3))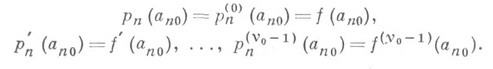
В этом случае интерполяционный многочлен р п(r)можно записать по формуле Эрмита в виде интеграла по контуру Г, охватывающему узлы ank, k = 0, 1, ..., п, на к-ром и внутри к-рого f(z)регулярна:
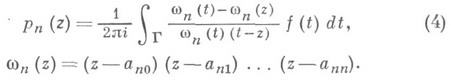
Из формулы (4) легко получается и интегральное представление остаточного члена интерполяции Rn(z)=f(z)-pn(z). Вообще говоря, последовательность {pn(z)}, построенная по f(z), может расходиться. Если же она сходится, то предельная функция q(z)может не совпадать с f(z). Основным вопросом является изучение сходимости {pn(z)}к f(z) и нахождение таких систем узлов (ajk), для к-рых сходимость в каком-то смысле оптимальная. Пусть, напр., функция f(z) регулярна на континууме
содержащем не менее двух точек, дополнение к-рого до расширенной плоскости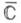 
есть односвязная область, содержащая бесконечно удаленную точку. Пусть узлы (a/ft) принадлежат К. Тогда для того, чтобы И. п. {pn(z)}равномерно сходился на Кк f(z), необходимо и достаточно, чтобы выполнялось условие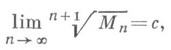
где Mn=sup {|wn(z)|;
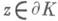}, с - емкость множества К (см. [4]).Классический вариант И. п. получается, когда узлы ajk=ak.
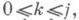j=0, 1, .. ., составляют последовательность {ak}, из к-рой на n-м шаге для получения многочлена р n(z) используются первые n+1 узлов а 0, а 1, ..., а п. В этом случае для регулярной функции f(z)многочлены р n(z) суть частные суммы интерполяционного ряда Ньютона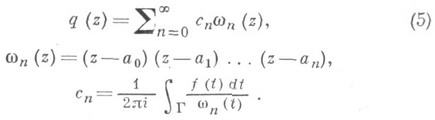
При вычислениях интерполяционный ряд вида (5) имеет то преимущество перед последовательностью {р n(z)}, что для перехода от уже известного многочлена pn(z)к pn+1(z). необходимо вычислить только один коэффициент ряда с n+1. В зависимости от расположения узлов ak и значений коэффициентов с k, областью сходимости ряда Ньютона может быть любая односвязная область плоскости С с аналитич. раницей. В частности, напр., если последовательность узлов {ak} имеет предельную точку только в бесконечности,
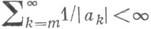и ряд (5) сходится хотя бы в одной точке 
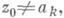k=0, 1, ..., то он сходится равномерно в любом круге 
и, следовательно, его сумма q(z)есть целая функция. Интерполяционный ряд Стирлинга есть частный случай ряда Ньютона для последовательности узлов a0 = 0, а 1=-1, а 2 = 1, ..., a2k-1=-k,a2k= k, ... Исследованы и другие разновидности интерполяционных рядов (см. [3], [5]).Объектами изучения являются также И. п. с неалгебраическими интерполяционными полиномами pn(z) =
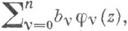составленными по другим системам функций {jv(z)}, отличным от системы степеней {zv}, напр., по системе {eavz} (см. [4], [6]).Изучение И. п. в действительной области имеет свою специфику как в постановке задач, так и в результатах (см. [2], [4]). Эта специфика обусловлена прежде всего естественным в действительной области отказом от требования регулярности интерполируемой функции f(x). Известно, напр., что никакая система узлов на отрезке [а, b]не гарантирует сходимости И. п. для произвольной непрерывной функции f(x),
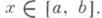С другой стороны, если непрерывная функция f(х)наперед задана, то всегда можно выбрать систему узлов так, чтобы И. п. сходился к f(x).Кроме И. п. с интерполяционными полиномами pn(z)внимание исследователей привлекают И. п. с рациональными функциями rn(z), напр, вида rn(z)= qn(z)/wn_1(z), где wn_1(z)=(z-b0) ...(z-bn-1) и qn(z)- многочлен степени не выше п. Условия интерполяции (1) - (3) остаются в силе, но теперь должно быть добавлено условие на полюсы bk, k=0,1,..., к-рые в простейшем случае задаются в виде треугольной таблицы (bjk),
j=0, 1, ..., аналогичной (1).См. также Абеля- Гончарова проблема, Бернштейна интерполяционный процесс.
Лит.:[1] Маркушевич А. И., Теория аналитических функций, т. 1, 2 изд., М., 1967; [2] Гончаров В. Л., Теория интерполирования и приближения функций, 2 изд., М., 1954; [3] Гельфонд А. О., Исчисление конечных разностей, 2 изд., М., 1959; [4] Смирнов В. И., Лебедев Н. А., Конструктивная теория функций комплексного переменного, М., 1964; [5] У олш Дж. Л., Интерполяция и аппроксимация рациональными функциями в комплексной области, пер. с англ., М., 1961; [6] Леонтьев А. Ф., Ряды экспонент, М., 1976.
Е. Д. Соломенцев.
Математическая энциклопедия. — М.: Советская энциклопедия. И. М. Виноградов. 1977—1985.
