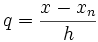Интерполяционная формула Ньютона
- Интерполяционная формула Ньютона
-
Интерполяционные формулы Ньютона — формулы вычислительной математики, применяющиеся для полиномиального интерполирования.
Если узлы интерполяции равноотстоящие и упорядочены по величине, так что xi + 1 − xi = h = const, то есть xi = x0 + ih, то интерполяционный многочлен можно записать в форме Ньютона.
Интерполяционные полиномы в форме Ньютона удобно использовать, если точка интерполирования находится вблизи начала (прямая формула Ньютона) или конца таблицы (обратная формула Ньютона).
Короткая форма интерполяционной формулы Ньютона
В случае равноудаленных центров интерполяции, находящихся на единичном расстоянии друг от друга, справедлива формула:
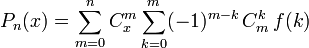
где 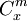 — обобщенные на область действительных чисел биномиальные коэффициенты.
— обобщенные на область действительных чисел биномиальные коэффициенты.
Прямая интерполяционная формула Ньютона
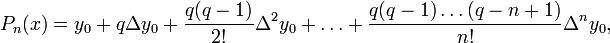 где
где 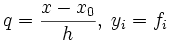 , а выражения вида Δkyi — конечные разности.
, а выражения вида Δkyi — конечные разности.
Обратная интерполяционная формула Ньютона
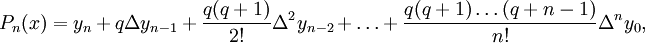 где
где 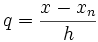
См. также
Wikimedia Foundation.
2010.
Полезное
Смотреть что такое "Интерполяционная формула Ньютона" в других словарях:
ИНТЕРПОЛЯЦИОННАЯ ФОРМУЛА — формула для приближенного вычисления значений функции f(x), основанного на замене приближаемой функции f(x)более простой в каком то смысле функцией наперед заданного класса, причем параметры ai, i=0, 1, ..., п, выбираются таким образом, чтобы… … Математическая энциклопедия
Интерполяционная формула — Интерполяционные формулы, формулы, дающие приближённое выражение функции при помощи интерполяции, то есть через интерполяционный многочлен степени , значения которого в заданных точках совпадают со значениями … Википедия
НЬЮТОНА ИНТЕРПОЛЯЦИОННАЯ ФОРМУЛА — форма записи Лагранжа интерполяционной формулы, использующая разделенные разности: где разделенные разности k гопорядка; рассматривалась И. Ньютоном (I. Newton, 1687). Формула (1) наз. Н. и. ф. для неравных промежутков. В случае, когда значения… … Математическая энциклопедия
Интерполяционные формулы Ньютона — Интерполяционные формулы Ньютона формулы вычислительной математики, применяющиеся для полиномиального интерполирования. Если узлы интерполяции равноотстоящие и упорядочены по величине, так что , то есть , то интерполяционный многочлен можно … Википедия
Интерполяционный многочлен Ньютона — Интерполяционные формулы Ньютона формулы вычислительной математики, применяющиеся для полиномиального интерполирования. Если узлы интерполяции равноотстоящие и упорядочены по величине, так что xi + 1 − xi = h = const, то есть xi = x0 + ih, то… … Википедия
Интреполирование по формулам Ньютона — Интерполяционные формулы Ньютона формулы вычислительной математики, применяющиеся для полиномиального интерполирования. Если узлы интерполяции равноотстоящие и упорядочены по величине, так что xi + 1 − xi = h = const, то есть xi = x0 + ih, то… … Википедия
НЬЮТОНА- КОТЕСА КВАДРАТУРНАЯ ФОРМУЛА — интерполяционная квадратурная формула для вычисления интеграла по конечному промежутку [а, b], узлы к рой выбираются следующим образом: где п натуральное число и , число узлов N= n+l. Коэффициенты определяются тем, что квадратурная формула… … Математическая энциклопедия
КВАДРАТУРНАЯ ФОРМУЛА — приближенная формула для вычисления определенного интеграла: в левой части стоит интеграл, подлежащий вычислению. Подинтегральная функция записана в виде произведения двух функций. Первая из них р(х)считается фиксированной для данной К. ф. и наз … Математическая энциклопедия
Интерполяционные формулы — Интерполяционные формулы в математике формулы, дающие приближённое выражение функции при помощи интерполяции, то есть через интерполяционный многочлен степени , значения которого в заданных точках совпадают со значениями функции в этих… … Википедия
Интерполяционные формулы — формулы, дающие приближённое выражение функции у = f (x) при помощи интерполяции (См. Интерполяция), т. е. через интерполяционный многочлен Рn(х) степени n, значения которого в заданных точках x0, x1, ..., хn совпадают со значениями y0,… … Большая советская энциклопедия
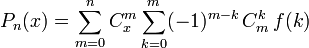
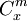 — обобщенные на область действительных чисел биномиальные коэффициенты.
— обобщенные на область действительных чисел биномиальные коэффициенты.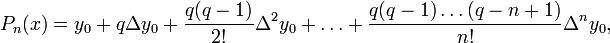 где
где 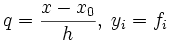 , а выражения вида Δkyi — конечные разности.
, а выражения вида Δkyi — конечные разности.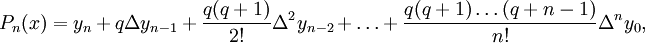 где
где