Гурвица критерий

Критерий устойчивости Гурвица — один из способов анализа линейной стационарной динамической системы на устойчивость, разработанный немецким математиком Адольфом Гурвицем. Наряду с критерием Рауса является представителем семейства алгебраических критериев устойчивости, в отличие от частотных критериев, таких как критерий устойчивости Найквиста. К достоинствам метода относятся простая реализация на ЭВМ, а к недостаткам — малая наглядность.

Формулировка

Метод работает с коэффициентами характеристического уравнения системы. Пусть 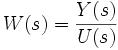$W(s) = \frac{Y(s)} {U(s)}$ — передаточная функция системы, а 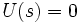$\ U(s) = 0$ — характеристическое уравнение системы. Представим характеристический полином 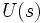$\ U(s)$ в виде

$\ U(s) = a_0 s^n + a_1 s^{n-1} + ... + a_n$

Из коэффициентов характеристического уравнения строится определитель Гурвица 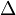$\Delta\$ по алгоритму:

1) по главной диагонали слева направо выставляются все коэффициенты характеристического уравнения от 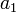$\ a_1$ до $\ a_n$

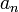
2) от каждого элемента диагонали вверх и вниз достраиваются столбцы определителя так, чтобы индексы убывали сверху вниз;

3) на место коэффициентов с индексами меньше нуля или больше 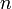$\ n$ ставятся нули.

Тогда согласно критерию Гурвица:

Для того, чтобы динамическая система была устойчива, необходимо и достаточно, чтобы все 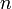$\ n$ диагональных миноров определителя Гурвица были положительны. Эти миноры называются определителями Гурвица.

См. также

• Критерий устойчивости Рауса
• Критерий устойчивости Найквиста — Михайлова
• Теорема Рауса—Гурвица

Система находится на границе апериодической устойчивости, если a с индексом n будет равна 0. Система находится на границе колебательной устойчивости, если определитель Гурвица с индексом (n-1) будет равным 0.

Литература

Четаев Н.Г. Устойчивость движения.— Москва: Наука, 1965.—234 с.