- Критерий устойчивости Найквиста — Михайлова
-
Критерий устойчивости Найквиста — Михайлова
Критерий устойчивости Найквиста — Михайлова — один из способов судить об устойчивости замкнутой системы управления по её разомкнутой АФЧХ. Является одним из частотных критериев устойчивости. С помощью этого критерия оценить устойчивость весьма просто, без необходимости вычисления полюсов передаточной функции замкнутой системы.
Содержание
Условие устойчивости
Передаточная функция динамической системы
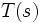 может быть представлена в виде дроби
может быть представлена в виде дроби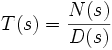 .
.
Устойчивость
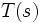 достигается тогда, когда все её полюса находятся в левой полуплоскости на плоскости корней. В правой полуплоскости их быть не должно. Если
достигается тогда, когда все её полюса находятся в левой полуплоскости на плоскости корней. В правой полуплоскости их быть не должно. Если 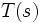 получена замыканием отрицательной обратной связью разомкнутой системы с передаточной функцией
получена замыканием отрицательной обратной связью разомкнутой системы с передаточной функцией 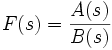 , тогда полюса передаточной функции замкнутой системы являются нулями функции
, тогда полюса передаточной функции замкнутой системы являются нулями функции 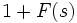 Выражение
Выражение 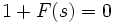 называется характеристическим уравнением системы.
называется характеристическим уравнением системы.Принцип аргумента Коши
Из теории функций комплексного переменного известно, что контур
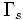 охватывающий на
охватывающий на  -плоскости некоторое число неаналитических точек может быть отображён на другую комплексную плоскость (плоскость
-плоскости некоторое число неаналитических точек может быть отображён на другую комплексную плоскость (плоскость  ) при помощи функции
) при помощи функции  таким образом, что получившийся контур
таким образом, что получившийся контур 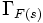 будет охватывать центр
будет охватывать центр 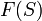 -плоскости
-плоскости 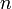 раз, причём
раз, причём 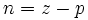 , где
, где 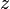 — число нулей, а
— число нулей, а 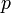 — число полюсов функции
— число полюсов функции  . Положительным считается направление, совпадающее с направлением контура
. Положительным считается направление, совпадающее с направлением контура 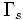 , а отрицательным — противоположное ему.
, а отрицательным — противоположное ему.Формулировка критерия
Сначала построим контур, охватывающий правую полуплоскость комплексной плоскости. Контур состоит из следующих участков:
- участок, идущий вверх по оси
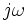 , от
, от 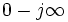 до
до 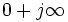 .
. - полуокружность радиусом
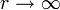 , начинающаяся в точке
, начинающаяся в точке 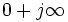 и достигающая конца в точке
и достигающая конца в точке 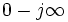 по часовой стрелке.
по часовой стрелке.
Далее отображаем этот контур посредством передаточной функции разомкнутой системы
 , в результате чего получаем плоскость АФЧХ системы. Согласно принципу аргумента число оборотов по часовой стрелке вокруг начала координат должно быть равно количеству нулей функции
, в результате чего получаем плоскость АФЧХ системы. Согласно принципу аргумента число оборотов по часовой стрелке вокруг начала координат должно быть равно количеству нулей функции  минус количество полюсов
минус количество полюсов  в правой полуплоскости. Если рассматривать вместо начала координат точку
в правой полуплоскости. Если рассматривать вместо начала координат точку 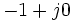 , получим разницу между числом нулей и полюсов в правой полуплоскости для функции
, получим разницу между числом нулей и полюсов в правой полуплоскости для функции 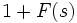 . Заметив, что функция
. Заметив, что функция 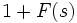 имеет такие же полюса, что и функция
имеет такие же полюса, что и функция  , а полюса разомкнутой системы являются нулями замкнутой системы, сформулируем критерий Найквиста — Михайлова:
, а полюса разомкнутой системы являются нулями замкнутой системы, сформулируем критерий Найквиста — Михайлова:Пусть
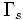 — замкнутый контур в комплексной плоскости,
— замкнутый контур в комплексной плоскости, 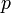 — число полюсов
— число полюсов  , охваченных контуром
, охваченных контуром 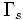 , а
, а 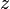 — число нулей
— число нулей  , охваченных
, охваченных 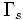 — то есть число полюсов
— то есть число полюсов 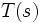 охваченных
охваченных 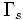 . Получившийся контур в
. Получившийся контур в  -плоскости,
-плоскости, 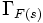 должен для обеспечения устойчивости замкнутой системы охватывать (по часовой стрелке) точку
должен для обеспечения устойчивости замкнутой системы охватывать (по часовой стрелке) точку 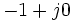
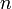 раз, где
раз, где 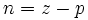 .
.Следствия критерия Найквиста-Михайлова:
- Если разомкнутая система с передаточной функцией
 устойчива, замкнутая система является устойчивой, если АФЧХ разомкнутой системы не охватывает точку −1.
устойчива, замкнутая система является устойчивой, если АФЧХ разомкнутой системы не охватывает точку −1. - Если разомкнутая система неустойчива, то количество оборотов
 вокруг точки −1 должно быть равно числу полюсов
вокруг точки −1 должно быть равно числу полюсов  в правой полуплоскости.
в правой полуплоскости. - Количество дополнительных охватов (больше, чем
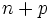 ) вокруг точки −1 в точности равно количеству неустойчивых полюсов замкнутой системы.
) вокруг точки −1 в точности равно количеству неустойчивых полюсов замкнутой системы.
См. также
- Критерий устойчивости Рауса
- Критерий устойчивости Гурвица
- Критерий устойчивости в пространстве состояний
- ЛАФЧХ
- Электронный усилитель
- Генератор (электроника)
Wikimedia Foundation. 2010.
Критерий устойчивости Найквиста-Михайлова — Критерий устойчивости Найквиста Михайлова один из способов судить об устойчивости замкнутой системы управления по её разомкнутой АФЧХ. Является одним из частотных критериев устойчивости. С помощью этого критерия оценить устойчивость весьма… … Википедия
Критерий устойчивости Найквиста — Критерий устойчивости Найквиста Михайлова один из способов судить об устойчивости замкнутой системы управления по амплитудно фазовой частотной характеристике её разомкнутого состояния. Является одним из частотных критериев… … Википедия
Критерий устойчивости Рауса — Критерий устойчивости Рауса один из методов анализа линейной стационарной динамической системы на устойчивость. Наряду с критерием Гурвица (который часто называют критерием Рауса Гурвица) является представителем семейства… … Википедия
Критерий устойчивости Гурвица — Критерий устойчивости Рауса Гурвица один из способов анализа линейной стационарной динамической системы на устойчивость, разработанный немецким математиком Адольфом Гурвицом. Наряду с критерием Рауса является представителем семейства… … Википедия
Критерий устойчивости Рауса-Гурвица — Критерий устойчивости Гурвица один из способов анализа линейной стационарной динамической системы на устойчивость, разработанный немецким математиком Адольфом Гурвицем. Наряду с критерием Рауса является представителем семейства алгебраических… … Википедия
Михайлова критерий — Критерий устойчивости Найквиста Михайлова один из способов судить об устойчивости замкнутой системы управления по её разомкнутой АФЧХ. Является одним из частотных критериев устойчивости. С помощью этого критерия оценить устойчивость весьма… … Википедия
Критерий Рауса — Критерий устойчивости Рауса один из методов анализа линейной стационарной динамической системы на устойчивость. Наряду с критерием Гурвица (который часто называют критерием Рауса Гурвица) является представителем семейства алгебраических критериев … Википедия
Критерий Гурвица — Критерий устойчивости Гурвица один из способов анализа линейной стационарной динамической системы на устойчивость, разработанный немецким математиком Адольфом Гурвицем. Наряду с критерием Рауса является представителем семейства алгебраических… … Википедия
Гурвица критерий — Критерий устойчивости Гурвица один из способов анализа линейной стационарной динамической системы на устойчивость, разработанный немецким математиком Адольфом Гурвицем. Наряду с критерием Рауса является представителем семейства алгебраических… … Википедия
График Найквиста — Амплитудно фазовая частотная характеристика (АФЧХ) удобное представление частотного отклика линейной стационарной динамической системы в виде графика в полярных координатах. На таком графике частота выступает в качестве параметра кривой, фаза и… … Википедия
