Борелевская алгебра

Борелевская сигма-алгебра — это минимальная сигма-алгебра, содержащая все открытые подмножества топологического пространства (впрочем, она содержит и все замкнутые).

Если не оговорено противное, в качестве топологического пространства выступает множество вещественных чисел.

Борелевская сигма-алгебра обычно выступает в роли сигма-алгебры случайных событий вероятностного пространства. В борелевской сигма-алгебре на прямой или на отрезке содержатся многие «простые» множества: все интервалы, полуинтервалы, отрезки и их счётные объединения.

Алгебра была названа по имени Бореля.

Связанные понятия

• Борелева (борелевская) функция — отображение одного топологического пространства в другое (обычно оба суть пространства вещественных чисел), для которого прообраз любого борелевского множества есть борелевское множество.

Свойства

• Построение неборелевских множеств на прямой возможно лишь с использованием аксиомы выбора
• Всякое борелевское множество на отрезке является измеримым относительно меры Лебега, но обратное не верно.

Пример измеримого по Лебегу, но не борелевского множества

Рассмотрим функцию 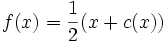$f(x) = \frac{1}{2}(x+c(x))$ на отрезке $[0,\;1]$, где c(x) — функция Кантора. Мера образа канторова множества равна $\frac{1}{2}$, а значит, мера образа его дополнения также равна $\frac{1}{2}$. Функция f(x) монотонна, значит, она измерима и существует обратная к ней функция. Поскольку мера образа канторова множества ненулевая, в нём можно найти неизмеримое множество A. Тогда образ A при отображении f ^{− 1} будет измеримым (так как он лежит в канторовом множестве, мера которого нулевая), но не будет борелевским (поскольку иначе A было бы измеримо как прообраз борелевского множества при измеримом отображении).