КАСАТЕЛЬНОЕ РАССЛОЕНИЕ

КАСАТЕЛЬНОЕ РАССЛОЕНИЕ

дифференцируемого многообразия М- вектор ное расслоение х: 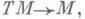пространство к-рого ТМ является касательным пространством к М(объединением касательных пространств ТМ|x в точке 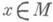), состоящим из касательных векторов к М, а проекция t отображает ТМ|x в х. Сечение К. р. х(М)- векторное поле на многообразии М. Атлас многообразия ТМ определяется атласом многообразия Ми условием локальной тривиальности расслоения т (М). Функции перехода К. р. являются матрицами Якоби функций перехода атласа многообразия.

К К. р. присоединено главное расслоение реперов многообразия М. Расслоение х* (М), двойственное К. р. х(М), наз. кокасательным расслоением, а его пространство Т*М- кокасательным пространством. Сечениями его являются линейные дифференциальные формы ( Пфаффа формы).

Дифференцируемое отображение h: M->N индуцирует морфизм К. р. соответствующее отображение касательных пространств hT: наз. касательным к hотображением. В частности, если i:- иммерсия, то х(М)является подрасслоением индуцированного расcлоения i*t(N). Факторрасслоение v(i)=i*x(M)/t(M)наз. нормальным расслоение м иммерсии. Двойственно, если j : -субмерсия, то факторрасслоение х(М)/j*t(М)наз. субрасслоением j. Если в качестве Ми N взяты соответственно ТМ и М,a h=t: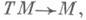 то t*t(М)наз. вторым касательным расслоением.

Если К. р. х(М)- тривиально, то Мназ. параллелизуемым многообразием.

Лит.:[1] Годбийон К., Дифференциальная геометрия и аналитическая механика, пер. с франц., М., 1973.

М. И. Войцеховский.


Математическая энциклопедия. — М.: Советская энциклопедия. . 1977—1985.

Игры ⚽ Нужно решить контрольную?

Полезное


Смотреть что такое "КАСАТЕЛЬНОЕ РАССЛОЕНИЕ" в других словарях:

  • Касательное расслоение — Неформально, касательное расслоение многообразия (в данном случае окружности) получается при рассмотрении всех касательных пространств (сверху) и объединении их гладко без пересечений (снизу) Касательное расслоение …   Википедия

  • Касательное пространство — и касательный вектор …   Википедия

  • РАССЛОЕНИЕ — (расслоённое пространство) одна из фундам. структур, изучаемых в топологии. В совр. физике, гл. обр. в теории элементарных частиц, концепция Р. и ассоциированных с ним матем. структур (связность и т. п.) является наиб. адекватным языком для… …   Физическая энциклопедия

  • Векторное расслоение — Векторным расслоением называется определённая геометрическая конструкция, соответствующая семейству векторных пространств, параметризованных другим пространством (например, может быть топологическим пространством, многообразием или алгебраической …   Википедия

  • ПОЛОЖИТЕЛЬНОЕ РАССЛОЕНИЕ — обобщение понятия дивизора положительной степени на римановой поверхности. Голоморфное векторное расслоение Енад комплексным пространством Xназ. положительным (обозначается E>0), если в Есуществует такая эрмитова метрика h, что функция на… …   Математическая энциклопедия

  • ВЕКТОРНОЕ АНАЛИТИЧЕСКОЕ РАССЛОЕНИЕ — локально тривиальное аналитич. расслоение над аналитич. ространством, слои к рого обладают структурой n мерного векторного пространства над основным полем k(если иоле комплексных чисел, то аналитич. расслоение наз. также голоморфны м). Число пназ …   Математическая энциклопедия

  • ВЕКТОРНОЕ АЛГЕБРАИЧЕСКОЕ РАССЛОЕНИЕ — морфизм многообразий , локально (в Зариского топологии).устроенный как проекция прямого произведения на , причем склейка сохраняет послойно структуру векторного пространства. При этом Еназ. пространством расслоения, базой, а п рангом (или… …   Математическая энциклопедия

  • Гладкое расслоение — Гладкое расслоение  локально тривиальное расслоение с гладкими функциями перехода. Содержание 1 Определение 2 Примеры 3 Свойства …   Википедия

  • Ко-касательное пространство — Кокасательное пространство (иногда неверно ко касательное пространство)  пространство, двойственное (сопряженное) касательному. Кокасательное пространство к гладкому многообразию M в точке p обычно обозначается . Сечениями кокасательного… …   Википедия

  • Локально тривиальное расслоение — расслоение, которое локально выглядит как прямое произведение. Содержание 1 Определение 2 Связанные определения 3 Примеры …   Википедия


Поделиться ссылкой на выделенное

Прямая ссылка:
… Нажмите правой клавишей мыши и выберите «Копировать ссылку»