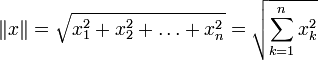Эвклидово пространство

В математике термин евкли́дово простра́нство может обозначать один из сходных и тесно связанных объектов:

В обоих случаях, n-мерное евклидово пространство обычно обозначается 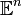$\mathbb E^n$, хотя часто используется не вполне приемлемое обозначение $\mathbb R^n$.

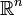1. Конечномерное вещественное векторное пространство 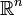$\mathbb R^n$ с введённым на нём (положительно определенным) скалярным произведением, порождающим норму:

$\|x\|=\sqrt{\langle x, x \rangle}$,

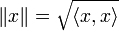в простейшем случае (евклидова норма):

$\|x\|=\sqrt{x_1^2+x_2^2+\dots +x_n^2} = \sqrt{\sum_{k=1}^n x_k^2}$

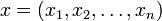где $x=(x_1,x_2,\dots, x_n)$ (в евклидовом пространстве всегда можно выбрать базис, в котором верен именно этот простейший вариант).

Иначе говоря евклидово пространство — конечномерное гильбертово пространство.

2. Метрическое пространство, которое является конечномерным векторным пространством 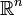$\mathbb R^n$ над полем вещественных чисел с евклидовой метрикой, введённой по формуле:

$d(x,y)=\sqrt{(x_1-y_1)^2+(x_2-y_2)^2+\dots+(x_n-y_n)^2} = \sqrt{\sum_{k=1}^n (x_k-y_k)^2}$,

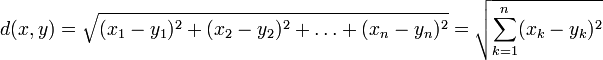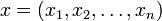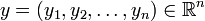где $x=(x_1,x_2,\dots, x_n)$ и $y=(y_1,y_2,\dots, y_n)\in \mathbb R^n$, то есть с функцией расстояния, порождаемой описанной выше нормой.

Связанные определения

• Под евклидовой метрикой может пониматься метрика, описанная выше, а также соответствующая риманова метрика.

• Под локальной евклидовостью обычно имеют в виду то, что каждое касательное пространство риманова многообразия есть евклидово пространство со всеми вытекающими свойствами, например, возможностью (по гладкости метрики) ввести в малой окрестности точки координаты, в которых расстояние выражается (с точностью до какого-то порядка) в соответствии с описанным выше.

• Метрическое пространство называют локально евклидовым также если возможно ввести на нём координаты, в которых метрика будет евклидовой (в смысле второго определения) всюду (или хотя бы на конечной области) - каковым, например, является риманово многообразие нулевой кривизны.

Примеры

Наглядными примерами евклидовых пространств могут служить пространства:

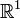• $\R^1$ размерности 1 (вещественная прямая)
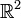• $\R^2$ размерности 2 (евклидова плоскость)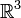
• $\R^3$
• Евклидово пространство можно считать современной интерпретацией и обобщением (т.к. оно допускает размерности больше трех) классической (Евклидовой) геометрии.

Можно привести и несколько более абстрактные примеры:

• пространство вещественных полиномов степени, не превосходящей n, со скалярным произведением, определенным как интеграл произведения по конечному отрезку (или по всей прямой, но с быстро спадающей весовой функцией)
• вообще пространство всех линейных комбинаций конечного набора вещественных функций
• пространство состояний конечномерной квантовой системы (или конечномерное подпространство полного пространства состояний) в вещественном представлении.

Не считается обычно евклидовым физическое 4-мерное пространство-время, т.к. основная метрика на нём, в соответствии с обычным в современной физике взглядом, псевдоевклидова. Хотя при желании евклидовская метрика может быть формально введена на нём тем или иным образом (если не пренебрегать гравитацией — то локально), что бывает иногда полезно, однако она не лоренц-инвариантна, что здесь очень сильно снижает её ценность с точки зрения современной физики.

См. также

• Гильбертово пространство
• Псевдоевклидово пространство
• Евклидова геометрия
• Евклидово поле

Ссылки