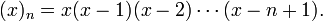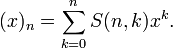Число Стирлинга первого рода
- Число Стирлинга первого рода
-
Числа Стирлинга первого рода — количество перестановок из n предметов, имеющие ровно k циклов.
Определение
Введём следующее семейство многочленов от x, параметризованное неотрицательным целым числом n:
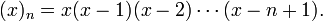
Числами Стирлинга первого рода S(n, k) по определению называются коэффициенты такого многочлена:
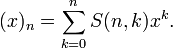
Как видно из определения, числа имеют чередующийся знак. Их абсолютные значения задают количество перестановок множества, состоящего из n элементов, в разложении которых на непересекающиеся циклы имеется ровно k циклов.
Рекуррентное соотношение
Числа Стирлинга первого рода задаются рекуррентным соотношением:
S(n,n) = 1, для n ≥ 0,
S(n,0) = 0, для n > 0,
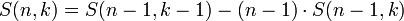 для 0 < k < n.
для 0 < k < n.
Пример
Первые ряды:
|
0 |
1 |
2 |
3 |
4 |
5 |
6 |
| 0 |
1 |
|
|
|
|
|
|
| 1 |
0 |
1 |
|
|
|
|
|
| 2 |
0 |
1 |
1 |
|
|
|
|
| 3 |
0 |
1 |
3 |
1 |
|
|
|
| 4 |
0 |
1 |
7 |
6 |
1 |
|
|
| 5 |
0 |
1 |
15 |
25 |
10 |
1 |
|
| 6 |
0 |
1 |
31 |
90 |
65 |
15 |
1 |
Свойства
См. также
Ссылки
Wikimedia Foundation.
2010.
Полезное
Смотреть что такое "Число Стирлинга первого рода" в других словарях:
Число Стирлинга второго рода — В комбинаторике числом Стирлинга второго рода S(n, k) называется число неупорядоченных разбиений n элементного множества на k непустых подмножеств. Числа Стирлинга второго рода задаются рекуррентным соотношением: S(n,n) = 1, для n ≥ 0, S(n,0) = 0 … Википедия
Числа Стирлинга первого рода — (без знака) количество перестановок порядка n с k циклами. Содержание 1 Определение 2 Рекуррентное соотношение 3 … Википедия
Числа Стирлинга второго рода — В комбинаторике числом Стирлинга второго рода из n по k, обозначаемым или , называется количество неупорядоченных разбиений n элементного множества на k непустых подмножеств. Содержание 1 Рекуррентная формула … Википедия
Числа стирлинга второго рода — В комбинаторике числом Стирлинга второго рода S(n, k) называется число неупорядоченных разбиений n элементного множества на k непустых подмножеств. Числа Стирлинга второго рода задаются рекуррентным соотношением: S(n,n) = 1, для n ≥ 0, S(n,0) = 0 … Википедия
Числа Эйлера I рода — В комбинаторике числом Эйлера I рода из n по k, обозначаемым или , называется количество перестановок порядка n с k подъёмами, то есть таких перестановок , что существует ровно k индексов j, для которых . Числа Эйлера I рода обладают также… … Википедия
Полиномы Белла — В математике, в частности в комбинаторике, полиномы Белла это полиномы вида где сумма берётся по всем последовательностям j1, j2, j3, ..., jn−k+1 неотрицательных целых чисел таким, что и … Википедия
Символ Похгаммера — Символ Похгаммера обозначение, принятое для обозначения функции, задаваемой произведением: , где целое число. Название дано по имени немецкого математика Лео Похгаммера. Символы Похгаммера удовлетворяют соотношению: . В частном случае, при… … Википедия
Парадокс дней рождения — Парадокс дней рождения это кажущееся парадоксальным утверждение, что вероятность совпадения дней рождения (числа и месяца) хотя бы у двух членов группы из 23 и более человек, превышает 50 %. С практической точки зрения это означает,… … Википедия
Ольмеки — Эта статья или раздел нуждается в переработке. Пожалуйста, улучшите статью в соответствии с правилами написания статей. Ольмеки название племени … Википедия
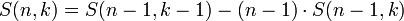 для 0 < k < n.
для 0 < k < n.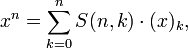 где
где 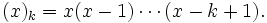
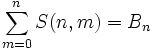 — число Белла.
— число Белла.