Парадокс дней рождения

Парадо́кс дней рожде́ния — это кажущееся парадоксальным утверждение, что вероятность совпадения дней рождения (числа и месяца) хотя бы у двух членов группы из 23 и более человек, превышает 50 %. С практической точки зрения это означает, что если, например, в вашем классе более 22 учеников, то более вероятно, что у кого-то из одноклассников дни рождения придутся на один день, чем что у каждого будет свой собственный день рождения.

Для 60 и более человек вероятность такого совпадения превышает 99 %, хотя 100 % она достигает, согласно принципу Дирихле, только когда в группе не менее 367 человек (с учётом високосных лет).

Такое утверждение может показаться неочевидным, так как вероятность совпадения дней рождения двух человек в любой день года (1/365 = 0,27 %), помноженная на число человек в группе из 23, даёт лишь 23/365 = 6,3 %. Это рассуждение неверно, так как число возможных пар (253) значительно превышает число человек в группе. Таким образом, утверждение не является парадоксом в строгом научном смысле — логического противоречия в нём нет, а парадокс заключается лишь в различиях между интуитивным восприятием ситуации человеком и результатами математического расчёта.

График, показывающий вероятность совпадения дней рождения хотя бы у двух человек из указанного числа людей

Интуитивное восприятие

Один из способов понять на интуитивном уровне, почему в группе из 23 человек вероятность совпадения дней рождения у двух человек столь высока, состоит в осознании следующего факта: поскольку рассматривается вероятность совпадения дней рождения у любых двух человек в группе, то эта вероятность определяется количеством пар людей, которые можно составить из 23 человек. Так как порядок людей в парах не имеет значения, то общее число таких пар равно числу сочетаний из 23 по 2, то есть (23 × 22)/2 = 253 пары. Посмотрев на это число, легко понять, что при рассмотрении 253 пар людей вероятность совпадения дней рождения хотя бы у одной пары будет достаточно высокой.

Ключевым моментом здесь является то, что утверждение парадокса дней рождения говорит именно о совпадении дней рождения у каких-либо двух членов группы. Одно из распространённых заблуждений состоит в том, что этот случай путают с другим — похожим, на первый взгляд, — случаем, когда из группы выбирается один человек и оценивается вероятность того, что у кого-либо из других членов группы день рождения совпадёт с днем рождения выбранного человека. В последнем случае вероятность совпадения значительно ниже.

Расчёт вероятности

В данном примере для расчёта вероятности того, что в группе из n человек как минимум у двух дни рождения совпадут, примем, что дни рождения распределены равномерно, то есть нет високосных лет, близнецов, рождаемость не зависит от дня недели, времени года и других факторов. В действительности, это не совсем так — обычно летом рождается больше детей; кроме того, в некоторых странах из-за особенностей работы больниц больше детей рождается в определённые дни недели. Однако неравномерность распределения может лишь увеличить вероятность совпадения дней рождения, но не уменьшить: если бы все люди рождались только в 3 дня из 365, то вероятность совпадения дней рождения была бы очень высокой.

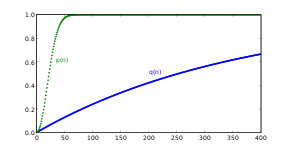
Рассчитаем сначала, какова вероятность p (n) того, что в группе из n человек дни рождения всех людей будут различными. Если n > 365, то в силу принципа Дирихле вероятность равна нулю. Если же n ≤ 365, то будем рассуждать следующим образом. Возьмём наугад одного человека из группы и запомним его день рождения. Затем возьмём наугад второго человека, при этом вероятность того, что у него день рождения не совпадёт с днем рождения первого человека, равна 1 — 1/365. Затем возьмём третьего человека, при этом вероятность того, что его день рождения не совпадёт с днями рождения первых двух, равна 1 — 2/365. Рассуждая по аналогии, мы дойдём до последнего человека, для которого вероятность несовпадения его дня рождения со всеми предыдущими будет равна 1 — (n — 1)/365. Перемножая все эти вероятности, получаем вероятность того, что все дни рождения в группе будут различными:

$\bar p(n) = 1 \cdot \left(1-\frac{1}{365}\right) \cdot \left(1-\frac{2}{365}\right) \cdots \left(1-\frac{n-1}{365}\right) = { 365 \cdot 364 \cdots (365-n+1) \over 365^n } = { 365! \over 365^n (365-n)!},$

Тогда вероятность того, что хотя бы у двух человек из n дни рождения совпадут, равна

$p(n) = 1 - \bar p(n) .$

Значение этой функции превосходит 1/2 при n = 23 (при этом вероятность совпадения равна примерно 50,7 %). Вероятности для некоторых значений n иллюстрируются следующей таблицей:

n	p (n)
10	12 %
20	41 %
30	70 %
50	97 %
100	99,99996 %
200	99,9999999999999999999999999998 %
300	(1 − 7×10−73) × 100 %
350	(1 − 3×10−131) × 100 %
367	100 %

Данную задачу можно переформулировать в терминах классической «задачи о совпадениях». Пусть урна содержит M(в данном случае 365) шаров, занумерованных числами 1,2,…M. Производится выборка с возвращением объёма n(в данном случае количество человек в группе), при этом рассматриваемые выборки считаются упорядоченными (то есть выборка 1,2,4,6 и 4,2,6,1 считаются различными). Требуется посчитать вероятность события, заключающегося в отсутствии повторений в выборке (все расчёты аналогичны приведённым выше).

Альтернативный метод

Вероятность совпадения дней рождения в группе можно также рассчитать с использованием формул комбинаторики. Представим, что каждый день года — это одна буква в алфавите из 365 букв. Дни рождения n человек могут быть представлены строкой, состоящей из n букв такого алфавита. Общее число таких строк равно

$n_\mathrm{total} = 365^{n}\,$

Общее число строк, в которых буквы не повторяются, составит

$n_\mathrm{unique} = \frac{365!}{(365-n)!}$

Тогда, если строки выбираются случайно (с равномерным распределением), то вероятность выбрать строку, в которой хотя бы две буквы совпадут, равна

$p(n) = 1 - \frac{n_\mathrm{unique}}{n_\mathrm{total}} = 1 - \frac{\frac{365!}{(365-n)!}}{365^{n}}$

для n ≤ 365 и p (n) = 1 для n > 365.

Поскольку

$\frac{\left(\frac{365!}{(365-n)!}\right)}{365^{n}}=\frac{365\cdot 364\cdot 363 \cdots (365-n+1)}{365^{n}}=$

$\frac{365}{365}\frac{364}{365}\frac{363}{365}\cdots \frac{365-n+1}{365}=1 \cdot \left(1-\frac{1}{365}\right) \cdot \left(1-\frac{2}{365}\right) \cdots \left(1-\frac{n-1}{365}\right) ,$

то это выражение эквивалентно представленному выше.

Аппроксимации

Используя разложение экспоненциальной функции в ряд Тейлора

$e^x = 1 + x + \frac{x^2}{2!}+\cdots$

приведённое выше выражение, дающее значение p (n), можно аппроксимировать следующим образом:

График, показывающий соотношение между точным значением и аппроксимацией p (n)

$\bar p(n) \approx 1 \cdot e^{-1/365} \cdot e^{-2/365} \cdots e^{-(n-1)/365}$

$= 1 \cdot e^{-(1+2+ \cdots +(n-1))/365}$

$= e^{-(n(n-1))/2 \cdot 365}$

Следовательно,

$p(n) = 1-\bar p(n) \approx 1 - e^{-(n(n-1))/2 \cdot 365}$

Для ещё более грубой аппроксимации можно взять выражение

$p(n)\approx 1-e^{-n^2/{2 \cdot 365}},\,$

которое, как показывает график, всё ещё даёт достаточную точность.

Приведём ещё одну аппроксимацию.

Вероятность того, что у двух людей день рождения не совпадает, равна 364/365. В группе из n человек C(n, 2) = n(n-1)/2 пар. Поэтому вероятность p (n) при условии независимости этих событий может быть приближена числом

$\left(\frac{364}{365}\right)^{C(n,2)}.$

Следовательно, получаем приближение для искомой вероятности p (n)

$p(n) \approx 1 - \left(\frac{364}{365}\right)^{C(n,2)}.$

Пуассоновское приближение

Используя приближение Пуассона для бинома, исходя из предыдущего приближения для p (n), получим чуть больше 50 %:

$\mathrm{Poi}\left(\frac{C(23, 2)}{365}\right) =\mathrm{Poi}\left(\frac{253}{365}\right) \approx \mathrm{Poi}(0.6932)$

$\Pr(X>0)=1-\Pr(X=0)=1-e^{-0.6932}=1-0.499998=0.500002.$

Подсчёт количества людей для 50 % вероятности

Используя предыдущую формулу для подсчёта p (n), мы можем выразить n, считая p (n) равной 50 %,получим

$n \approx \frac{1}{2} + \sqrt{\frac{1}{4} - 2 \times 365 \times \ln(0.5)} = 22.9999.$

Есть ещё один способ оценки n для 50 % вероятности. Как доказывалось выше

$1-p(n) = \bar p(n) = \prod_{k=1}^{n-1}\left(1-{k \over 365}\right) .$

Найдём наименьшее n,для которого p(n) > 1/2; или, что то же самое,p(n) < 1/2.

Используя разложение экспоненты в ряд Тейлора, получим 1 − x < e^−x. И следовательно,

$\bar p(n) = \prod_{k=1}^{n-1}\left(1-{k \over 365}\right) < \prod_{k=1}^{n-1}\left(e^{-k/365}\right) = e^{-(n(n-1))/(2\times 365)} .$

Так как p(n) < 1/2,

$e^{-(n(n-1))/(2\cdot 365)} < \frac{1}{2}$

Решая относительно n,получаем

$n^2-n > 2\times365\ln 2 \,\! .$

Отсюда находим n равно 23.

Родившиеся в один день с заданным человеком

Сравнение вероятностей p (n) и q (n)

Интересно сравнить вероятность p (n) с вероятностью того, что в группе из n человек у кого-либо день рождения совпадет с днём рождения некоторого заранее выбранного человека (не принадлежащего к этой группе). Эта вероятность равна

$q(n) = 1 - \left( \frac{365-1}{365} \right)^n$

Подставляя n = 23, получаем q (n) примерно 5,9 %, что лишь немногим лучше одного шанса из 17. Для того, чтобы вероятность совпадения дня рождения с заданным человеком превысила 50 %, число людей в группе должно быть не менее 253. Это число заметно больше, чем половина дней в году (365/2 = 182.5); так происходит из-за того, что у остальных членов группы дни рождения могут совпадать между собой, и это уменьшает вероятность совпадения одного из них с днём рождения заданного человека.

Обобщения

Совпадение дискретных случайных величин

Задача, представленная парадоксом дней рождения, может быть поставлена в общем виде следующим образом: если даны n равномерно распределённых случайных чисел в диапазоне от 1 до d, то какова вероятность p (n ; d) того, что хотя бы два из этих чисел совпадут?

Рассуждая таким же образом, как описано выше, можно получить общие решения:

$p(n;d) = \begin{cases} 1-\prod_{k=1}^{n-1}\left(1-{k \over d}\right) & n\le d \\ 1 & n > d \end{cases}$

$p(n;d) \approx 1 - e^{-(n(n-1))/2d}$

$q(n;d) = 1 - \left( \frac{d-1}{d} \right)^n$

И наоборот, если n(p;d) обозначает количество чисел, принимающих значения от 1 до d,для которого вероятность того, что хотя бы 2 из них совпадают равно p,то

$n(p;d)\approx \sqrt{2d \cdot \ln\left({1 \over 1-p}\right)}$.

Несколько типов людей

Выше парадокс дней рождения был представлен для одного «типа» людей. Можно обобщить задачу, введя несколько «типов», например, разделив людей на мужчин (m) и женщин (n). Подсчитаем вероятность того, что хотя бы у одной женщины и у одного мужчины совпадают дни рождения (совпадение дней рождения у двух женщин или у двух мужчин не учитываются):

$p_0 =1 - \frac{1}{d^{m+n}} \sum_{i=1}^m \sum_{j=1}^n S_2(m,i) S_2(n,j) \prod_{k=0}^{i+j-1} (d - k)$

где d = 365 и S₂() — числа Стирлинга второго рода. Интересно, что нет однозначного ответа на вопрос о величине n+m для заданной вероятности. Например, вероятность 0,5 даёт как набор из 16 мужчин и 16 женщин, так и набор из 43 мужчин и 6 женщин.

Близкие дни рождения

Другое обобщение парадокса дней рождения состоит в постановке задачи о том, сколько человек нужно для того, чтобы вероятность наличия в группе людей, дни рождения которых различаются не более чем на один день (или на два, три дня и так далее), превысила 50 %. Эта задача более сложная, при её решении используется принцип включения-исключения. Результат (опять-таки в предположении, что дни рождения распределены равномерно) получается следующим:

Максимальное различие дней рождения, дней	Необходимое число людей
1	23
2	14
3	11
4	9
5	8
6	8
7	7
8	7

Таким образом, вероятность того, что даже в группе из 7 людей дни рождения хотя бы у двух будут различаться не более чем на неделю, превышает 50 %.

Приложения

Парадокс дней рождения в общем смысле применим к хеш-функциям: если хеш-функция генерирует N-битное значение, то число случайных входных данных, для которых хеш-коды с большой вероятностью дадут коллизию (то есть найдутся равные хеш-коды, полученные на разных входных данных), равно не 2^N, а только около 2^N/2. Это наблюдение используется в атаке «дней рождения» на криптографические хеш-функции.

N	количество различных выходных цепочек (2^N)	Вероятность хотя бы одной коллизии (p)
		10−18	10−15	10−12	10−9	10−6	0,1 %	1 %	25 %	50 %	75 %
32	4,3 × 109	2	2	2	2.9	93	2.9 × 10³	9.3 × 10³	5.0 × 104	7.7 × 104	1.1 × 105
64	1,8 × 1019	6.1	1.9 × 10²	6.1 × 10³	1.9 × 105	6.1 × 106	1.9 × 108	6.1 × 108	3.3 × 109	5.1 × 109	7.2 × 109
128	3,4 × 1038	2.6 × 1010	8.2 × 1011	2.6 × 1013	8.2 × 1014	2.6 × 1016	8.3 × 1017	2.6 × 1018	1.4 × 1019	2.2 × 1019	3.1 × 1019
256	1,2 × 1077	4.8 × 1029	1.5 × 1031	4.8 × 1032	1.5 × 1034	4.8 × 1035	1.5 × 1037	4.8 × 1037	2.6 × 1038	4.0 × 1038	5.7 × 1038
384	3,9 × 10115	8.9 × 1048	2.8 × 1050	8.9 × 1051	2.8 × 1053	8.9 × 1054	2.8 × 1056	8.9 × 1056	4.8 × 1057	7.4 × 1057	1.0 × 1058
512	1,3 × 10154	1.6 × 1068	5.2 × 1069	1.6 × 1071	5.2 × 1072	1.6 × 1074	5.2 × 1075	1.6 × 1076	8.8 × 1076	1.4 × 1077	1.9 × 1077

В белых квадратах написано количество входных данных(количество человек в группе), при котором коллизия будет с заданной вероятностью(проводя аналогию с парадоксом, кол-во различных выходных цепочек равно 365).

Сходный математический аппарат используется для оценки популяции рыб в озёрах методом «capture-recapture». Действительно, если каждую пойманную рыбу помечать и отпускать, то вероятность поймать помеченную рыбу будет расти нелинейно (в соответствии с приведённым выше графиком) с ростом количества попыток. Размер популяции грубо может быть оценен как квадрат числа попыток до первой помеченной пойманной рыбы.

Решение задачи в общем виде находит применение во многих разделах математики, например в недетерминированных алгоритмах факторизации. Так, одно из самых простых объяснений ρ-метода Полларда аналогично объяснению парадокса дней рождения: достаточно иметь примерно $\sqrt{p}$ случайных чисел от 0 до $n=p q ~$, где $p < q ~$ — простые, чтобы хотя бы для одной из пар чисел с высокой вероятностью нашёлся $\gcd \left( |x-y|,n \right) > 1$, который и будет делителем числа n.

Обратные задачи

1) Поиск наименьшего n,для которого вероятность p(n) больше заданного p.

2) Поиск наибольшего n,для которого вероятность p(n) меньше заданного p.

Пользуясь выше приведённой формулой, получаем

$n(p;365)\approx \sqrt{2\times 365\ln\left({1 \over 1-p}\right)}.$

p	n	n↓	p(n↓)	n↑	p(n↑)
0.01	0.14178√365 = 2.70864	2	0.00274	3	0.00820
0.05	0.32029√365 = 6.11916	6	0.04046	7	0.05624
0.1	0.45904√365 = 8.77002	8	0.07434	9	0.09462
0.2	0.66805√365 = 12.76302	12	0.16702	13	0.19441
0.3	0.84460√365 = 16.13607	16	0.28360	17	0.31501
0.5	1.17741√365 = 22.49439	22	0.47570	23	0.50730
0.7	1.55176√365 = 29.64625	29	0.68097	30	0.70632
0.8	1.79412√365 = 34.27666	34	0.79532	35	0.81438
0.9	2.14597√365 = 40.99862	40	0.89123	41	0.90315
0.95	2.44775√365 = 46.76414	46	0.94825	47	0.95477
0.99	3.03485√365 = 57.98081	57	0.99012	58	0.99166

Наилучшая позиция

Пусть в комнате находятся n-1 человек, и дни рождения всех присутствующих в комнате различны. Назовём g(n) вероятность того, что день рождения вошедшего человека совпадает с кем-нибудь из присутствующих в комнате. Требуется найти n, для которого g(n) максимально. Задача сводится к нахождению максимального значения p(n)-p(n-1). Пользуясь выше приведённой формулой для p(n), получаем n=20.

Среднее число людей

Вернёмся к альтернативной проблеме. Сколько в среднем нужно людей для того, чтобы хотя бы у двух из них совпали дни рождения?

Эта проблема имела отношение к алгоритмам хеширования и была исследована Дональдом Кнутом. Оказывается, что для задачи в общем виде интересующая нас случайная величина имеет математическое ожидание равное

$\scriptstyle\overline{n}\,=\,1+Q(M)$, где

$Q(M)=\sum_{k=1}^{M} \frac{M!}{(M-k)! M^k}.$

Функция

$Q(M)= 1 + \frac{M-1}{M} + \frac{(M-1)(M-2)}{M^2} + \cdots + \frac{(M-1)(M-2) \cdots 1}{M^{M-1}}$

была исследована Сриниваса Рамануджаном Айенгором, который получил для неё асимптотическое разложение:

$Q(M)\sim\sqrt{\frac{\pi M}{2}}-\frac{1}{3}+\frac{1}{12}\sqrt{\frac{\pi}{2M}}-\frac{4}{135M}+\cdots.$

при M = 365 имеем среднее число людей равное $\scriptstyle\overline{n}\,=\,1+Q(M)\approx 24.61658$, немного больше чем число людей, обеспечивающих 50 % вероятность. Как ни удивительно, необходимое число людей равно M + 1 = 366 (у 365 людей дни могут распределиться по каждому из 365 дней года без совпадений), хотя в среднем нужно лишь 25.

См. также

• Задача о письмах
• Синхронность

Ссылки

• Парадоксы теории вероятностей
• Парадокс дней рождения и стойкость криптографии
• Парадокс дней рождения  (англ.)

Литература

• John G. Kemeny, J. Laurie Snell, and Gerald Thompson Introduction to Finite Mathematics . The first edition, 1957.(русский перевод: Кемени Дж., Снелл Дж., Томпсон Дж. Введение в конечную математику. Издательство иностранной литературы, 1963 г., 488 стр.)
• Секей Г. Парадоксы в теории вероятностей и математической статистике. РХД, 2003. (ISBN 5-93972-150-8)
• Козлов М. В. Элементы теории вероятностей в примерах и задачах. МГУ, 1990. (ISBN 5-211-00312-8)
• Ширяев А. Н. Вероятность-1. МЦНМО, 2007. (ISBN 987-5-94057-036-3)
• Goldberg S. A Direct Attack on a Birthday Problem (англ.) // Mathematical Mathematics Magazine. — May 1976. — В. 49. — С. 130-132.
• Mosteller F. Understanding the Birthday Problem (англ.) // The Mathematics Teacher. — May 1962. — С. 322-325.
• Eurobirthdays 2012 года.День рождения проблемы. Практический пример футбольного дня рождения парадокс. (английская версия)

В данной статье или разделе имеется список источников или внешних ссылок, но источники отдельных утверждений остаются неясными из-за отсутствия сносок. Вы можете улучшить статью, внеся более точные указания на источники.