Числа стирлинга второго рода
- Числа стирлинга второго рода
-
В комбинаторике числом Стирлинга второго рода S(n, k) называется число неупорядоченных разбиений n-элементного множества на k непустых подмножеств.
Числа Стирлинга второго рода задаются рекуррентным соотношением:
S(n,n) = 1, для n ≥ 0,
S(n,0) = 0, для n > 0,
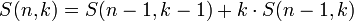 для 0 < k < n.
для 0 < k < n.
Пример
Первые ряды:
|
0 |
1 |
2 |
3 |
4 |
5 |
6 |
| 0 |
1 |
|
|
|
|
|
|
| 1 |
0 |
1 |
|
|
|
|
|
| 2 |
0 |
1 |
1 |
|
|
|
|
| 3 |
0 |
1 |
3 |
1 |
|
|
|
| 4 |
0 |
1 |
7 |
6 |
1 |
|
|
| 5 |
0 |
1 |
15 |
25 |
10 |
1 |
|
| 6 |
0 |
1 |
31 |
90 |
65 |
15 |
1 |
Свойства
Программы для расчета
Delphi
type
TTwoDimArray = array of array of Double;
procedure GetStirlingNumbers(n_max, m_max: Integer; var StirlingNumbers: TTwoDimArray);
var
I, J: Integer;
begin
{ Выделение памяти под массив чисел }
SetLength(StirlingNumbers, n_max+1, m_max+1);
{ Заполнение массива }
{ S(n,0) = 0 }
for I := 0 to n_max do
StirlingNumbers[I, 0] := 0;
{ S(n,n) = 1 }
for I := 0 to n_max do
StirlingNumbers[I, I] := 1;
{ S(n,m) = S(n-1,m-1) + m*S(n-1,m) }
for I := 1 to n_max do
for J := 1 to I-1 do
StirlingNumbers[I, J] := StirlingNumbers[I-1, J-1] + J * StirlingNumbers[I-1, J];
end;
C#
void GetStirlingNumbers(int n_max, int m_max, double[,] StirlingNumbers)
{
// Выделение памяти под массив чисел
StirlingNumbers = new double [n_max+1, m_max+1];
// Заполнение массива
// S(n,0) = 0
for (int i = 0; i < n_max; i++)
StirlingNumbers[i, 0] = 0;
// S(n,n) = 1
for (int i = 0; i < n_max; i++)
StirlingNumbers[i, i] = 1;
// S(n,m) = S(n-1,m-1) + m*S(n-1,m)
for (int i = 1; i < n_max; i++)
for (int j = 1; j < i-1; j++)
StirlingNumbers[i, j] = StirlingNumbers[i-1, j-1] + j * StirlingNumbers[i-1, j];
}
Смотри также
Ссылки
Wikimedia Foundation.
2010.
Полезное
Смотреть что такое "Числа стирлинга второго рода" в других словарях:
Числа Стирлинга второго рода — В комбинаторике числом Стирлинга второго рода из n по k, обозначаемым или , называется количество неупорядоченных разбиений n элементного множества на k непустых подмножеств. Содержание 1 Рекуррентная формула … Википедия
Числа Стирлинга первого рода — (без знака) количество перестановок порядка n с k циклами. Содержание 1 Определение 2 Рекуррентное соотношение 3 … Википедия
Число Стирлинга второго рода — В комбинаторике числом Стирлинга второго рода S(n, k) называется число неупорядоченных разбиений n элементного множества на k непустых подмножеств. Числа Стирлинга второго рода задаются рекуррентным соотношением: S(n,n) = 1, для n ≥ 0, S(n,0) = 0 … Википедия
Числа Стирлинга — комбинаторные понятия, введенные Джеймсом Стирлингом в середине XVIII века. Числа Стирлинга первого рода Числа Стирлинга второго рода Литература Белешко Д. Комбинаторика (часть 2). СПбГУ ИТМО. Иванов Б. Н. Дискретная математика. М.:ЛБЗ, 2001.… … Википедия
Число Стирлинга первого рода — Числа Стирлинга первого рода количество перестановок из n предметов, имеющие ровно k циклов. Содержание 1 Определение 2 Рекуррентное соотношение 3 Пример 4 Свойст … Википедия
Числа Белла — В комбинаторике числом Белла называется число всех неупорядоченных разбиений n элементного множества, при этом по определению полагают . Численные значения Значения чисел Белла для образуют последовательность: 1, 1, 2, 5, 15, 52, 203, 877, 4140,… … Википедия
Парадокс дней рождения — Парадокс дней рождения это кажущееся парадоксальным утверждение, что вероятность совпадения дней рождения (числа и месяца) хотя бы у двух членов группы из 23 и более человек, превышает 50 %. С практической точки зрения это означает,… … Википедия
ГАММА-ФУНКЦИЯ, — Г функция, трансцендентная функция , распространяющая значения факториала на случай любого комплексного Г. ф. введена Л. Эйлером [(L. Euler), 1729, письмо к X. Гольдбаху (Ch. Goldbach)] при помощи бесконечного произведения иа к рого Л. Эйлер… … Математическая энциклопедия
Природный газ — (Natural gas) Природный газ это один из самых распространенных энергоносителей Определение и применение газа, физические и химические свойства природного газа Содержание >>>>>>>>>>>>>>> … Энциклопедия инвестора
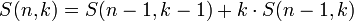 для 0 < k < n.
для 0 < k < n.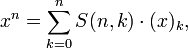 где
где 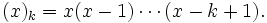
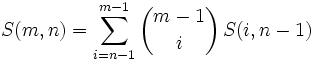
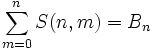 — число Белла.
— число Белла.