Число Серпинского

В теории чисел нечётное натуральное число k является числом Серпинского, если для любого n число 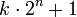$k\cdot 2^n+1$ является составным. Соответственно, чтобы доказать, что число k не является числом Серпинского нужно найти такое n, что число 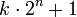$k\cdot 2^n+1$ является простым. Числа Серпинского названы так в честь открывшего их польского математика Вацлава Серпинского.

Существование чисел Серпинского довольно неочевидно. Например, если рассмотреть последовательность 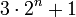$3 \cdot 2^n+1$, то в ней регулярно будут встречаться простые числа, и неожиданным является тот факт, что для некоторых k в последовательности 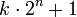$k\cdot 2^n+1$ никогда не встретится простое число.

Проблема Серпинского

Задача отыскания минимального числа Серпинского известна как проблема Серпинского.

В 1962 году Джон Селфридж доказал, что 78557 — число Серпинского. А именно, он показал, что каждое число вида 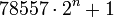$78557\cdot 2^n+1$ делится по крайней мере на одно число из множества {3, 5, 7, 13, 19, 37, 73}. Аналогично доказывается, что 271129 также является числом Серпинского: каждое число вида 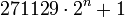$271129\cdot 2^n+1$ делится по крайней мере на одно число из множества {3, 5, 7, 13, 17, 241}.

В 1967 году Селфридж и Серпинский предположили, что 78557 является наименьшим числом Серпинского. Доказательством этой гипотезы занимается проект распределённых вычислений Seventeen or Bust.

Ссылки

• Prime Riddle(англ.) — статья про числа Серпинского и проект Seventeen or Bust.