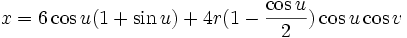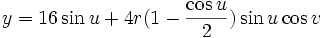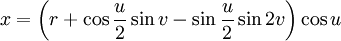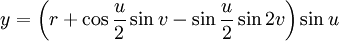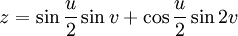Поверхность Клейна

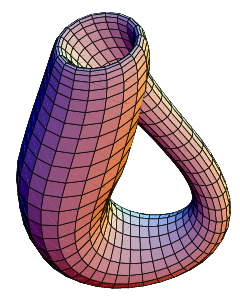Бутылка Клейна, погружённая в трёхмерное пространство.

Бутылка Клейна — это определённая неориентируемая поверхность (то есть двумерное многообразие). Бутылка Клейна впервые была описана в 1882 г. немецким математиком Ф. Клейном. Она тесно связана с лентой Мёбиуса и проективной плоскостью. Название, по-видимому, происходит от неправильного перевода немецкого слова Fläche (поверхность), которое в немецком языке близко по написанию к слову Flasche (бутылка).

Чтобы построить модель бутылки Клейна, необходимо взять бутылку с двумя отверстиями: в донышке и в стенке, вытянуть горлышко, изогнуть его вниз, и продев его через отверстие в стенке бутылки (для настоящей бутылки Клейна в четырёхмерном пространстве это отверстие не нужно, но без него нельзя обойтись в трёхмерном евклидовом пространстве), присоединить к отверстию на дне бутылки.

В отличие от обыкновенного стакана у этого объекта нет «края», где бы поверхность резко заканчивалась. В отличие от воздушного шара можно пройти путь изнутри наружу не пересекая поверхность (то есть на самом деле у этого объекта нет «внутри» и нет «снаружи»).

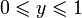Более формально, бутылку Клейна можно получить склеиванием квадрата $[0,1]\times [0,1]$ идентифицируя точки (0,y) ~ (1,y) при $0\leqslant y\leqslant 1$ и (x,0) ~ (1-x,1) при 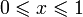$0\leqslant x \leqslant 1$, как показано на диаграмме.

Свойства

• Подобно ленте Мёбиуса, бутылка Клейна является двумерным дифференцируемым неориентируемым многообразием. В отличие от ленты Мёбиуса, бутылка Клейна является замкнутым многообразием, то есть компактным многообразием без края.
• Бутылка Клейна не может быть вложена (только погружена) в трёхмерное евклидово пространство 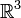$\R^3$, но вкладывается в $\R^4$.
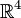• Бутылка Клейна может быть получена склеиванием двух лент Мёбиуса по краю. Однако в обычном трехмерном евклидовом пространстве 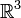$\R^3$ сделать это, не создав самопересечения, невозожно.
• Хроматическое число поверхности равно 6.

Рассечения

При рассечении бутылки Клейна получается лента Мёбиуса

Реализация бутылки Клейна в виде восьмерки

Если разрезать бутылку Клейна пополам вдоль её оси симметрии, то результатом будет лента Мёбиуса, изображенная справа (необходимо помнить, что изображенного пересечения на самом деле нет).

Параметризация

Классическая параметризация Бутылки Клейна:

При $0\le\;u\le\;\pi\;$

$x=6\cos u(1+\sin u)+4r(1-\frac{\cos u}{2})\cos u\cos v$

$y=16\sin u+4r(1-\frac{\cos u}{2})\sin u\cos v$

$z=4r(1-\frac{\cos u}{2})\sin v$

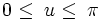
При $\pi\ \le\;u\le\;2\pi\;$

$x=6\cos u(1+\sin u)-4r(1-\frac{\cos u}{2})\cos v$

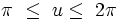
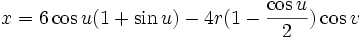
y = 16sinu

$z=4r(1-\frac{\cos u}{2})\sin v$

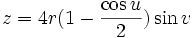
Бутылка Клейна в виде восьмёрки имеет довольно простую параметризацию:

$x = \left(r + \cos\frac{u}{2}\sin v - \sin\frac{u}{2}\sin 2v\right) \cos u$

$y = \left(r + \cos\frac{u}{2}\sin v - \sin\frac{u}{2}\sin 2v\right) \sin u$

$z = \sin\frac{u}{2}\sin v + \cos\frac{u}{2}\sin 2v$

В этом виде самопересечение имеет форму геометрического круга в плоскости XY. Константа r равна радиусу круга. Параметр u задаёт угол на плоскости XY и v обозначает положение около 8-образного сечения.

Бутылка Клейна в культуре

Стеклянная бутылка Клейна

• Изредка встречается сувенир в виде стеклянной бутылки Клейна. Для изготовления такой бутылки нужен стеклодув высокой квалификации. В том месте, где бутылка пересекает сама себя, по технологическим причинам приходится оставлять отверстие.
• В сериале Футурама в серии «The Route of All Evil» на полке показано пиво Klein’s, которое разлито в бутылки Клейна.

См. также

• Топология
• Алгебраическая топология
• Поверхность
• Лист Мебиуса

Ссылки

• Топология для школьников
• Бутылка Клейна своими руками
• Магазин стеклянных бутылок Клейна