Энтропийная размерность

Размерность Минковского ограниченного множества в метрическом пространстве равна

$\lim\limits_{\epsilon\to0}\frac{\ln(N_\epsilon)}{-\ln(\epsilon)}$,

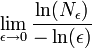где N_ε — минимальное число множеств диаметра ε, которыми можно покрыть наше множество. Если предел не существует, то можно рассматривать верхний и нижний предел и говорить соответственно о верхней и нижней размерности Минковского.

Близким к размерности Минковского понятием является размерность Хаусдорфа. Во многих случаях эти размерности совпадают, хотя существуют множества, для которых они различны.

Примеры

• размерность конечного множества равна нулю, так как для него ρ(n) не превосходит количества элементов в нем.
• размерность отрезка равна 1, так как необходимо 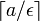$\lceil a/\epsilon\rceil$ отрезков длины ε, чтобы покрыть отрезок длины a. Таким образом,

  $\lim\limits_{\epsilon\to0}\frac{\ln(N_\epsilon)}{-\ln(\epsilon)}=\lim\limits_{\epsilon\to0}\frac{\ln a-\ln\epsilon}{-\ln\epsilon}=1$,

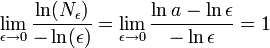• размерность квадрата равна 2, так как число квадратиков с диагональю 1 / n, необходимых, чтобы покрыть квадрат со стороной a, ведет себя примерно как a²n².
• размерность фрактального множества может быть дробным числом. Так, размерность кривой Коха равна ln4 / ln3.

Более подробно  

Неформальное рассуждение, показывающее это, таково. Отрезок можно разбить на 2 части, подобные исходному отрезку с коэффициентом 1/2. Чтобы покрыть отрезок множествами диаметра 1 / n, нужно покрыть каждую из половин такими множествами. Но для половины их нужно столько же, сколько для всего отрезка множеств диаметра 2 / n. Поэтому для отрезка имеем 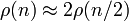$\rho(n)\approx 2\rho(n/2)$. То есть, при увеличении n в два раза ρ(n) увеличивается тоже в два раза. Иными словами, ρ(n) — линейная функция.

Для квадрата аналогичное рассуждение дает 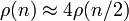$\rho(n)\approx 4\rho(n/2)$. То есть, при увеличении n в два раза ρ(n) увеличивается в 4 раза. Иными словами, ρ(n) — квадратичная функция.

Наконец, кривая Коха состоит из 4 частей, каждая из которых подобна исходной кривой с коэффициентом 1/3. Поэтому для неё 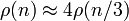$\rho(n)\approx 4\rho(n/3)$. Подставляя n = 3^k, получаем 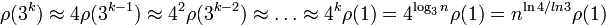$\rho(3^k)\approx 4\rho(3^{k-1})\approx 4^2\rho(3^{k-2})\approx \dots\approx 4^k\rho(1)=4^{\log_3 n}\rho(1)=n^{\ln4/ln3}\rho(1)$. Отсюда следует, что размерность равна ln4 / ln3.

Формально: пусть n - шаг фрактала, на n-ом шаге у нас будет 4ⁿ равных отрезков, длиной 3 ^{− n}. Возьмём за ε отрезок длиной 3 ^{− n}, тогда чтобы покрыть всю кривую Коха, нам понадобится 4ⁿ отрезков. Для того, чтобы выполнялось условие ε→0, устремим n→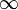$\infty$. Получим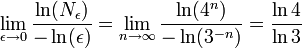

  $\lim\limits_{\epsilon\to0}\frac{\ln(N_\epsilon)}{-\ln(\epsilon)}=\lim\limits_{n\to\infty}\frac{\ln(4^{n})}{-\ln(3^{-n})}=\frac{\ln4}{\ln3}$

• размерность Минковского множества 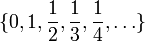$\{0,1,\frac12,\frac13,\frac14,\dots\}$ равна 1/2.

Свойства

• Размерность Минковского конечного объединения множеств равна максимуму из их размерностей. В отличие от размерности Хаусдорфа, это неверно для счётного объединения. Например, множество рациональных чисел между 0 и 1 имеет размерность Минковского 1, хотя является счётным объединением одноэлементных множеств (размерность каждого из которых равна 0). Пример замкнутого счётного множества с ненулевой размерностью Минковского приведён выше.
• Нижняя размерность Минковского любого множества больше либо равна его размерности Хаусдорфа.
• Размерность Минковского любого множества равна размерности Минковского его замыкания. Поэтому имеет смысл говорить лишь о размерностях Минковского замкнутых множеств.

См. также

• Размерность Хаусдорфа
• фрактал