- ЭРГОДИЧЕСКАЯ ТЕОРИЯ
- ЭРГОДИЧЕСКАЯ ТЕОРИЯ
-
Введение
Э. т. (метрическая теория динамических систем) - раздел теории динамических систем, изучающий их статистич. свойства. Возникновение Э. т. (1-я треть 20 в.) было стимулировано попытками доказать эргодическую гипотезу (термин введён П. и Т. Эренфестами, Р. и Т. Ehrenfest), предложенную в кон. 19 в. Л. Больцманом для обоснования статистич. физики.
В Э. т. осн. объект исследования-динамич. система (ДС), понимаемая как группа (или полугруппа) преобразований нек-рого пространства с мерой, сохраняющих эту меру. В применении к консервативным ДС, описываемым дифференц. ур-ниями, речь идёт о семействе сдвигов вдоль фазовых траекторий, а роль сохраняющейся (инвариантной) меры играет фазовый объём. В общем случае пространство с мерой - это тройка (X,
 , m), в к-рой X- произвольное множество с выделенным семейством
, m), в к-рой X- произвольное множество с выделенным семейством 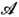 его подмножеств (s-алгеброй измеримых подмножеств), содержащим само X в . качестве одного из элементов и замкнутым относительно теоретико-множественных операций (объединения и пересечения конечного или счётного числа множеств и перехода от любого множества к его дополнению). М е р а m - это неотрицательная ф-ция, заданная на
его подмножеств (s-алгеброй измеримых подмножеств), содержащим само X в . качестве одного из элементов и замкнутым относительно теоретико-множественных операций (объединения и пересечения конечного или счётного числа множеств и перехода от любого множества к его дополнению). М е р а m - это неотрицательная ф-ция, заданная на  и обладающая свойством счётной аддитивности: если А1, А2, ...- множества из
и обладающая свойством счётной аддитивности: если А1, А2, ...- множества из  , к-рые попарно не пересекаются, то мера их объединения равна сумме мер. Если m( Х)<
, к-рые попарно не пересекаются, то мера их объединения равна сумме мер. Если m( Х)<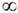 , то m можно нормировать, поделив на m(X), и считать (X,
, то m можно нормировать, поделив на m(X), и считать (X,  , m) вероятностным пространством (см. Вероятностей теория). Для ДС, отвечающей гамильтоно-вой системе дифференциальных ур-ний, в качестве X можно взять любую гиперповерхность постоянной энергии, а в качестве m - меру, индуцированную на этой гиперповерхности фазовым объёмом. Всюду в дальнейшем предполагается, что рассматриваемые ДС определены на вероятностном пространстве.
, m) вероятностным пространством (см. Вероятностей теория). Для ДС, отвечающей гамильтоно-вой системе дифференциальных ур-ний, в качестве X можно взять любую гиперповерхность постоянной энергии, а в качестве m - меру, индуцированную на этой гиперповерхности фазовым объёмом. Всюду в дальнейшем предполагается, что рассматриваемые ДС определены на вероятностном пространстве.
В большинстве случаев преобразования, входящие в ДС, образуют однопараметрич. группу {Tt}. Параметр t, интерпретируемый как время, обычно принимает любые действительные или любые целые значения. В первом случае говорят о ДС с непрерывным временем (п о т о к е), во втором - о ДС с дискретным временем (к а с к а д е). Иногда t принимает лишь неотрицат. значения и {Т t} является не группой, а полугруппой преобразований. (В этом случае иногда употребляют термины "п о л у п о т о к" и "п о л ук а с к а д".) Групповое свойство системы {Т t} выражается тождеством Т t T sx = T t+sx, справедливым для любого х
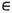 X и любых двух значений параметра. Вследствие группового свойства каскад {Т t} полностью определяется преобразованием Т=Т1 и часто отождествляется с ним. И н в а р иа н т н о с т ь м е р ы m означает, что для любого множества
X и любых двух значений параметра. Вследствие группового свойства каскад {Т t} полностью определяется преобразованием Т=Т1 и часто отождествляется с ним. И н в а р иа н т н о с т ь м е р ы m означает, что для любого множества 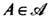 и любого t>=0выполняется равенство m( Т -t А)= = m(A), где Т -t А = (Т t)-1 А = {х
и любого t>=0выполняется равенство m( Т -t А)= = m(A), где Т -t А = (Т t)-1 А = {х 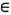 Х:Т t х
Х:Т t х 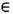 А} - полный прообраз множества А при отображении Т t.
А} - полный прообраз множества А при отображении Т t.
Следует отметить, что нек-рые ситуации, изучаемые в Э. т., не охватываются изложенной схемой. Это, в частности, относится к "некоммутативной эргодич. теории", связанной с квантовой физикой (см. ниже), и к тем задачам, в к-рых инвариантная мера не задана с самого начала, а может принадлежать нек-рому классу мер или выбирается из этого класса на основе тех или иных общих принципов. Кроме того, начиная с 70-х гг. в Э. т. постоянно растёт интерес к ДС, в к-рых временной параметр t пробегает не одномерное пространство R1 (или решётку Z1), а пространство Rd (решётку Zd) или группу ещё более общего вида. Такие системы находят, в частности, применение в статистич. физике. На них перенесена значит. часть "одномерной" Э. т., но с ними связан и ряд новых проблем.
Простейшими примерами ДС могут служить каскад и поток, определяемые одной и той же ф-лой Т t х =Fr( х + ta), где х - точка n -мерного единичного куба Х=К n=[0,1)n, п>1;a - векторный параметр, a Fr(x+ta) = x + ta -[x + ta]- вектор, состоящий из дробных частей компонент вектора х+ta (из каждой компоненты xi + tai вычтена её целая часть [ х i + tai]). В качестве инвариантной меры берётся n -мерный объём (м е р а Л еб е г а). Отождествляя К n с n -мерным тором (при п=1-с окружностью), говорят, что ДС порождена сдвигами на торе (поворотами окружности). Траектории этой системы образуют обмотку тора (рис. 1, на к-ром n= 2), причём либо все траектории замкнуты, либо все не замкнуты. Такая ДС возникает на каждом из инвариантных торов, на к-рые разбивается фазовое пространство гамильтоновой системы в случае, когда она вполне интегрируема.

Рис. 1. Отрезок траектории обмотки двумерного тора.
Другая ДС (каскад) {Т t} с тем же фазовым пространством определяется ф-лой T1x =Fr(Ax), где А - произвольная квадратная матрица n -го порядка с целочисленными элементами и определителем, равным +1 (условия, наложенные на А, гарантируют взаимную однозначность Т1. и инвариантность меры Лебега). Преобразование Т1 наз. а в т о м о р ф и з м о м т о р а.
Ещё один пример: преобразование единичного квадрата Х={(х1, х2):0<= х1, х2<=1} с мерой Лебега, к-рое можно задать равенством
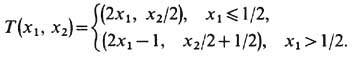
Его наз. п р е о б р а з о в а н и е м п е к а р я, что объясняется след. наглядной аналогией (рис. 2): прямоугольник A = {(x1, х2):0<=x1<=1/2, 0<= х2<=1} (левая половина первоначального куска теста) вдвое сжимается в вертикальном направлении и вдвое растягивается (раскатывается) в горизонтальном. В результате он принимает вид ТА. То же самое происходит и с прямоугольником В, но его нужно ещё сдвинуть, чтобы получить ТВ. Дальнейшие примеры ДС см. в последующих разделах статьи.

Рис. 2. Действие преобразования пекаря на левую и правую половину квадрата.
В Э. т. важную роль играет понятие и з о м о р ф и з м а ДС. Системы {Т t1} и {Т t2} изоморфны, если между их фазовыми пространствами (из к-рых, быть может, предварительно выброшено по множеству нулевой меры) можно установить взаимно-однозначное соответствие, сохраняющее структуру этих пространств, т. е. переводящее измеримые множества в измеримые множества той же меры, а каждое преобразование Т t1- в преобразование Т t2. Изоморфизм сохраняет все свойства ДС, существенные для Э. т., и с общей точки зрения изоморфные системы следует считать лишь разл. представлениями одного и того же объекта.
В "общей" Э. т. можно выделить ряд направлений, занимающихся изучением тех или иных свойств ДС. Так, с п е к т р а л ь н а я т е о р и я ДС применяет методы функционального анализа для изучения семейства линейных операторов {U t}, порождённого ДС. Эти операторы действуют по ф-ле (U tf)(х)=f(Т t х )в гильбертовом пространстве L2 = L2(X,
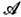 ,m), состоящем из комплекснозначных ф-ций f( х), х
,m), состоящем из комплекснозначных ф-ций f( х), х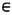 X, с интегрируемым по мере m квадратом модуля. Другое направление - э н т р о п и й н а я т е о р и я ДС - основано на тесной связи Э. т. с теорией вероятностей и на применении теоретико-вероятностных и теорети-ко-информац. идей. В "прикладной" Э. т. существуют разделы, в к-рых по преимуществу изучаются ДС, возникающие в теории вероятностей, дифференц. геометрии, теории чисел, статистич. физике и др. областях математики и физики (впрочем, мн. системы имеют "смешанное" происхождение, а вследствие изоморфизма само представление о происхождении ДС становится весьма условным).
X, с интегрируемым по мере m квадратом модуля. Другое направление - э н т р о п и й н а я т е о р и я ДС - основано на тесной связи Э. т. с теорией вероятностей и на применении теоретико-вероятностных и теорети-ко-информац. идей. В "прикладной" Э. т. существуют разделы, в к-рых по преимуществу изучаются ДС, возникающие в теории вероятностей, дифференц. геометрии, теории чисел, статистич. физике и др. областях математики и физики (впрочем, мн. системы имеют "смешанное" происхождение, а вследствие изоморфизма само представление о происхождении ДС становится весьма условным).
Проблема инвариантной меры
В приведённом выше определении ДС инвариантная мера играет не меньшую роль, чем сама группа преобразований: замена меры может резко изменить свойства системы. Если задано лишь нек-рое семейство преобразований пространства X, то возникает вопрос о существовании хотя бы одной, прежде всего вероятностной, инвариантной меры. Иногда он решается относительно просто. Так, по теореме Крылова - Боголюбова всякое непрерывное преобразование компактного метрич. пространства обладает вероятностной инвариантной мерой, а по Лиувилля теореме мера Лебега (фазовый объём) инвариантна относительно любой гамильтоновой системы (хотя, в последнем случае мера всего пространства бесконечна, на гиперповерхности постоянной энергии может индуцироваться конечная мера). Иногда вероятностная инвариантная мера единственна. Это имеет место, напр., для каскада, порождённого поворотом окружности: Т1 х =Fr( х +a), где a - иррациональное число. В др. случаях существует бесконечно много инвариантных вероятностных мер. Одна из проблем Э. т.- изучение инвариантных мер, принадлежащих какому-либо заранее выбранному классу. Пример такого класса- все инвариантные меры с фиксиров. совокупностью множеств меры 0 (такой же, как у заданной, не обязательно инвариантной меры); другой пример - инвариантные меры, удовлетворяющие вариационному принципу (см. ниже).
Классические эргодические теоремы и проблема эргодичности
Эргодич. теоремы описывают поведение временных средних физ. величин, т. е. ф-ций, определённых на фазовом пространстве (X,
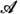 , m) ДС. Для каскада {Т t} временное среднее A t ф-ции f(x), x
, m) ДС. Для каскада {Т t} временное среднее A t ф-ции f(x), x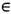 X, на отрезке времени [0, t]определяется равенством
X, на отрезке времени [0, t]определяется равенством

а для потока
Если f -индикатор нек-рого множества F, т. e. f(x) = 1 при х
 F и f( х) = 0 при х
F и f( х) = 0 при х F, то (At f)(x )есть не что иное, как доля времени, проведённого траекторией точки х в множестве F.
F, то (At f)(x )есть не что иное, как доля времени, проведённого траекторией точки х в множестве F.
Первые эргодич. теоремы были доказаны в нач. 30-х гг. Дж. фон Нейманом (J. von Neumann) и Дж. Биркгофом (G. Birkhoff); наз. они соответственно с т а т и с т и ч е с к о й и и н д и в и д у а л ь н о й э р г о д и ч. т е о р е м а м и.
Т е о р е м а ф о н Н е й м а н а утверждает, что если квадрат модуля ф-ции f интегрируем по мере m, то Atf при t
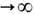 . сходится в среднем квадратическом к нек-рой ф-ции f*, т. е.
. сходится в среднем квадратическом к нек-рой ф-ции f*, т. е.
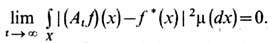
Согласно т е о р е м е Б и р к г о ф а (в формулировке, найденной А. Я. Хинчиным,- отсюда часто употребляемое наименование: т е о р е м а Б и р к г о ф а - Х и н ч и н а), для ф-ции f, модуль к-рой интегрируем, имеет место сходимость (At f)(x)
 f*(x )при всех х вне нек-рого множества нулевой меры (в этом случае говорят: при m-почти всех х, или m-почти всюду). Если временной параметр t принимает как положительные, так и отрицат. значения, то в обеих эргодич. теоремах можно в качестве At брать среднее по отрезку [ - t,0 ] или по симметричному отрезку [- t, t](а также по нек-рым отрезкам, зависящим от t более сложным образом), получая при t
f*(x )при всех х вне нек-рого множества нулевой меры (в этом случае говорят: при m-почти всех х, или m-почти всюду). Если временной параметр t принимает как положительные, так и отрицат. значения, то в обеих эргодич. теоремах можно в качестве At брать среднее по отрезку [ - t,0 ] или по симметричному отрезку [- t, t](а также по нек-рым отрезкам, зависящим от t более сложным образом), получая при t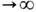 . тот же предел f*.
. тот же предел f*.
Т. о., эргодич. теоремы позволяют говорить о предельных временных средних или о временных средних по бесконечному отрезку времени. Существование последних - признак нек-рой регулярности в поведении траектории ДС, но эта регулярность связана с усреднением, а потому носит лишь статистич. характер. Что касается предельного временного среднего, то его можно охарактеризовать в "геом." терминах, не прибегая к помощи усреднения. Здесь ключевую роль играет понятие и н в а р и а н т н о й ф у н к ц и и. Так называются ф-ции, постоянные вдоль траекторий почти всех точек фазового пространства. Множества, индикаторы к-рых инвариантны, наз. и н в а р и а н тн ы м и м н о ж е с т в а м и. В пространстве L2. инвариантные ф-ции образуют линейное подпространство, и предельное временное среднее f* любой ф-ции f
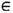 L2 совпадает с её ортогональной проекцией на это подпространство. Аналогичным образом можно охарактеризовать f и в том случае, когда f имеет лишь интегрируемый модуль, т. е. принадлежит пространству L1.
L2 совпадает с её ортогональной проекцией на это подпространство. Аналогичным образом можно охарактеризовать f и в том случае, когда f имеет лишь интегрируемый модуль, т. е. принадлежит пространству L1.
Существуют многочисленные обобщения классич. эргодич. теорем. Одно из них касается ДС с многомерным временным параметром. Если, в частности, t пробегает d- мерное пространство Rd, d>1(система с непрерывным "временем"), или множество целочисленных векторов этого пространства (система с дискретным "временем"), то временное среднее по отрезку заменяется средним по соответствующему d -мерному кубу и эргодич. теоремы фон Неймана и Биркгофа остаются справедливыми.
Особый интерес представляет ситуация, когда не существует никаких инвариантных ф-ций, кроме постоянных (почти всюду), или, что то же самое, когда любое инвариантное множество тривиально в том смысле, что либо оно само, либо его дополнение имеет нулевую меру (такое свойство наз. э р г о д и ч н о с т ь ю). ДС с этим свойством наз. э р г о д и ч е с к о й (иногда также - м е т р и ч е с к и т р а н з и т и в н о й или м е т р и ч е с к и н е р а з л о ж и м о й). В случае эргодич. системы всякое предельное временное среднее представляет собой константу, равную пространственному среднему
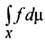 . Т. о., гипотеза Больцмана о равенстве временных и пространственных средних физ. величин сводится к предположению об эргодичности ДС, описывающей движение по гиперповерхности постоянной энергии. Если на фазовом пространстве ДС определена не только мера, но и метрика (т. е. задано расстояние между любыми двумя точками), причём любой шар имеет положительную меру, то из эргодичности следует, что каждая траектория всюду плотна, т. е. проходит произвольно близко от любой точки ("квазиэргодичность"). Обратное, вообще говоря, неверно. Доказательство эргодичности конкретной ДС нередко оказывается весьма трудной задачей, однако общая теория неэргодич. ДС в известном смысле сводится к теории эргодич. систем, т. к. всякая ДС может быть разложена на эргодич. компоненты.
. Т. о., гипотеза Больцмана о равенстве временных и пространственных средних физ. величин сводится к предположению об эргодичности ДС, описывающей движение по гиперповерхности постоянной энергии. Если на фазовом пространстве ДС определена не только мера, но и метрика (т. е. задано расстояние между любыми двумя точками), причём любой шар имеет положительную меру, то из эргодичности следует, что каждая траектория всюду плотна, т. е. проходит произвольно близко от любой точки ("квазиэргодичность"). Обратное, вообще говоря, неверно. Доказательство эргодичности конкретной ДС нередко оказывается весьма трудной задачей, однако общая теория неэргодич. ДС в известном смысле сводится к теории эргодич. систем, т. к. всякая ДС может быть разложена на эргодич. компоненты.
Мультипликативная эргодическая теорема и характеристические показатели
Особое место среди эргодич. теорем занимает м у л ь т и п л и к а т и в н а я э р г о д и ч е с к а я т е о р е м а В. И. О с е л е д е ц а (1968), играющая важную роль в приложениях Э. т. Как и классич. эргодич. теоремы, она описывает поведение ф-ций, заданных на фазовом пространстве ДС, вдоль типичных траекторий. Однако на этот раз речь идёт не о скалярных, а о матричных ф-циях, значения к-рых вдоль траектории не складываются, а перемножаются. Если на фазовом пространстве (X,
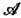 , m) каскада {Т t} задана измеримая ф-ция М со значениями в множестве квадратных матриц k- гoпорядка, то для любого х
, m) каскада {Т t} задана измеримая ф-ция М со значениями в множестве квадратных матриц k- гoпорядка, то для любого х X и любого целого t>=0 естественно рассмотреть произведение Mt(x)= M(x)M(T1x)... M(Ttx). Аналогом индивидуальной эргодич. теоремы служит утверждение, что при условии
X и любого целого t>=0 естественно рассмотреть произведение Mt(x)= M(x)M(T1x)... M(Ttx). Аналогом индивидуальной эргодич. теоремы служит утверждение, что при условии
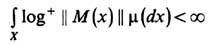
(+ означает, что отрицат. значения log заменяются нулём), запрещающем норме матрицы М(х )при слишком многих х принимать большие значения, для m-почти всех х
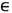 X существует предел
X существует предел

(здесь М' - транспониров. матрица). Структура спектра матрицы L ( х )определяет поведение разл. k -мерных векторов под действием Mt при больших t. Так как L(x) - симметричная и неотрицательно определённая матрица, все её собственные числа неотрицательны, и, взяв из них только попарно различные, можно расположить их в порядке возрастания: 0<l1(x)< ... <lN (х) (N, вообще говоря, зависит от x). Возрастающую цепочку образуют и подпространства Е0( х)... EN(x )пространства R , где Е0( х )состоит из одного нулевого вектора, а Е i (х )при 1<=i<=N натянуто на все собственные векторы матрицы L( х )ссобственными значениями l1( х)...li (х )(очевидно, что EN = Rk). Если вектор и
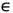 Rk лежит в пространстве Е i при i>=1, но не лежит в Ei-1, то выполняется соотношение
Rk лежит в пространстве Е i при i>=1, но не лежит в Ei-1, то выполняется соотношение
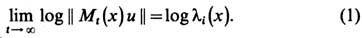
Числа ci(x) = logli(x )наз. х а р а к т е р и с т и ч е с к и м и п о к а з а т е л я м и. Т. <к. EN = Rk, равенство (1) означает, что каждый вектор и
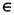 Rk, эволюционирующий под действием М t имеет точный характеристич. показатель, совпадающий с одним из ci(x). Собственные числа li (х )и, следовательно, ci(x )описывают также эволюцию n -мер-ных объёмов Vn (А )множеств А
Rk, эволюционирующий под действием М t имеет точный характеристич. показатель, совпадающий с одним из ci(x). Собственные числа li (х )и, следовательно, ci(x )описывают также эволюцию n -мер-ных объёмов Vn (А )множеств А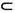 Е п (n=1, ..., N):для любого t>0имеет место равенство
Е п (n=1, ..., N):для любого t>0имеет место равенство
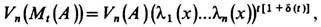
где d(t)
 0 при t
0 при t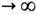 . Поэтому произведение l1(x)... ln (х )можно считать асимптотич. коэф. растяжения n -мерного объёма в пространстве Е n. Как сами li(x), так и их кратности mi(x) - инвариантные ф-ции, поэтому в эргодич. случае все они m-почти всюду постоянны. Для ДС с непрерывным временем имеет место аналогичная картина, только в этом случае исходным объектом является не М(х), а матричнозначная ф-ция двух переменных Mt(x), аналогичная введённому выше семейству произведении и удовлетворяющая тождеству Mt+s(x) = Ms(T tx)Mt(x )(такая ф-ция наз. мультипликативным коциклом над {T t}). Мультипликативную эргодич. теорему часто применяют в ситуации, когда ДС {Tt} определяется системой нелинейных дифференциальных или разностных ур-ний, а матрица Mt(x )отвечает сдвигу на время t вдоль решений линеаризов. системы. В этом случае характеристич. показатели ci(x )(называемые также показателями Ляпунова) непосредственно связаны с характером устойчивости траекторий ( устойчивости движения): если вектор и определяется точкой х и бесконечно близкой к ней точкой х', то положительность ci означает, что под действием Т t точки х и х' при t
. Поэтому произведение l1(x)... ln (х )можно считать асимптотич. коэф. растяжения n -мерного объёма в пространстве Е n. Как сами li(x), так и их кратности mi(x) - инвариантные ф-ции, поэтому в эргодич. случае все они m-почти всюду постоянны. Для ДС с непрерывным временем имеет место аналогичная картина, только в этом случае исходным объектом является не М(х), а матричнозначная ф-ция двух переменных Mt(x), аналогичная введённому выше семейству произведении и удовлетворяющая тождеству Mt+s(x) = Ms(T tx)Mt(x )(такая ф-ция наз. мультипликативным коциклом над {T t}). Мультипликативную эргодич. теорему часто применяют в ситуации, когда ДС {Tt} определяется системой нелинейных дифференциальных или разностных ур-ний, а матрица Mt(x )отвечает сдвигу на время t вдоль решений линеаризов. системы. В этом случае характеристич. показатели ci(x )(называемые также показателями Ляпунова) непосредственно связаны с характером устойчивости траекторий ( устойчивости движения): если вектор и определяется точкой х и бесконечно близкой к ней точкой х', то положительность ci означает, что под действием Т t точки х и х' при t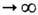 удаляются друг от друга с экспоненциальной скоростью, а отрицательность показателя говорит об их экспоненциальном сближении (о связи показателей Ляпунова с энтропией см. ниже).
удаляются друг от друга с экспоненциальной скоростью, а отрицательность показателя говорит об их экспоненциальном сближении (о связи показателей Ляпунова с энтропией см. ниже).
Э. т. и теория вероятностей
Связь между этими двумя областями можно описать след. образом. Всякий стационарный в узком смысле случайный процесс (см. Стационарный случайный процесс )индуцирует в пространстве своих реализаций [т. е. функций х(s )временного параметра s]. вероятностную меру, инвариантную относительно сдвига S t, определяемого при каждом t соотношением (S tx)(s) = x(s+t). Семейство сдвигов {St} задаёт ДС. Если множество значений процесса конечно или счётно, такая система наз. символической (обычно этот термин употребляется в случае дискретного времени; см. ниже). Возможен и обратный переход от произвольной ДС к стационарному случайному процессу. Действительно, ДС {Т t} сфазовым пространством (X,
 , m) и произвольная измеримая функция f, определённая на X, порождают систему ф-ций {ft}, где ft (х)=f(Т t х), х
, m) и произвольная измеримая функция f, определённая на X, порождают систему ф-ций {ft}, где ft (х)=f(Т t х), х 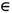 X, к-рая представляет собой стационарный в узком смысле случайный процесс. Семейство сдвигов {St} в пространстве реализаций этого процесса задаёт символич. ДС, называемую ф а к т о р с и с т е м о й ДС { Т t}. Переход к фак-торсистеме можно рассматривать как нек-рое огрубление детальной картины движения, приводящее, вообще говоря, к потере информации. Совокупность факторсистем полностью характеризует систему {Т t}. В эргодич. случае всегда существует такая ф-ция f, принимающая лишь конечное или счётное число значений, что построенная по ней фак-торсистема изоморфна исходной ДС. Следовательно, для этой факторсистемы потери информации не происходит и она одна полностью характеризует систему {Т t}. Раздел теории вероятностей, занимающийся стационарными в узком смысле случайными процессами, является одновременно и частью Э. т. Имеются, однако, нек-рые различия в подходе этих двух теорий к их общему предмету исследования: теория вероятностей в большей степени интересуется свойствами индивидуального процесса, а Э. т.- общими свойствами процессов, получаемых из данной ДС.
X, к-рая представляет собой стационарный в узком смысле случайный процесс. Семейство сдвигов {St} в пространстве реализаций этого процесса задаёт символич. ДС, называемую ф а к т о р с и с т е м о й ДС { Т t}. Переход к фак-торсистеме можно рассматривать как нек-рое огрубление детальной картины движения, приводящее, вообще говоря, к потере информации. Совокупность факторсистем полностью характеризует систему {Т t}. В эргодич. случае всегда существует такая ф-ция f, принимающая лишь конечное или счётное число значений, что построенная по ней фак-торсистема изоморфна исходной ДС. Следовательно, для этой факторсистемы потери информации не происходит и она одна полностью характеризует систему {Т t}. Раздел теории вероятностей, занимающийся стационарными в узком смысле случайными процессами, является одновременно и частью Э. т. Имеются, однако, нек-рые различия в подходе этих двух теорий к их общему предмету исследования: теория вероятностей в большей степени интересуется свойствами индивидуального процесса, а Э. т.- общими свойствами процессов, получаемых из данной ДС.
Стохастичность динамических систем
Статистич. закономерности в поведении ДС проявляются при их наблюдении на больших интервалах времени. Уже одно наличие инвариантной меры m служит причиной нек-рых из этих закономерностей. Так, траектории m-почти всех точек произвольного измеримого множества возвращаются в это множество при как угодно больших значениях t (Пуанкаре теорема). Разные точки могут возвращаться в разные моменты времени, а ср. время до первого возвращения в множество А обратно пропорционально m(A )и, следовательно, очень велико для множеств малой меры. Этот факт придаёт строгость объяснению известного парадокса Э. Цермело, данному Больцманом в кон. 19 в. в ходе возникшей тогда дискуссии о необратимости в статистич. физике.
Другое следствие инвариантности меры-существование для любого измеримого множеств А асимптотич. частоты его посещения типичной траекторией динамич. системы. Эта частота есть временное среднее индикатора множества А, в эргодич. случае она равна m( А).
Эргодичность каскада (или полукаскада) {Т t} равносильна справедливости для любых ф-ций f, g
 L2. соотношения
L2. соотношения
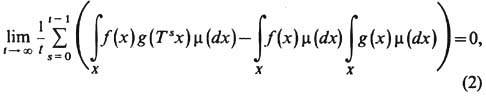
к-рое означает, что предельное временное среднее взаимной ковариационной функции стационарных процессов ft и g t, полученных из ф-ций f и g с помощью ДС, равно нулю (в случае потока эта интерпретация сохраняется). Замена в (2) ковариационной ф-ции её абс. величиной приводит к свойству более сильному, чем эргодичность,- слабому п е р е м е ш и в а н и ю. Ещё более сильное свойство - стремление к нулю при t
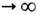 . самой взаимной ковариационной ф-ции, т. е. равенство
. самой взаимной ковариационной ф-ции, т. е. равенство
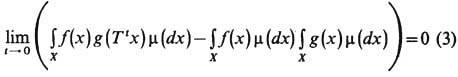
(если t принимает и отрицат. значения, то можно заменить t на - t). ДС со свойством (3) наз. п е р е м е ш и в а ю щ им и (см. также Размешивание). Представив фазовое пространство X в виде ограниченной части плоскости с обычной площадью (мерой Лебега) в роли инвариантной меры m, можно получить следующее наглядное представление об эволюции множеств под действием перемешивающей ДС. Разобьём X на конечное число областей A1, A2, ..., Ak , диаметры к-рых не превосходят нек-рого достаточно малого e>0, и возьмём в качестве g в (3) индикатор произвольного множества В, напр. кружка, изображённого на рис. 3, а в качестве f будем последовательно брать индикаторы множеств А1,..., Ak. Тогда (3) при s=-t>0примет вид
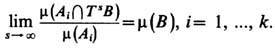
Отсюда видно, что при больших s точки множества T sB занимают почти одну и ту же долю площади каждого А i. Поэтому можно сказать, что множество T sB при s
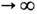 равномерно распределяется по ячейкам А i или что с точностью до s оно равномерно распределяется по пространству X. Конечно, момент времени, начиная с к-рого достигается заданная степень равномерности, может неограниченно расти с уменьшением e. При этом надо учесть, что площадь Т s В не зависит от s и равна площади В. Следовательно, T sB должно иметь весьма причудливую форму, напр. (в простейшем варианте) быть похожим на узкую, длинную и извилистую полоску, с ростом s всё более и более равномерно распределяющуюся по фазовому пространству.
равномерно распределяется по ячейкам А i или что с точностью до s оно равномерно распределяется по пространству X. Конечно, момент времени, начиная с к-рого достигается заданная степень равномерности, может неограниченно расти с уменьшением e. При этом надо учесть, что площадь Т s В не зависит от s и равна площади В. Следовательно, T sB должно иметь весьма причудливую форму, напр. (в простейшем варианте) быть похожим на узкую, длинную и извилистую полоску, с ростом s всё более и более равномерно распределяющуюся по фазовому пространству.
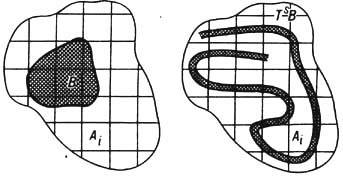
Рис. 3. Под действием перемешивающей системы образ множества В (т. е. T sB )с течением времени всё более равномерно заполняет фазовое пространство.
Для перемешивающих ДС имеет место сходимость к "равновесию" нек-рых "неравновесных" мер, определённых на фазовом пространстве. Речь идёт о мерах v, к-рые можно задать плотностью относительно инвариантной меры m. Преобразование Т t применённое к мере v, превращает её в меру vt, определяемую соотношением vt (А} == v(T-tA),
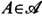 . Если система перемешивает, то vt(A)
. Если система перемешивает, то vt(A) m( А )при t
m( А )при t . для любого
. для любого  , т. е. под действием динамики любая мера из указанного класса сходится к инвариантной мере m.
, т. е. под действием динамики любая мера из указанного класса сходится к инвариантной мере m.
Нек-рые ДС обладают гораздо более сильными свойствами стохастичности, чем перемешивание. Эти свойства можно описать с помощью того же соотношения (3), потребовав на этот раз, чтобы предельный переход был равномерным по тому или иному классу ф-ций. Одно из наиболее сильных свойств указанного типа, называемое К-с в о й с т в о м (в честь А. Н. Колмогорова, к-рый впервые рассмотрел его в кон. 1950-х гг.), допускает неск. эквивалентных формулировок. Одна из них состоит в следующем. Пусть {Т t}- каскад или поток, f(x), х
 X,- ф-ция с конечным числом значений и { ft,
X,- ф-ция с конечным числом значений и { ft, 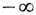 <t<
<t<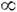 }- порождённый ею стационарный случайный процесс. Для любого s рассмотрим подпространство Н s пространства L2(X,
}- порождённый ею стационарный случайный процесс. Для любого s рассмотрим подпространство Н s пространства L2(X, , m), определяемое поведением этого процесса до момента s. Оно состоит из ф-ций вида j(ft1, ..., ftn, t1, ..., tn<=s, n = 1, 2, ... и их пределов в среднем квадратичном. Очевидно, Hs'
, m), определяемое поведением этого процесса до момента s. Оно состоит из ф-ций вида j(ft1, ..., ftn, t1, ..., tn<=s, n = 1, 2, ... и их пределов в среднем квадратичном. Очевидно, Hs' Hs " при s'<=s ", аф-ции, входящие в Hs при всех s, образуют подпространство
Hs " при s'<=s ", аф-ции, входящие в Hs при всех s, образуют подпространство 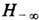 , к-рое естественно связать с поведением процесса в бесконечно далёком прошлом. Процесс ft наз. регулярным, если
, к-рое естественно связать с поведением процесса в бесконечно далёком прошлом. Процесс ft наз. регулярным, если  состоит лишь из констант, т. е. бесконечно далёкое прошлое не несёт информации о процессе. ДС {Т t} наз. К-с и с т е м о й (обладает К-с в о й с т в о м), если любой процесс ft указанного вида регулярен. Аналогичным свойством могут обладать и необратимые ДС (полукаскады и полупотоки). Если полукаскад {T t} обладает этим свойством, то преобразование Т1, порождающее полукаскад, наз. т о ч н ы м э нд о м о р ф и з м о м.
состоит лишь из констант, т. е. бесконечно далёкое прошлое не несёт информации о процессе. ДС {Т t} наз. К-с и с т е м о й (обладает К-с в о й с т в о м), если любой процесс ft указанного вида регулярен. Аналогичным свойством могут обладать и необратимые ДС (полукаскады и полупотоки). Если полукаскад {T t} обладает этим свойством, то преобразование Т1, порождающее полукаскад, наз. т о ч н ы м э нд о м о р ф и з м о м.
Общие свойства К-систем таковы. Все К-системы имеют положит. энтропию и могут даже быть охарактеризованы в энтропийных терминах (см. ниже); К-система с обращённым временем, т. <е. {Т t1}, где Т t1 = Т -t также является К-системой; если каскад {Т n, п =0,b1,...} включён в поток { Т t1, t
 R} в том смысле, что Tn = Т nt01. при нек-ром t0
R} в том смысле, что Tn = Т nt01. при нек-ром t0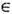 R и любом n, то {Т n} и {Т t1} могут быть К-системами только одновременно; наконец, всякая факторсистема К-системы также является К-системой.
R и любом n, то {Т n} и {Т t1} могут быть К-системами только одновременно; наконец, всякая факторсистема К-системы также является К-системой.
Одно из проявлений стохастичности К-систем - свойство "внутр. случайности". Оно состоит в том, что с помощью нек-рого положит. оператора в L2, обратимого на всюду плотном множестве, можно перевести полугруппу {U t, t>=0} унитарных операторов (обратимых), отвечающих К-системе, в полугруппу необратимых марковских операторов, сходящихся (в нек-ром смысле монотонно) к пределу при t
ДС с наиб. сильными из возможных свойствами стохастичности-это системы Бернулли (Б-системы, названные в честь Я. Бернулли, J. Bernoulli). В случае дискретного времени простейший пример такой системы - семейство сдвигов в пространстве реализаций последовательности независимых одинаково распределённых случайных величин. Термин "Б-с и с т е м а" (а также "Б-с д в и г" и "с д в и г Б е р н у л л и") употребляется по отношению к любой ДС с дискретным временем, изоморфной какой-либо системе описанного вида. Иначе говоря, каскад {Т t} является Б-системой, если на его фазовом пространстве (X,
 , m) можно задать такую ф-цию (случайную величину) f, что случайные величины ft, определённые указанным выше способом, независимы, а наименьшая s-алгебра, относительно к-рой все они измеримы, совпадает с
, m) можно задать такую ф-цию (случайную величину) f, что случайные величины ft, определённые указанным выше способом, независимы, а наименьшая s-алгебра, относительно к-рой все они измеримы, совпадает с  . В случае полукаскада, когда t принимает лишь неотрицат. значения, говорят об одностороннем Б-сдвиге. ДС с непрерывным временем называется Б-системой, если в неё можно включить Б-систему с дискретным временем. Б-системы обладают всеми перечисленными выше свойствами К-систем и подобно К-системам могут быть охарактеризованы внутр. образом с помощью нек-рого условия перемешивания, но с более сильным, чем в случае К-систем, требованием равномерности. Естественным источником Б-систем служит теория вероятностей, но они встречаются также среди ДС геом., алгебраич. и механич. происхождения.
. В случае полукаскада, когда t принимает лишь неотрицат. значения, говорят об одностороннем Б-сдвиге. ДС с непрерывным временем называется Б-системой, если в неё можно включить Б-систему с дискретным временем. Б-системы обладают всеми перечисленными выше свойствами К-систем и подобно К-системам могут быть охарактеризованы внутр. образом с помощью нек-рого условия перемешивания, но с более сильным, чем в случае К-систем, требованием равномерности. Естественным источником Б-систем служит теория вероятностей, но они встречаются также среди ДС геом., алгебраич. и механич. происхождения.
Среди приведённых выше примеров ДС также имеются Б-системы. Это прежде всего преобразование пекаря - оно изоморфно сдвигу Бернулли, отвечающему последовательности независимых случайных величин с равновероятными значениями 0 и 1. Сдвиг Бернулли, у к-рого состояния не равновероятны или их число больше двух, также можно реализовать как отображение квадрата, похожее на преобразование пекаря. Автоморфизм тора порождает Б-систему в том и только том случае, когда у определяющей его матрицы нет собств. чисел, равных по модулю единице. Один из простейших примеров такой матрицы имеет вид
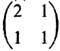
Что касается сдвигов на торе, то они не только не являются Б- или К-системами, но даже не обладают свойством слабого перемешивания, а условие их эргодичности состоит в том, что компоненты вектора a = (1, a1 ..., an) рационально независимы (т. е. линейная комбинация y1a1 + ...+ynan с целыми коэф. y1,..., у n может быть целым числом только в том случае, когда y1=y2=...=yn= 0).
При исследовании стохастичности ДС иногда удаётся обнаружить ф-ции f, к-рые порождают случайные процессы ft с достаточно быстрым, напр. экспоненциально быстрым, убыванием при t
 . ковариационной функции
. ковариационной функции 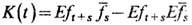 (где Е- матем. ожидание, т. е. интеграл по мере m, а черта означает комплексное сопряжение). Часто оказывается, что те же процессы ft удовлетворяют центральной, предельной теореме[в случае дискрета. времени и веществен, ф-ции f последнее означает, что распределение случайной величины (DSn)-1/2(Sn - ESn), где Sn=f0+...+fn-1, а DSn = E(Sn - ESn)2 - дисперсия, стремится при t
(где Е- матем. ожидание, т. е. интеграл по мере m, а черта означает комплексное сопряжение). Часто оказывается, что те же процессы ft удовлетворяют центральной, предельной теореме[в случае дискрета. времени и веществен, ф-ции f последнее означает, что распределение случайной величины (DSn)-1/2(Sn - ESn), где Sn=f0+...+fn-1, а DSn = E(Sn - ESn)2 - дисперсия, стремится при t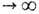 к нормальному распределению с нулевым матем. ожиданием и единичной дисперсией]. Ф-ции f с этими свойствами могут существовать даже в том случае, когда система обладает не очень явно выраженной стоха-стичностью, но наличие таких свойств у самых простых и естеств. ф-ций, определённых на фазовом пространстве,- достаточно надёжный признак стохастичности.
к нормальному распределению с нулевым матем. ожиданием и единичной дисперсией]. Ф-ции f с этими свойствами могут существовать даже в том случае, когда система обладает не очень явно выраженной стоха-стичностью, но наличие таких свойств у самых простых и естеств. ф-ций, определённых на фазовом пространстве,- достаточно надёжный признак стохастичности.
Спектр динамической системы
Многие свойства ДС могут быть описаны на языке спектральной теории операторов (см. Спектр оператора). Операторы Ut, отвечающие каскаду или потоку {Т t}, образуют однопараметрич. группу линейных унитарных операторов в гильбертовом пространстве L2. Эти операторы всегда обладают собств. значением l=1 (с собств. ф-циями f=const), составляющим тривиальную часть спектра. По этой причине, говоря о спектре ДС {Т t}, обычно имеют в виду спектр полугруппы {Ut} в инвариантном подпространстве L02, ортогональном к одномерному подпространству констант, причём под спектром понимается не просто набор собственных и квазисобственных чисел, а вся совокупность унитарных инвариантов, т. е. таких характеристик группы операторов, к-рые определяют её однозначно с точностью до унитарной эквивалентности. Общая структура спектра, одинаковая для всех однопараметрич. групп унитарных операторов в L02, определяется совокупностью спектральных мер sf,f
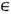 L02. Мера sf находится из соотношения
L02. Мера sf находится из соотношения
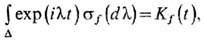
где D=[ - p, p) в случае каскада, D= (
 ) в случае потока и
) в случае потока и
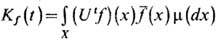
-ковариационная ф-ция процесса ft= Utf. В обоих случаях все меры sf (определённые на D) конечны. Среди них всегда есть такая sf0 =
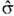 , относительно к-рой всякая другая sf задаётся плотностью: sf(dl) =pf(l)
, относительно к-рой всякая другая sf задаётся плотностью: sf(dl) =pf(l)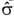 (dl)(тогда говорят, что sf а б с о л ю т н о н е п р е р ы в н а о т н о с и т е л ьн о
(dl)(тогда говорят, что sf а б с о л ю т н о н е п р е р ы в н а о т н о с и т е л ьн о 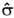 , и пишут
, и пишут  ; если, кроме того,
; если, кроме того, 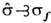 , то sf и
, то sf и 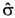 наз. э к в и в а л е н т н ы м и). Она наз. мерой м а к с им а л ь н о г о с п е к т р а л ь н о г о т и п а. Если подпространство H(f)
наз. э к в и в а л е н т н ы м и). Она наз. мерой м а к с им а л ь н о г о с п е к т р а л ь н о г о т и п а. Если подпространство H(f)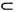 L20, порождённое всеми Utf, совпадает с L20, то говорят, что {Ut} имеет п р о с т о й с п е к т р. Если существует такая конечная или бесконечная последовательность f1, f2,..., что меры mfi абсолютно непрерывны относительно друг друга, подпространства H(fi )попарно ортогональны, а их сумма есть всё L20, то спектр называется о д н о р о дн ы м. Число элементов последовательности f1, f2, ... наз. к р а т н о с т ь ю с п е к т р а. Если при этом все sfi эквивалентны мере Лебега, то спектр наз. л е б е г о в с к и м.
L20, порождённое всеми Utf, совпадает с L20, то говорят, что {Ut} имеет п р о с т о й с п е к т р. Если существует такая конечная или бесконечная последовательность f1, f2,..., что меры mfi абсолютно непрерывны относительно друг друга, подпространства H(fi )попарно ортогональны, а их сумма есть всё L20, то спектр называется о д н о р о дн ы м. Число элементов последовательности f1, f2, ... наз. к р а т н о с т ь ю с п е к т р а. Если при этом все sfi эквивалентны мере Лебега, то спектр наз. л е б е г о в с к и м.
Обладая свойствами, общими для всех групп унитарных операторов, спектр ДС имеет и нек-рую специфику, связанную с тем, что операторы Ut не только линейны, но и мультипликативны: U tfg=U tfU tg. В частности, собств. значения каждого из них образуют подгруппу группы комплексных чисел, равных по модулю единице.
Однако полное описание всех видов спектра, к-рый может встретиться у ДС, до сих пор отсутствует. Неизвестно, напр., может ли спектр быть конечнократным лебеговским.
Свойства ДС, к-рые можно выразить в терминах спектра, наз. спектральными и служат предметом спектрального направления Э. <т. Так, эргодичность каскада {Т t} равносильна отсутствию у оператора U1 к.-л. собственных ф-ций с собственным значением "единица", кроме постоянных; все другие собственные подпространства этого оператора в эргодич. случае также одномерны и состоят из постоянных по модулю ф-ций. Слабое перемешивание - это отсутствие собств. значений, отличных от единицы: в этом случае говорят, что система имеет непрерывный спектр. Перемешивание также является спектральным свойством. Однако для К-свойства это уже неверно. Все К-системы имеют один и тот же - счётнократный лебегов-ский спектр, но известны ДС с таким же спектром, не являющиеся К-системами. Для систем с дискретным спектром (когда собств. ф-ции образуют базис в L2) ситуация обратная: всякая такая система однозначно (с точностью до изоморфизма) определяется своим спектром (фон Нейман, 1932). Пример системы с дискретным спектром - семейство сдвигов на торе.
В исследованиях (прежде всего численных) конкретных ДС большую роль играет вычисление корреляционных ф-ций Kf(t )и отвечающих им спектральных мер sf. В то же время полное аналитич. исследование спектра во мн. случаях является трудной задачей.
Энтропийная теория динамических систем
Это направление Э. <т. возникло в кон. 50-х - нач. 60-х гг. после того, как А. Н. Колмогоровым было введено понятие энтропии ДС, близкое к теоретико-информац. энтропии К. Э. Шеннона (С. Е. Shannon) (см. Теория информации). Пусть измеримые множества A1,...,Ak образуют разбиение а вероятностного пространства (X,
 , m). Энтропией этого разбиения наз. число
, m). Энтропией этого разбиения наз. число
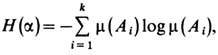
полагая здесь 0log0 = 0 (основание логарифмов существенной роли не играет, но во многих случаях логарифмы удобно считать натуральными). Очевидно, H(a) не зависит от того, в каком порядке занумерованы множества А i. Если Т- сохраняющее меру преобразование, то при любом m>0 множества Т -m А i ,1<=i<=k, также образуют разбиение (обозначаемое T-ma). Доказывается, что всегда существует конечный предел
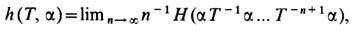
где aT1 a... Т -n+1a- разбиение, образованное всеми множествами вида
 (нек-рые из них могут оказаться пустыми). По определению, энтропия h(Т )преобразования Т, часто называемая э н т р о п ие й К о л м о г о р о в а - С и н а я, есть sup h(T, a) по всем конечным разбиениям a. Т. <к. каскад (или полукаскад) {Т t} полностью определяется преобразованием Т1, его энтропию отождествляют с h(T1). Энтропия потока (или полупотока) также отождествляется с h(T1), что оправдывается тождеством h(Tt) = |t|h(T1 )(справедливым и для дискретного времени).
(нек-рые из них могут оказаться пустыми). По определению, энтропия h(Т )преобразования Т, часто называемая э н т р о п ие й К о л м о г о р о в а - С и н а я, есть sup h(T, a) по всем конечным разбиениям a. Т. <к. каскад (или полукаскад) {Т t} полностью определяется преобразованием Т1, его энтропию отождествляют с h(T1). Энтропия потока (или полупотока) также отождествляется с h(T1), что оправдывается тождеством h(Tt) = |t|h(T1 )(справедливым и для дискретного времени).
Энтропия ДС может принимать любые неотрицат. значения, включая значение
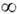 . Изоморфные ДС имеют одинаковую энтропию.
. Изоморфные ДС имеют одинаковую энтропию.
Наглядное представление о смысле понятия энтропии (допускающее для нек-рых классов ДС строгое обоснование) можно получить следующим образом. Пусть {Т t} - эргодич. каскад, фазовым пространством к-poгo служит двумерная область, а инвариантной мерой m - площадь (мера Лебега). Применив преобразование Т t к кружку В малого радиуса s, получим множество Т t В той же площади, но, возможно, др. формы. Если энтропия положительна, то граница области Т t В с ростом t будет становиться всё более извилистой, нерегулярной. Величину этой нерегулярности можно измерить площадью e-окрестности множества Т t В: при не очень больших t (порядка |ln e| она увеличится по сравнению с площадью В примерно в ехр(ht) раз, где h - энтропия каскада. При h = 0 эта площадь растёт медленнее, чем экспоненциально, или не растёт совсем. В неэргодич. случае фазовое пространство разбивается на инвариантные части А1 ..., А n, в каждой из к-рых может быть свой показатель скорости, а энтропия получается усреднением этих показателей с весами m(Ai), i= 1,... ,п. Отсюда видно, что энтропия характеризует скорость искажения границ малых областей правильной формы, а положительность энтропии означает, что в какой-то части фазового пространства эта скорость экспоненциальна. Родственное свойство ДС - перемешивание. Но оно, во-первых, касается всего фазового пространства, во-вторых, может иметь любую скорость. Т. о., эти два свойства до нек-рой степени независимы. Тем не менее известно, что у всякой системы с положит. энтропией найдётся перемешивающая факторсистема (см. ниже).
Осн. задачи, решаемые энтропийной теорией,- вычисление (оценка) энтропии для тех или иных классов систем и выяснение взаимоотношений между энтропией и др. характеристиками ДС. Для сдвига в пространстве реализаций последовательности независимых, одинаково распределённых случайных величин xn (Б-сдвига) энтропия равна H(x1). В классе Б-каскадов и Б-потоков энтропия играет определяющую роль, являясь полным инвариантом: две такие ДС изоморфны, если они имеют одинаковую энтропию (т е о р е м а О р н с т е й н а; D. Ornstein, 1970). Для класса К-систем (включающего Б-системы в качестве подкласса) это уже не так: существует несчётное семейство попарно неизоморфных К-систем с одинаковой энтропией (правда, все известные К-системы физ. происхождения являются Б-системами). Но и с К-системами энтропия связана самым непосредств. образом, т. к. К-системы и только они имеют вполне п о л о ж и т. э н т р о п и ю: любая нетривиальная факторсистема такой системы имеет положит. энтропию (т е о р е м а Р о х л и н а - С и н а я; В. А. Рохлин, Я. Г. Синай, 1961). Тем самым у К-свойства имеется чисто энтропийный эквивалент.
К-системы входят в класс ДС с положит. энтропией. В нём уже встречаются системы, к-рые не перемешивают, и даже неэргодич. системы. Однако у любой эргодич. системы из этого класса, имеющей энтропию h >0, найдётся факторсистема с любой наперёд заданной энтропией h1<=h, к-рая является Б-системой (т е о р е м а С и н а я, 1962).
С точки зрения энтропийной теории противоположными К-системам свойствами обладают системы с нулевой энтропией, для них энтропийная теория гораздо менее содержательна, чем для систем с положит. энтропией. В то же время систем с нулевой энтропией достаточно много (в нек-ром точно формулируемом смысле они составляют подавляющее большинство среди всех ДС). К этому классу относятся все системы с дискретным спектром, но в нём встречаются перемешивающие системы и даже системы с таким же, как у К-систем, счётнократным лебеговским спектром.
Для гладких ДС известна связь между энтропией h и характеристич. показателями ci ( х):
где т i (х)- кратность показателя ci( х) и k(x)- число положит. показателей (показатели считаются занумерованными в порядке убывания). Для нек-рых инвариантных мер m здесь достигается равенство, к-рое показывает, что энтропия характеризует степень неустойчивости траектории ДС. Оно служит важным инструментом оценки энтропии при численном исследовании ДС.
Кроме энтропии в Э. т. существует ещё одно понятие, близкое к ней по смыслу, но непосредственно не связанное с инвариантной мерой. Речь идёт о т о п о л о г и ч. э н т р оп и и- числовой характеристике топологич. ДС. Такая система представляет собой группу или полугруппу непрерывных преобразований метрич. пространства X. Задав на X вероятностную меру m, инвариантную относительно рассматриваемого семейства преобразований, получим ДС в смысле Э. т. Эта система имеет энтропию hm, зависящую, вообще говоря, от m. Если фазовое пространство X компактно, то sup hm по всем инвариантным мерам совпадает с топологич. энтропией htop. Отсюда следует, что htop является инвариантом непрерывного изоморфизма топологич. ДС: если между фазовыми пространствами двух таких систем имеется взаимно однозначное соответствие, при к-ром каждому борелевскому множеству в одном из них отвечает борелевское множество в другом, а преобразования, образующие ДС, переходят друг в друга, то эти системы имеют одинаковую топологич. энтропию. Мера m, для к-рой hm = htop, наз. мерой с макс. энтропией. Такова, напр., мера Лебега для автоморфизма тора. Но меры с макс. энтропией может и не быть. Задача об условиях существования и свойствах таких мер служит одним из звеньев, связывающих Э. т. со статистич. физикой. Под влиянием последней в Э. т. в 70-х гг. появилось обобщение топологич. энтропии, называемое топологич. давлением (см. ниже).
Символическая динамика
С и м в о л и ч е с к о й ДС наз. каскад {Sn}, образованный сдвигами в пространстве последовательностей. В простейшем случае фазовым пространством такой системы служит множество
 всех последовательностей y={ у i,
всех последовательностей y={ у i,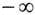 <i<
<i<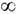 }, элементы к-рых принадлежат нек-ро-му конечному или счётному множеству А("алфавиту"), а преобразование S = S1 (сдвиг влево) переводит у в последовательность у' = {у'i, -
}, элементы к-рых принадлежат нек-ро-му конечному или счётному множеству А("алфавиту"), а преобразование S = S1 (сдвиг влево) переводит у в последовательность у' = {у'i, - <i<
<i<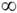 }, где y'i=yi+1. В общем случае фазовым пространством символич. системы может быть не всё пространство последовательностей
}, где y'i=yi+1. В общем случае фазовым пространством символич. системы может быть не всё пространство последовательностей  , а любое его подмножество Y, инвариантное относительно сдвига. Оно может иметь очень сложную структуру, но особенно важную роль играют относительно простые множества Y, наз. м а р к о в с к и м и. Такое множество состоит из всех последовательностей, не содержащих ни одной пары стоящих рядом символов из заданного набора таких пар (напр., Y может состоять из всех последовательностей нулей и единиц, в к-рых две единицы нигде не стоят рядом). Семейство сдвигов {Sn}, определённое на марковском множестве, наз. с и м в о л и ч е с к о й (чаще т о п о л ог и ч е с к о й) ц е п ь ю М а р к о в а. Как правило, символич. система обладает бесконечным набором инвариантных вероятностных мер, но бывают множества Y (в т. ч. нетривиальные), для к-рых такая мера единственна. Всякая инвариантная вероятностная мера превращает последовательность координат yi, рассматриваемых как ф-ции от у, в стационарную случайную последовательность со значениями в А.
, а любое его подмножество Y, инвариантное относительно сдвига. Оно может иметь очень сложную структуру, но особенно важную роль играют относительно простые множества Y, наз. м а р к о в с к и м и. Такое множество состоит из всех последовательностей, не содержащих ни одной пары стоящих рядом символов из заданного набора таких пар (напр., Y может состоять из всех последовательностей нулей и единиц, в к-рых две единицы нигде не стоят рядом). Семейство сдвигов {Sn}, определённое на марковском множестве, наз. с и м в о л и ч е с к о й (чаще т о п о л ог и ч е с к о й) ц е п ь ю М а р к о в а. Как правило, символич. система обладает бесконечным набором инвариантных вероятностных мер, но бывают множества Y (в т. ч. нетривиальные), для к-рых такая мера единственна. Всякая инвариантная вероятностная мера превращает последовательность координат yi, рассматриваемых как ф-ции от у, в стационарную случайную последовательность со значениями в А.
Символич. системы играют в Э. т. двоякую роль. Во-первых, они используются для проверки тех или иных общих идей, во-вторых, составляют основу метода символич. динамики, позволяющего успешно изучать нек-рые классы ДС путём построения их символич. моделей. Суть этого метода, восходящего к Ж. Адамару (J. S. Hadamard), Биркгофу и М. Морсу (М. С. Morse), состоит в следующем. Пусть {Т n} - каскад с фазовым пространством X и f- ф-ция на X со значениями в конечном или счётном множестве А. Тогда каждой точке х
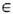 X можно поставить в соответствие последовательность y(x) ={f(Tnx), -
X можно поставить в соответствие последовательность y(x) ={f(Tnx), - <п<
<п<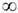 } элементов множества А. Очевидно, точке Т1 х отвечает последовательность Sly, где S1- сдвиг на один символ влево, а множество Yf всех полученных т. <о. последовательностей инвариантно относительно S1. Возникает символич. ДС, связанная с ф-цией f, точнее, с разбиением af пространства X на множества, где f принимает фиксиров. значения (изменение самих этих значений приводит к простой замене символов). Если m - инвариантная мера системы {Т n}, то отображение, переводящее х в у(х), индуцирует на Yf меру mf по ф-ле mf (В} =m({х
} элементов множества А. Очевидно, точке Т1 х отвечает последовательность Sly, где S1- сдвиг на один символ влево, а множество Yf всех полученных т. <о. последовательностей инвариантно относительно S1. Возникает символич. ДС, связанная с ф-цией f, точнее, с разбиением af пространства X на множества, где f принимает фиксиров. значения (изменение самих этих значений приводит к простой замене символов). Если m - инвариантная мера системы {Т n}, то отображение, переводящее х в у(х), индуцирует на Yf меру mf по ф-ле mf (В} =m({х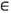 Х:у (х)
Х:у (х) В}), к-рая инвариантна относительно {Sn}. Иногда удаётся подобрать f так, что с точностью до множества нулевой меры каждому у
В}), к-рая инвариантна относительно {Sn}. Иногда удаётся подобрать f так, что с точностью до множества нулевой меры каждому у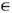 Yf отвечает только одно х, т. е. m-почти всякая точка х однозначно определяется тем, какие элементы разбиения af она последовательно посещает под действием преобразований Т n. Тогда системы {Т n} и {Sn} oказываются изоморфными, а af наз. о б р а з у ю щ и м р а з б и е н и е м или просто о б р а з у ющ е й для {Т n}. Всякий эргодич. каскад обладает счётной образующей, а при условии конечности его энтропии даже конечной.
Yf отвечает только одно х, т. е. m-почти всякая точка х однозначно определяется тем, какие элементы разбиения af она последовательно посещает под действием преобразований Т n. Тогда системы {Т n} и {Sn} oказываются изоморфными, а af наз. о б р а з у ю щ и м р а з б и е н и е м или просто о б р а з у ющ е й для {Т n}. Всякий эргодич. каскад обладает счётной образующей, а при условии конечности его энтропии даже конечной.
Гиперболические системы
Понятие гиперболичности служит матем. выражением и конкретизацией свойства локальной неустойчивости траекторий. Обычно предполагается, что фазовым пространством системы служит нек-рое риманово многообразие (см. Риманово пространство) X, а динамика задаётся гладким отображением Т1 = Т: X
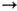 X (случай каскада) или гладким векторным полем на X (случай потока). Наличие римановой структуры позволяет измерять длины кривых и объёмы подмножеств, принадлежащих X, а также длины векторов в касательных пространствах к X. Гиперболичность - это свойство отд. траекторий О(х) = {Т t х}, формулируемое в терминах касательных отображений (решений ур-ний в вариациях - в случае потока), отвечающих ДС {Т t}. Его смысл в том, что при каждом t имеется три типа поведения точек, бесконечно близких к точке Т t х: при своём дальнейшем движении под действием ДС точки первого типа с экспоненциальной скоростью сближаются с траекторией точки х, точки второго типа с экспоненциальной скоростью удаляются от неё, а точки третьего (нейтрального) типа ведут себя промежуточным образом. Этим трём типам поведения отвечает представление касательного пространства к X в точке Т t х в виде прямой суммы подпространств, переходящих друг в друга вдоль траектории под действием касательных отображений. В случае каскада точек нейтрального типа может не быть совсем, а в случае потока они всегда есть - из таких точек состоит сама траектория О(х). При изменении направления времени точки первого и второго типа меняются ролями, а точки третьего типа сохраняются.
X (случай каскада) или гладким векторным полем на X (случай потока). Наличие римановой структуры позволяет измерять длины кривых и объёмы подмножеств, принадлежащих X, а также длины векторов в касательных пространствах к X. Гиперболичность - это свойство отд. траекторий О(х) = {Т t х}, формулируемое в терминах касательных отображений (решений ур-ний в вариациях - в случае потока), отвечающих ДС {Т t}. Его смысл в том, что при каждом t имеется три типа поведения точек, бесконечно близких к точке Т t х: при своём дальнейшем движении под действием ДС точки первого типа с экспоненциальной скоростью сближаются с траекторией точки х, точки второго типа с экспоненциальной скоростью удаляются от неё, а точки третьего (нейтрального) типа ведут себя промежуточным образом. Этим трём типам поведения отвечает представление касательного пространства к X в точке Т t х в виде прямой суммы подпространств, переходящих друг в друга вдоль траектории под действием касательных отображений. В случае каскада точек нейтрального типа может не быть совсем, а в случае потока они всегда есть - из таких точек состоит сама траектория О(х). При изменении направления времени точки первого и второго типа меняются ролями, а точки третьего типа сохраняются.
Важнейшим инструментом исследования ДС гипербо-лич. типа служат устойчивые и неустойчивые многообразия. Устойчивое многообразие W s(x )точки х состоит из всех точек у, для к-рых расстояние между Т t х и Т t у стремится к нулю при t
 , а неустойчивое многообразие Wu (х )образовано точками у, к-рые ведут себя точно так же, но при t
, а неустойчивое многообразие Wu (х )образовано точками у, к-рые ведут себя точно так же, но при t -
- . Под действием Т t устойчивые многообразия переходят друг в друга: T tW s(x)=W s(T tx), то же самое относится к неустойчивым многообразиям.
. Под действием Т t устойчивые многообразия переходят друг в друга: T tW s(x)=W s(T tx), то же самое относится к неустойчивым многообразиям.
Наиб. полно свойство гиперболичности проявляется у с и с т е м А н о с о в а, введённых Д. В. Аносовым в нач. 60-х гг. (первоначальное назв.- У-системы). У таких систем в случае дискретного времени отсутствуют точки нейтрального типа, а в случае непрерывного времени множество точек нейтрального типа для х исчерпывается траекторией О(х). Кроме того, для систем Аносова константы, характеризующие экспоненциальное сближение траекторий, можно выбрать едиными для всех точек фазового пространства.
Простейший пример системы Аносова - автоморфизм двумерного тора, отвечающий матрице
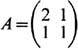 . Собств. числа этой матрицы равны соответственно l1 = (3-
. Собств. числа этой матрицы равны соответственно l1 = (3- )/2< 1 и l2 = 1/l1 а собств. направления определяются взаимно перпендикулярными векторами е1=(2,
)/2< 1 и l2 = 1/l1 а собств. направления определяются взаимно перпендикулярными векторами е1=(2, 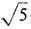 -1) и е2=(2,-
-1) и е2=(2,- -1). Устойчивое и неустойчивое многообразия произвольной точки х - это траектории обмотки, проходящие через х в направлении соответственно е1. и е2 (рис. 4). Каждая из этих кривых всюду плотна на торе, что типично для систем Аносова, а их взаимная перпендикулярность-случайное обстоятельство, связанное с симметричностью матрицы А. В случае матрицы А произвольного порядка п (с целочисленными элементами и определителем +1) соответствующий автоморфизм n -мерного тора является системой Аносова в том и только том случае, когда у неё нет собственных чисел, лежащих на единичной окружности.
-1). Устойчивое и неустойчивое многообразия произвольной точки х - это траектории обмотки, проходящие через х в направлении соответственно е1. и е2 (рис. 4). Каждая из этих кривых всюду плотна на торе, что типично для систем Аносова, а их взаимная перпендикулярность-случайное обстоятельство, связанное с симметричностью матрицы А. В случае матрицы А произвольного порядка п (с целочисленными элементами и определителем +1) соответствующий автоморфизм n -мерного тора является системой Аносова в том и только том случае, когда у неё нет собственных чисел, лежащих на единичной окружности.
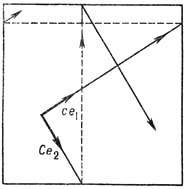
Рис. 4. Векторы, пропорциональные е1 и е2, и отрезки проходящих черезних траекторий обмотки.
Самый известный пример системы Аносова с непрерывным временем - геодезич. поток на компактной поверхности М постоянной отрицат. кривизны. Фазовое пространство этой ДС образовано всеми касательными к М векторами длины 1, каждый из к-рых движется с единичной скоростью вдоль определяемой им геодезической линии. К геодезич. потоку приводится гамильтонова система с гамильтонианом Н= Т+ V, если Т квадратично зависит от импульсов, а V зависит только от координат. Соответствующая риманова метрика определяется гамильтонианом, но отрицательная кривизна появляется лишь при Н спец. вида.
Системы Аносова демонстрируют простейший, идеальный тип гиперболич. поведения и редко встречаются в приложениях. Гораздо чаще условия гиперболичности выполняются лишь для траекторий, заполняющих нек-рое инвариантное множество, не совпадающее со всем фазовым пространством. При этом, в зависимости от того, существуют ли точки нейтрального типа и равномерна ли экспоненциальная скорость сближения траекторий в определении гиперболичности, различают полную и частичную, а также равномерную и неравномерную гиперболичности (здесь возможны любые комбинации). Полная и частичная гиперболичности выражаются в терминах характеристич. показателей: грубо говоря, первое свойство - это отсутствие нулевых, а второе - наличие ненулевых показателей.
Как правило, гиперболич. множество имеет нулевой ри-манов объём и вследствие этого нигде не плотно, т. е. не содержит ни одного шара (в двумерном случае - круга). Тривиальный пример такого множества - гиперболич. неподвижная точка х (седло) нек-рого гладкого преобразования плоскости. В её окрестности, однако, может существовать гиперболич. множество гораздо более сложной структуры (оно замкнуто, нигде не плотно и не содержит изолиров. точек, т. е. напоминает канторово совершенное множество). Это бывает в тех случаях, когда проходящие через точку х сепаратрисы (к-рые служат для неё устойчивым и неустойчивым многообразиями) пересекаются под ненулевым углом (трансверсально) в нек-рой точке у
 х (называемой трансверсальной гомоклинич. точкой).
х (называемой трансверсальной гомоклинич. точкой).
Если гиперболич. множество Г одновременно является аттрактором, т. е. притягивает при t
 . все траектории из нек-рой своей окрестности, то оно должно содержать неустойчивое многообразие каждой своей точки. Т. о., в двумерном случае гиперболич. аттрактор локально представляет собой семейство более или менее параллельных друг другу кривых, проведённых через каждую точку нек-рого множества канторовского типа, лежащего на прямой, перпендикулярной направлению кривых. Аттракторы такого типа получили наименование странных аттракторов. Аналогичную структуру имеют гиперболич. аттракторы в многомерном случае. Один из наиб. известных примеров гиперболич. аттрактора - аттрактор Лоренца (см. Лоренца система).
. все траектории из нек-рой своей окрестности, то оно должно содержать неустойчивое многообразие каждой своей точки. Т. о., в двумерном случае гиперболич. аттрактор локально представляет собой семейство более или менее параллельных друг другу кривых, проведённых через каждую точку нек-рого множества канторовского типа, лежащего на прямой, перпендикулярной направлению кривых. Аттракторы такого типа получили наименование странных аттракторов. Аналогичную структуру имеют гиперболич. аттракторы в многомерном случае. Один из наиб. известных примеров гиперболич. аттрактора - аттрактор Лоренца (см. Лоренца система).
Естеств. кандидат на роль инвариантной меры гиперболич. системы - это риманов объём (соответствующим образом нормированный). Однако он инвариантен лишь в нек-рых, весьма спец. ситуациях (напр., для автоморфизмов тора). Если же риманов объём р не инвариантен, а ДС представляет собой каскад Аносова, то она диссипативна относительно r: существует множество, образы к-рого под действием Т t при разных t попарно не пересекаются и покрывают всё фазовое пространство. Тем не менее из r можно получить инвариантную меру. Для этого нужно, начав с любой абсолютно непрерывной вероятностной меры m (т. <е. меры задаваемой плотностью относительно r), ввести последовательность мер mn, где
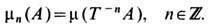
В случае системы Аносова, обладающей хотя бы одной всюду плотной траекторией (это свойство наз. топологической транзитивностью), последовательность mn слабо сходится при п
 +
+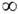 и п
и п -
- . к инвариантным мерам m+ и m- соответственно (слабая сходимость mn
. к инвариантным мерам m+ и m- соответственно (слабая сходимость mn v означает, что
v означает, что 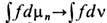 для любой ограниченной непрерывной ф-ции f). Меры m+ и m- не зависят от m и, как правило, различны.
для любой ограниченной непрерывной ф-ции f). Меры m+ и m- не зависят от m и, как правило, различны.
В более общем случае, когда система обладает гиперболич. аттрактором Г, а m - вероятностная мера, сосредоточенная в его окрестности и имеющая плотность относительно r, последовательность mn при п
 . слабо сходится к инвариантной мере, сосредоточенной на Г. При нек-рых более общих условиях к инвариантной мере сходятся лишь средние арифметические
. слабо сходится к инвариантной мере, сосредоточенной на Г. При нек-рых более общих условиях к инвариантной мере сходятся лишь средние арифметические 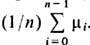
Роль устойчивых и неустойчивых многообразий в изучении эргодич. свойств гиперболич. систем иллюстрирует следующее рассуждение Э. Хопфа (Е. Hopf). Если две точки лежат на одном устойчивом многообразии, то при t-> оо они сближаются, а потому для любой непрерывной ф-ции f её временное среднее f* принимает одинаковые значения в тех точках этого многообразия, где ф-ция f* определена. То же самое верно при t
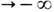 . для точек любого неустойчивого многообразия, а т. к. по теореме Биркгофа f* существует на множестве полной меры, найдётся такая ф-ция
. для точек любого неустойчивого многообразия, а т. к. по теореме Биркгофа f* существует на множестве полной меры, найдётся такая ф-ция  постоянная на каждом W s(x} и на каждом Wu(x), что
постоянная на каждом W s(x} и на каждом Wu(x), что 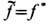 всюду, кроме, быть может, множества нулевой меры. Очевидно,
всюду, кроме, быть может, множества нулевой меры. Очевидно,  = const, если выполняется следующее условие связности: для любых точек х, х' можно подобрать цепочку точек у0, y1,...,у n, в к-рой у0=х, у n = х', и при любом k<n точки yk и yk+1 принадлежат либо одному устойчивому, либо одному неустойчивому многообразию. Пользуясь тем, что всякая интегрируемая ф-ция приближается непрерывными ф-циями, можно распространить утверждение о постоянстве (почти всюду) средних f* на все интегрируемые ф-ции f и тем самым доказать эргодичность.
= const, если выполняется следующее условие связности: для любых точек х, х' можно подобрать цепочку точек у0, y1,...,у n, в к-рой у0=х, у n = х', и при любом k<n точки yk и yk+1 принадлежат либо одному устойчивому, либо одному неустойчивому многообразию. Пользуясь тем, что всякая интегрируемая ф-ция приближается непрерывными ф-циями, можно распространить утверждение о постоянстве (почти всюду) средних f* на все интегрируемые ф-ции f и тем самым доказать эргодичность.
В целом гиперболич. системы можно считать, хотя и с нек-рыми оговорками, в высокой степени стохастич-ными. Так, известно, что если каскад {Т t} обладает гиперболич. множеством Г с достаточно естеств. свойствами, то для широкого класса инвариантных мер, сосредоточенных на Г, он эргодичен, но может иметь в спектре дискретную компоненту, препятствующую перемешиванию. В последнем случае Г можно разбить на части Г 0, Г 1 ,..., Г k-1, циклически переставляемые отображением Т1, причём подкаскад {T kt} является Б-системой на множестве Г 0, к-рое, очевидно, {T kt}-инвариантно. Кроме того, для большинства случайных последовательностей ft, порождённых достаточно гладкими ф-циями f по ф-ле ft(x)=f(T tx), выполняется центральная предельная теорема. Всё сказанное касается, в частности, систем Аносова: если к тому же для такой системы риманов объём инвариантен, то дискретная компонента в её спектре отсутствует и она является Б-системой.
Методы, развитые в теории гиперболич. систем, нашли приложение в теории систем биллиардного типа и в теории одномерных отображений.
Динамические системы биллиардного типа
ДС (поток), описывающая точечную частицу, к-рая движется по инерции внутри нек-рой области Q , отражаясь от её границы дQ по закону "угол падения равен углу отражения", наз. б и л л и а р д н о й с и с т е м о й или м а т е м а т и ч. б и л л и а р д о м. Т. к. длина вектора скорости при таком движении не зависит от времени, в качестве фазового пространства X берётся совокупность всех векторов постоянной (напр., единичной) длины, приложенных в точках множества
 . Если Q - область n -мерного пространства Rn, то X можно отождествить с множеством пар (q,u), где
. Если Q - область n -мерного пространства Rn, то X можно отождествить с множеством пар (q,u), где 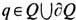 , а u - точка n-1-мерной сферы Sn-1 , т. е.
, а u - точка n-1-мерной сферы Sn-1 , т. е. 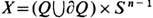 . Инвариантная мера имеет вид dqdu, где dq- элемент n -мерного объёма, a du- элемент п-1-мерного объёма на Sn-1.
. Инвариантная мера имеет вид dqdu, где dq- элемент n -мерного объёма, a du- элемент п-1-мерного объёма на Sn-1.
С биллиардами связаны нек-рые задачи классич. и квантовой механики. Так, движение по отрезку прямой п материальных точек, упруго сталкивающихся друг с другом и с концами отрезка, сводится к биллиарду в n -мерном многограннике (при п=2- втреугольнике). Аналогичная система из п упругих шаров в прямоугольном ящике сводится к биллиарду в более сложной области, граница к-рой состоит из кусков цилиндрич. гиперповерхностей. В этих примерах постоянство длины движущегося вектора служит выражением закона сохранения энергии. Рассмотрение биллиарда в области с гладкой границей позволяет получить содержательную информацию о спектре Дирихле задачи в такой области.
В зависимости от вида границы дQ выделяют неск. классов биллиардов с существенно разл. эргодич. свойствами, к-рые к настоящему времени (1997) изучены далеко не полностью.
Кое-что известно о биллиардах в многоугольниках и многогранниках, в частности то, что энтропия такого биллиарда равна нулю и что биллиард в большинстве прямоугольных треугольников эргодичен. Рассмотрим биллиард в n -угольнике с углами ai, к-рые соизмеримы с p(т. е. ai = lip/mi, где li mi- целые числа). Всякой траектории биллиарда отвечает её проекция на Q - ломаная линия L со звеньями, концы к-рых лежат на сторонах многоугольника. Вследствие соизмеримости всех ai с p угол между любым звеном ломаной L и горизонталью может принимать лишь значения вида j + (m/l)p, где l -наименьшее общее кратное чисел l1, ..., ln, целое число т зависит от рассматриваемого звена, а j - постоянно вдоль траектории и удовлетворяет условию 0<=j<p/l. Очевидно, j - инвариантная ф-ция, не являющаяся константой, а потому биллиард не эргодичен (тем не менее для каждой его траектории, кроме нек-рого множества нулевой меры, соответствующая ломаная L всюду плотна в Q).
Ещё "менее эргодичен" биллиард в выпуклой области с достаточно гладкой границей (простейшие примеры - круг и эллипс). У такого биллиарда всегда существуют каустики - гладкие кривые g, лежащие в Q и обладающие по отношению к любой из траекторий (точнее, к любой из их проекций) L тем свойством, что либо L и g не имеют общих точек, либо каждое звено ломаной L касается g. Для биллиарда в круге каустики - концентрич. окружность (рис. 5), для биллиарда в эллипсе-софокусные эллипсы и гиперболы.
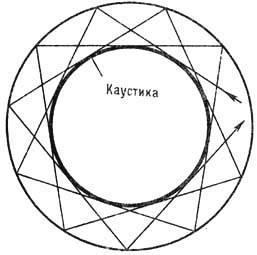
Рис. 5. Окружность - каустика биллиардной траектории в круге.
Наиб. содержательна Э. т. рассеивающих биллиардов (биллиардов Синая). У такого биллиарда граница состоит из конечного числа гладких кривых или многообразий большей размерности, строго выпуклых внутрь области Q (рис. 6). Эта граница, взятая в качестве зеркала, рассеивает (делает расходящимся) узкий параллельный пучок света, падающий на неё из Q. Рассеивающие биллиарды относятся к классу гиперболич. ДС с особенностями: преобразования, из к-рых состоит система, теряют свойство гладкости (и даже непрерывности) в нек-рых точках фазового пространства (при отражении от границы направление вектора скорости меняется скачком). Теория таких биллиардов во многом аналогична теории гладких гиперболич. систем, хотя и сложнее в техн. <отношении. Она приводит к выводу, что рассеивающий биллиард является К- и даже Б-системой. Следовательно, он обладает всеми стохастич. свойствами, характерными для таких систем. К-свойство обнаружено и у биллиардов в нек-рых областях, граница к-рых имеет как рассеивающие, так и фокусирующие и даже только одни фокусирующие участки. Примеры таких областей представлены на рис. 7. Среди них есть и выпуклые, но общей чертой всех границ является малая гладкость (по крайней мере, отсутствие второй производной).
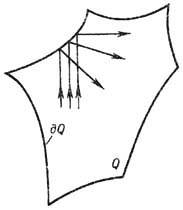
Рис. 6. Рассеивающий биллиард: параллельный пучок после отражения становится расходящимся.
Рис. 7. Примеры областей, в которых биллиард обладает К-свойством, хотя и не является рассеивающим.
Наряду с рассеивающими рассматриваются полурассеивающие биллиарды. У них граница дQ имеет размерность >=2 и состоит из гладких кусков Di , выпуклых, но не обязательно строго выпуклых внутрь Q: если пересечь Di к.-н. плоскостью П, проходящей через точку х
 Di , то для одних П получится выпуклая кривая, а для других- отрезок прямой (пример такого Di - боковая поверхность кругового цилиндра). Интерес к полурассеивающим биллиардам в значит. мере объясняется тем, что к ним сводится задача об эргодич. свойствах системы h упругих шаров в прямоугольном ящике, к-рая решена лишь при n<=4.
Di , то для одних П получится выпуклая кривая, а для других- отрезок прямой (пример такого Di - боковая поверхность кругового цилиндра). Интерес к полурассеивающим биллиардам в значит. мере объясняется тем, что к ним сводится задача об эргодич. свойствах системы h упругих шаров в прямоугольном ящике, к-рая решена лишь при n<=4.
Обнаружение стохастичности у биллиардных и подобных им систем опровергло существовавшее долгое время убеждение, что у ДС механич. происхождения такие свойства могут наблюдаться лишь при большом числе степеней свободы.
Одномерные динамические системы
В течение 70-х и 80-х гг. сформировался раздел Э. т., посвящённый изучению ДС с одномерным фазовым пространством, т. е. преобразований отрезка или окружности. Такие преобразования иногда возникают при рассмотрении ДС с более сложным фазовым пространством, но их значение в большей степени определяется др. факторами: красотой и глубиной самой теории одномерных отображений, её связями с такими областями математики, как теория чисел и комплексный анализ, и присутствием в ней ряда важных элементов, имеющих многомерный аналог. В то же время эта теория обладает спецификой, связанной в первую очередь с естественной упорядоченностью фазового пространства (наличием отношения "больше - меньше" между его точками), что часто позволяет при изучении одномерных отображений продвинуться гораздо дальше, чем в общем случае.
Простейший класс одномерных отображений, представляющий интерес для Э. т., состоит из кусочно-растягивающих отображений нек-рого отрезка [ а, b]. Каждое такое отображение задаётся кусочно-монотонной ф-цией, производная к-рой по абс. величине больше единицы всюду, где она определена. Более точно, это означает следующее. На [ а, b]можно найти такие точки x1< х2<...< х n, что при всех х, отличных от х0 = а, х1 ,..., х n, х п+1=b, существует производная f'( х), причём | f'(x)|>l, где l>1 (в точках xi ф-ция f не обязана даже быть непрерывной). Пример такого отображения отрезка [0, 1] можно задать ф-лой Tx = Fr(2x), где Fr, как и раньше, обозначает дробную часть числа. Здесь n=1, x1 = l/2 и отображение разрывно в точке 1/2. Это отображение имеет непосредственное отношение к разложению числа в двоичную дробь: если x = b1(x), b2( х), ... - такое разложение, то bn (Тх) = b п+1( х) п=1,2, ... . Близкий пример, в к-ром отображение уже всюду непрерывно, получится, если положить Тх=1 - |2 х- 1|, 0<= х<=1. Это т. <н. шатровое отображение (tent map) - термин, указывающий на форму его графика.
Иногда рассматривают кусочно-монотонные отображения более общего вида, когда число отрезков монотонности бесконечно, а производная может в отд. точках принимать значения 1 и - 1. Самый известный пример этого рода-преобразование Гаусса, определяемое на отрезке [0, 1] ф-лой Tx = Fr(f(x)), где f( х)= 1/ х при х
 0 и f(0) = 0. Тем самым Тх=1/х-п при 1/(п+1)<х<=1/п, все точки вида 1/п, п>1являются точками разрыва и, кроме того, f'(1) = - 1. Если преобразование из первого примера было связано с разложением в двоичную дробь, то для преобразования Гаусса ту же роль играет разложение в непрерывную (или цепную) дробь: пусть x = g1(x), g2(x) ... - такое разложение для х
0 и f(0) = 0. Тем самым Тх=1/х-п при 1/(п+1)<х<=1/п, все точки вида 1/п, п>1являются точками разрыва и, кроме того, f'(1) = - 1. Если преобразование из первого примера было связано с разложением в двоичную дробь, то для преобразования Гаусса ту же роль играет разложение в непрерывную (или цепную) дробь: пусть x = g1(x), g2(x) ... - такое разложение для х 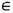 (0, 1); тогда, как и в первом примере, gn(Tx)=gn+1( х), п =1,2, .... Преобразование Гаусса существенно отличается по форме от первых двух примеров. Однако порождённые ими ДС имеют сходные эргодич. свойства по отношению к естественным инвариантным мерам. В первом и втором примерах такой мерой является обычная длина (мера Лебега), а в третьем - вероятностная мера m, к-рую можно задать нек-рой плотностью (т. е. m(dx)=p(x)dx). Инвариантность меры относительно преобразования Гаусса приводит к равенству p( х) = ((1+x) ln 2)-1.
(0, 1); тогда, как и в первом примере, gn(Tx)=gn+1( х), п =1,2, .... Преобразование Гаусса существенно отличается по форме от первых двух примеров. Однако порождённые ими ДС имеют сходные эргодич. свойства по отношению к естественным инвариантным мерам. В первом и втором примерах такой мерой является обычная длина (мера Лебега), а в третьем - вероятностная мера m, к-рую можно задать нек-рой плотностью (т. е. m(dx)=p(x)dx). Инвариантность меры относительно преобразования Гаусса приводит к равенству p( х) = ((1+x) ln 2)-1.
Абсолютно непрерывная инвариантная мера существует для весьма широкого класса кусочно-растягивающих отображений, хотя в общем случае невозможно указать явный вид её плотности. К упомянутому классу принадлежат, в частности, растягивающие отображения окружности. Отождествив окружность единичной длины с полуинтервалом [0, 1), можно задать такое отображение уже встречавшейся ф-лой Tx=Fr(f(x)), 0<= х<=1, где f -достаточно гладкая ф-ция, определённая на отрезке [0, 1 ] и удовлетворяющая условиям: f(0) = 0, f(1) - целое число и f'( х)>=l>1 (первый из приведённых выше примеров именно таков). При этих условиях существует абсолютно непрерывная T -инвариантная мера m с положительной плотностью; по отношению к этой мере Т является точным эндоморфизмом (см. выше), т. е. порождает полукаскад с сильными свойствами стохастичности; энтропия этой ДС равна
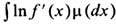
Большой интерес представляет изучение одномерных отображений, к-рые на одних участках являются растягивающими, а на других-сжимающими. Их свойства существенно зависят от того, как эти участки расположены вдоль траекторий отдельных точек. Примером может служить отображение Tx= 4x(1 - х),0<=x<=1, впервые рассмотренное Дж. фон Нейманом и С. Уггамом (S. Ulam) в сер. 40-х гг. Под действием этого отображения критич. точка х=1/2[в ней производная ф-ции 4 х(1 -х )равна нулю и, значит, в её окрестности происходит самое сильное сжатие] уже на первом шаге поглощается периодич. траекторией (состоящей из точек 1 и 0), в окрестности к-рой сжатие компенсируется постоянно действующим растяжением. Вследствие этого Т ведёт себя так же, как растягивающие отображения: существует абсолютно непрерывная T -инвариантная мера (с плотностью р(х) =p-1(x(1 - х))-1/2), относительно к-рой рассматриваемая ДС в высшей степени стохастична (изоморфна сдвигу Бернулли). Похожая картина наблюдается и в гораздо более общей ситуации. Если, в частности, рассмотреть однопараметрич. семейство отображений Tl = Fr(lf(x)), l>0, где ф-ция f в нек-ром смысле близка к квадратичной ф-ции х(1 -х), то для тех l, при к-рых действует аналогичный только что описанному компенсационный механизм, преобразование T стохастично. Оказывается, что множество таких l имеет положительную меру.
В 80-90-е гг. в теории одномерных отображений получили распространение методы, связанные с понятием ре-норм группы и с теорией КАМ (Колмогорова - Арнольда-Мозера). В целом одномерная динамика пока далека от завершения. Последнее в ещё большей степени относится к теории многомерных не всюду растягивающих отображений, к-рая делает только первые шаги.
Случайные динамические системы
Необходимость изучения случайных ДС, т. е. систем, зависящих от случайного параметра, обусловлена теми же причинами, что и применение вероятностных моделей вообще. Важную роль играет, в частности, то обстоятельство, что при численном моделировании приходится производить дискретизацию системы как по времени, так и по пространству, а также учитывать возможность случайных ошибок. В Э. т. имеется конструкция, позволяющая ценой расширения фазового пространства сводить нек-рые случайные ДС к неслучайным. Пусть, напр., задана стационарная случайная последовательность с действительными значениями { у n, n= 0, 1, ...} и при каждом п определено сохраняющее меру m преобразование Т yп пространства X, зависящее от случайной величины у n как от параметра. Последовательность случайных преобразований Т (п)=Т yп Т yn-1... Т у1 Т y0 естественно называть с л у ч а й н о й ДС. Для неё выполняется с л у ч а й н а я (по другой терминологии- вероятностная) э р г о д и ч. т е о р е м а: если f- интегрируемая ф-ция на X, то событие, состоящее в том, что при m-почти всех х
 X существует предел
X существует предел
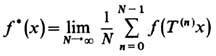
и что ф-ция f* интегрируема по мере m, имеет вероятность 1. Это утверждение сводится к индивидуальной эргодич. теореме для неслучайной ДС {
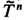 } в пространстве пар ( у, х), где х
} в пространстве пар ( у, х), где х X; у- бесконечная последовательность дей-ствит. чисел, а преобразование
X; у- бесконечная последовательность дей-ствит. чисел, а преобразование 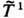 имеет "треугольный" вид:
имеет "треугольный" вид:  ( у, х) = (j( у), y(y, x) )где j-сдвиг в пространстве последовательностей. Преобразования такого вида, наз. косыми произведениями, встречаются в разл. областях Э. т.
( у, х) = (j( у), y(y, x) )где j-сдвиг в пространстве последовательностей. Преобразования такого вида, наз. косыми произведениями, встречаются в разл. областях Э. т.
Другой подход к определению случайной ДС основан на том, что преобразование Т у пространства X, зависящее от случайного параметра у, порождает на X марковский случайный процессxt с дискретным временем (цепь Маркова), у к-рого вероятность перехода за один шаг из точки х
 X в множество А
X в множество А  X равна вероятности того, что Т у х
X равна вероятности того, что Т у х  А. Этот марковский процесс и наз. случайной ДС. Если случайный параметр у в том или ином смысле близок к фикси-ров. значению у0, то процесс xt наз. малым случайным возмущением неслучайной ДС {Т t} = {Т t у0}. Это определение переносится на системы с непрерывным временем, для них процесс xt часто описывается дифференц. ур-ниями со случайным коэф. или дифференц. стохастическими уравнениями. Несколько иной тип малого случайного возмущения ДС - это марковский процесс, в к-ром случайная точка, выйдя из х, распределяется через единицу времени вблизи точки Т1 х. Центральная проблема теории малых случайных возмущений касается поведения инвариантной меры me соответствующего марковского процесса при стремлении к нулю величины возмущения, характеризуемой параметром e. Первоначально эта проблема изучалась для ДС с притягивающими неподвижными точками (положениями равновесия) или предельными циклами. В 70-х гг. началось исследование систем с гиперболич. аттракторами. Если при en
А. Этот марковский процесс и наз. случайной ДС. Если случайный параметр у в том или ином смысле близок к фикси-ров. значению у0, то процесс xt наз. малым случайным возмущением неслучайной ДС {Т t} = {Т t у0}. Это определение переносится на системы с непрерывным временем, для них процесс xt часто описывается дифференц. ур-ниями со случайным коэф. или дифференц. стохастическими уравнениями. Несколько иной тип малого случайного возмущения ДС - это марковский процесс, в к-ром случайная точка, выйдя из х, распределяется через единицу времени вблизи точки Т1 х. Центральная проблема теории малых случайных возмущений касается поведения инвариантной меры me соответствующего марковского процесса при стремлении к нулю величины возмущения, характеризуемой параметром e. Первоначально эта проблема изучалась для ДС с притягивающими неподвижными точками (положениями равновесия) или предельными циклами. В 70-х гг. началось исследование систем с гиперболич. аттракторами. Если при en 0 последовательность мер men сходится, то предельная мера, как правило, оказывается инвариантной мерой невозмущённой ДС. На гиперболич. аттракторе сосредоточено несчётное множество инвариантных мер, однако при нек-рых общих условиях me сходится лишь к одной из них, а именно к равновесному состоянию, отвечающему коэффициенту растяжения объёма на неустойчивом многообразии (см. ниже).
0 последовательность мер men сходится, то предельная мера, как правило, оказывается инвариантной мерой невозмущённой ДС. На гиперболич. аттракторе сосредоточено несчётное множество инвариантных мер, однако при нек-рых общих условиях me сходится лишь к одной из них, а именно к равновесному состоянию, отвечающему коэффициенту растяжения объёма на неустойчивом многообразии (см. ниже).
Э. т. и классическая статистическая физика
Э. т., обязанная своим возникновением статистической физике, долгое время развивалась самостоятельно и лишь в 1970-х гг. вновь испытала влияние идей статистич. физики. Причины этого - появление новых методов в самой Э. т., с одной стороны, и дальнейшая математизация статистич. физики-с другой.
Переосмысление понятия термодинамич. предельного перехода привело к общему определению гиббсовского случайного поля, иначе-гиббсовской меры, или Гиббса распределения, на фазовом пространстве бесконечной системы взаимодействующих частиц. Эта мера определяется своим гамильтонианом. В случае системы частиц с координатами qi
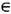 Rd, импульсами р j
Rd, импульсами р j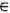 Rd, гамильтониан к-рой имеет вид
Rd, гамильтониан к-рой имеет вид
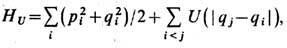
где U- потенциал попарного взаимодействия, она инвариантна относительно бесконечночастичной гамильтоно-вой ДС {Т tU}, отвечающей HU. В то же время никакая гиббсовская мера с гамильтонианом общего вида, отличным от HU , не является {T tU}-инвариантной [единственное нетривиальное исключение относится к потенциалу U(r) = a/sh2(br); а, b=const]. Этот факт согласуется с принципом необратимости и сходимости к равновесию, строгое обоснование к-рого, вообще говоря, возможно только для систем с бесконечным числом степеней свободы и в общем случае отсутствует.
Поток {Т tU} с инвариантной гиббсовской мерой наз. ДС статистич. механики. Её эргодич. свойства известны лишь для самых простых взаимодействий. Так, если U =0. (случай идеального газа неразличимых частиц), то {T tU} является Б-системой. Более содержательна др. бесконечномерная модель - газ Лоренца (Н. Lorentz), отличающаяся от модели идеального газа тем, что точечные частицы движутся не во всём пространстве Rd, а вне области, занимаемой бесконечным множеством d -мерных шаров (рассеива-телей), отражаясь от границы каждого шара по закону: "угол падения равен углу отражения". Упрощённый вариант этой модели, где имеется лишь одна движущаяся частица, а рассеиватели расположены периодически, сводится к рассеивающему биллиарду на d -мерном торе, из к-рого выброшено конечное число шаров. При d=2. для соответствующего потока {Т t} и ф-ции q(x), задающей координату q точки x=(q, p )фазового пространства, доказано, что случайный процесс
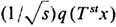 , рассматриваемый на любом конечном интервале времени 0<=t<=t0, сходится при s-> со к броуновскому движению и что существует положит. коэф. диффузии, выражаемый через корреляционную функцию скорости движущейся частицы. Это первый пример, в к-ром броуновское движение строго выводится из чисто детерминиров. динамики.
, рассматриваемый на любом конечном интервале времени 0<=t<=t0, сходится при s-> со к броуновскому движению и что существует положит. коэф. диффузии, выражаемый через корреляционную функцию скорости движущейся частицы. Это первый пример, в к-ром броуновское движение строго выводится из чисто детерминиров. динамики.
Для случая, когда в той же ситуации движется бесконечное множество частиц, доказано, что соответствующий поток является К-системой. Природа стохастичности этой системы иная, чем у идеального газа. В самом деле, в отличие от модели Лоренца, в движении отд. частицы идеального газа нет никакой стохастичности и, т. к. частицы друг с другом не взаимодействуют, стохастичность всей системы выглядит парадоксально, по крайней мере, она не согласуется с общепринятым представлением, что в основе этого свойства должна лежать нетривиальность взаимодействия. В случае же идеального газа причиной стохастичности служат бесконечность числа частиц и их неразличимость- при отказе от любого из этих условий стохастичность исчезает (впрочем, неразличимость частиц, вследствие к-рой координата и скорость отд. частицы не являются ф-циями на фазовом пространстве, можно считать суррогатом взаимодействия).
Другая идея статистич. физики, оказавшая влияние на Э. <т.,- это вариационный принцип Гиббса, согласно к-ро-му гиббсовская мера характеризуется макс. значением энтропии при фиксиров. средней энергии. Для одномерной решёточной спиновой модели его точная формулировка такова. Пусть X- пространство последовательностей x = {xi , -
 <i<
<i< }, xi=b1, и S -определённое на нём преобразование сдвига, т. <е. (X, S) - символич. ДС, для к-рой инвариантная мера пока не выбрана. На множестве всех S -инвариантных вероятностных мер m вводится функционал
}, xi=b1, и S -определённое на нём преобразование сдвига, т. <е. (X, S) - символич. ДС, для к-рой инвариантная мера пока не выбрана. На множестве всех S -инвариантных вероятностных мер m вводится функционал
где hm - энтропия каскада {S t} (для этой и др. дискретных моделей статистич. физики величина, соответствующая энтропии Гиббса, совпадает с hm), а j(x) - энергия взаимодействия спина в нулевой точке решётки
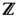 со всеми остальными спинами. Вариационный принцип для рассматриваемой бесконечной модели гласит, что гиббсовские меры, отвечающие заданному взаимодействию, и только они максимизируют функционал F(m)[при этом mах F(m) есть термодинамич. предел логарифма статистической суммы]. Если взаимодействие достаточно быстро убывает на бесконечности, то существует только одна гиббсовская мера и по отношению к ней S является Б-системой.
со всеми остальными спинами. Вариационный принцип для рассматриваемой бесконечной модели гласит, что гиббсовские меры, отвечающие заданному взаимодействию, и только они максимизируют функционал F(m)[при этом mах F(m) есть термодинамич. предел логарифма статистической суммы]. Если взаимодействие достаточно быстро убывает на бесконечности, то существует только одна гиббсовская мера и по отношению к ней S является Б-системой.
Очевидно, функционал F(m)имеет смысл для любой ДС и любой ограниченной ф-ции j, заданной на её фазовом пространстве. Обычно ф предполагается непрерывной ф-цией, тогда sup F(m)по всем инвариантным мерам можно определить в чисто топологич. терминах без помощи каких-либо мер на фазовом пространстве. По аналогии со спец. случаем, рассмотренным выше, эта верхняя грань наз. топологич. давлением (при j = 0 это не что иное, как топологич. энтропия), а меры, на к-рых она достигается, наз. равновесными состояниями, отвечающими j. Однако в общем случае равновесные состояния могут и не существовать (даже при j = 0).
Особенно полезно рассмотрение равновесных состояний в случае гиперболич. ДС. В частности, инвариантная мера на гиперболич. аттракторе, к к-рой сходятся ср. арифметические сдвигов риманова объёма, служит равновесным состоянием для ф-ции j, равной в каждой точке х логарифму локального коэф. растяжения kU(x )риманова объёма на неустойчивом многообразии, проходящем через x [kU(x )выражается через характеристические показатели]. Этот факт вытекает из анализа достаточно простой символич. модели (фактор-системы), к-рая существует у рассматриваемой ДС.
Приём, близкий к термодинамич. предельному переходу, используется при изучении фрактальной структуры (см. Фракталы )инвариантных множеств ДС и в нек-рых др. задачах. Весь этот круг идей получил название т е р м о д ин а м и ч е с к о г о ф о р м а л и з м а.
Некоммутативная Э. т.
Большая часть материала предыдущих разделов может быть изложена без обращения к фазовому пространству ДС, а с использованием вместо него тех или иных пространств ф-ций, заданных на X, напр. пространства
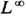 ограниченных измеримых комплекснозначных ф-ций. Это пространство допускает наряду с линейными операциями также операцию перемножения любых двух его элементов и операцию комплексного сопряжения. Тем самым оно является С * -алгеброй, к-рая коммутативна, т. <к. этим свойством обладает операция умножения. Всякая мера m, заданная на X, определяет на этой алгебре положит. линейный функционал (состояние) rm, к-рый ставит в соответствие ф-ции f число
ограниченных измеримых комплекснозначных ф-ций. Это пространство допускает наряду с линейными операциями также операцию перемножения любых двух его элементов и операцию комплексного сопряжения. Тем самым оно является С * -алгеброй, к-рая коммутативна, т. <к. этим свойством обладает операция умножения. Всякая мера m, заданная на X, определяет на этой алгебре положит. линейный функционал (состояние) rm, к-рый ставит в соответствие ф-ции f число  задаёт группу {U t} её автоморфизмов по ф-ле (U tf)(x)=f(Utx). Если m-инвариантная мера, то, очевидно, функционал rm инвариантен относительно этой группы: rm(U t f) = rm(f).
задаёт группу {U t} её автоморфизмов по ф-ле (U tf)(x)=f(Utx). Если m-инвариантная мера, то, очевидно, функционал rm инвариантен относительно этой группы: rm(U t f) = rm(f).
Описанный алгебраич. подход применим и в некоммутативном случае. Ему соответствует определение ДС как однопараметрич. группы автоморфизмов {t t} нек-рой С * -алгебры
 , на к-рой задано состояние r, инвариантное относительно этой группы. Подобные объекты появляются в квантовой статистич. механике, в частности при определении равновесных состояний (КМШ-состояний), и в квантовой теории поля. Их изучение составляет предмет некоммутативной Э. <т., основы к-рой были заложены Дж. фон Нейманом и И. Сигалом (I. Segal).
, на к-рой задано состояние r, инвариантное относительно этой группы. Подобные объекты появляются в квантовой статистич. механике, в частности при определении равновесных состояний (КМШ-состояний), и в квантовой теории поля. Их изучение составляет предмет некоммутативной Э. <т., основы к-рой были заложены Дж. фон Нейманом и И. Сигалом (I. Segal).
На некоммутативные ДС обобщаются многие понятия и факты Э. т., в т. ч. статистич. и индивидуальная эргодич. теоремы, имеющие дело со сходимостью средних
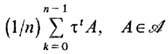
(случай дискретного времени), а также теорема о разложении на эргoдич. компоненты и понятие перемешивания. Однако непосредств. обобщение возможно далеко не всегда. Так, в формулировке индивидуальной эргодич. теоремы фигурирует сходимость почти всюду - свойство, непосредственно связанное с фазовым пространством. Перенести это понятие на некоммутативный случай позволяет тот факт, что сходимость почти всюду равносильна равномерной сходимости вне множества произвольно малой меры (т е о р е м а Е г о р о в а). Намного сложнее, чем в коммутативном случае, определяется энтропия некоммутативной ДС. Имеются также некоммутативные аналоги К-систем. В целом некоммутативная Э. т. имеет гораздо менее завершённый вид, чем её коммутативный прототип.
Лит.: Халмош П., Лекции по эргодической теории, пер. с англ., М., 1959; Биллингслей П., Эргодическая теория и информация, пер. с англ., М., 1969; Алексеев В. М., Символическая динамика, в кн.: 11-я математическая школа. АН УССР, К., 1976; Орнстейн Д., Эргодическая теория, случайность и динамические системы, пер. с англ., М., 1978; Боуэн Р., Методы символической динамики, пер. с англ., М., 1979; Корнфельд И. П., Синай Я. Г., Фомин С. В., Эргодическая теория, М., 1980; Брат-тел и У., Робинсон Д., Операторные алгебры и квантовая статистическая механика, пер. с англ., М., 1982; Peterson К., Ergodic theory, Cambridge, 1983; Заславский Г. М., Стохастичность динамических систем, М., 1984; Итоги науки и техники, сер. Современные проблемы математики. Фундаментальные направления, т. 2, М., 1985; Темпельман А. А., Эргодические теоремы на группах, Вильнюс, 1986; Мартин Н., Ингленд Дж., Математическая теория энтропии, пер. с англ., М., 1988; Гальперин Г. А., Земляков А. Н., Математические бильярды, М., 1990; Синай
Я. Г., Современные проблемы эргодической теории, М., 1995; KatokA., Hasselblatt B., Introduction to the theory of dynamical systems, Cambridge, 1995. Б. М. Гуревич.
Физическая энциклопедия. В 5-ти томах. — М.: Советская энциклопедия. Главный редактор А. М. Прохоров. 1988.
.
