- Нижний предел
-
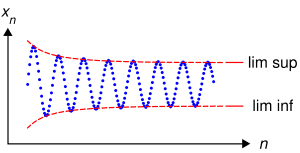 Верхний предел (lim sup) и нижний предел (lim inf) последовательности.
Верхний предел (lim sup) и нижний предел (lim inf) последовательности.Частичным пределом последовательности называется предел какой-либо её подпоследовательности, если существует хотя бы одна подпоследовательность, имеющая предел. Очевидно, что только предельная точка множества элементов последовательности может быть её частичным пределом, а также обратное (для доказательства будем брать δn = 1 / n и, выбирая в каждой δ-окрестности предельной точки член последовательности, построим таким образом сходящуюся к этой точке подпоследовательность).
Нижним пределом последовательности (обозначается
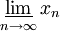 или
или 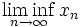 ) называется наименьший элемент множества частичных пределов последовательности, а верхним пределом (
) называется наименьший элемент множества частичных пределов последовательности, а верхним пределом (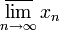 или
или 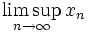 ) — наибольший элемент.
) — наибольший элемент.Не во всяком множестве существуют наибольший или наименьший элемент; примером может служить интервал (0,1). Однако утверждается, что у ограниченной последовательности верхний и нижний пределы существуют.
Докажем это утверждение для верхнего предела. По теореме Больцано — Вейерштрасса множество частичных пределов ограниченной последовательности непусто. Пусть s — верхняя грань множества A частичных пределов. Тогда заметим, что
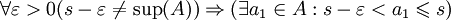 , а это означает, что в любой окрестности точки a1 находится бесконечно много членов последовательности. Поскольку утверждение верно для любого
, а это означает, что в любой окрестности точки a1 находится бесконечно много членов последовательности. Поскольку утверждение верно для любого  , мы можем сказать, что в любой окрестности точки s содержится бесконечно много членов последовательности (так как в любой окрестности мы можем найти точку a1). Значит, s по определению является предельной точкой последовательности, а стало быть, и её частичным пределом, что и требовалось доказать. Аналогично доказывается случай нижнего предела.
, мы можем сказать, что в любой окрестности точки s содержится бесконечно много членов последовательности (так как в любой окрестности мы можем найти точку a1). Значит, s по определению является предельной точкой последовательности, а стало быть, и её частичным пределом, что и требовалось доказать. Аналогично доказывается случай нижнего предела.Последовательность {xn} сходится к a тогда и только тогда, когда
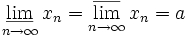 , так как получается, что a — единственная предельная точка множества элементов последовательности.
, так как получается, что a — единственная предельная точка множества элементов последовательности.
Wikimedia Foundation. 2010.
