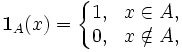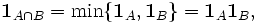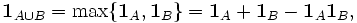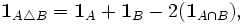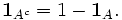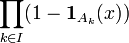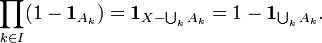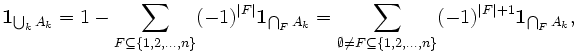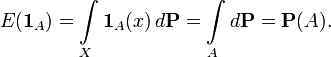Характеристическая функция множества

Индикатор, или характеристическая функция, или индикаторная функция подмножества 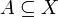$A \subseteq X$ — это функция, определенная на множестве X, которая указывает на принадлежность элемента $x \in X$ подмножеству A.

Термин характеристическая функция уже занят в теории вероятностей. По этой причине, почти исключительно одни вероятностники используют термин индикаторная функция для определяемой здесь функции, в то время как математикам из других областей для описания принадлежности элементов множеству больше нравится использовать термин характеристическая функция.

Определение

Пусть 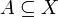$A\subseteq X$ — выбранное подмножество произвольного множества X. Функция 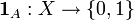$\mathbf{1}_A:X\to\{0,1\}$, определенная следующим образом:

$\mathbf{1}_A(x) = \left\{\begin{matrix} 1, &x \in A, \\ 0, &x \notin A, \end{matrix}\right.$

называется индикатором множества A.

Альтернативными обозначениями индикатора множества A являются: χ_A или 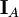$\mathbf{I}_A$, а иногда даже A(x). Скобка Иверсона позволяет обозначение $[x \in A]$.

(Греческая буква χ происходит от начальной буквы греческого написания слова характеристика.)

Предупреждение. Обозначение 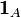$\mathbf{1}_A$ может означать функцию идентичности.

Основные свойства

Отображение, которое связывает подмножество 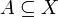$A \subseteq X$ с его индикатором 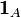$\mathbf{1}_A$ инъективно. Если A и B — два подмножества 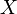$X \$, то

$\mathbf{1}_{A\cap B} = \min\{\mathbf{1}_A,\mathbf{1}_B\} = \mathbf{1}_A \mathbf{1}_B,$

$\mathbf{1}_{A\cup B} = \max\{{\mathbf{1}_A,\mathbf{1}_B}\} = \mathbf{1}_A + \mathbf{1}_B - \mathbf{1}_A \mathbf{1}_B,$

$\mathbf{1}_{A\triangle B} = \mathbf{1}_A + \mathbf{1}_B - 2(\mathbf{1}_{A\cap B}),$

$\mathbf{1}_{A^c} = 1-\mathbf{1}_A.$

Более общо, предположим 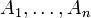$A_1,\ldots, A_n$ — это набор подмножеств X. Ясно, что для любого $x \in X$

$\prod_{k \in I} ( 1 - \mathbf{1}_{A_k}(x))$

— произведение нулей и единиц. Это произведение принимает значение 1 точно для тех $x \in X$, которые не принадлежат ни одному множеству A_k и 0 иначе. Поэтому

$\prod_{k \in I} ( 1 - \mathbf{1}_{A_k}) = \mathbf{1}_{X - \bigcup_{k} A_k} = 1 - \mathbf{1}_{\bigcup_{k} A_k}.$

Разворачивая левую часть, получаем

$\mathbf{1}_{\bigcup_{k} A_k}= 1 - \sum_{F \subseteq \{1, 2, \ldots, n\}} (-1)^{|F|} \mathbf{1}_{\bigcap_F A_k} = \sum_{\emptyset \neq F \subseteq \{1, 2, \ldots, n\}} (-1)^{|F|+1} \mathbf{1}_{\bigcap_F A_k},$

где | F | — мощность F. Это одна из форм принципа включения-исключения. Этот пример указывает, что индикатор — полезное обозначение в комбинаторике, которое используется также и в других областях, например в теории вероятностей: если X — вероятностное пространство с вероятностной мерой 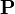$\mathbf{P}$, а A — измеримое множество, то индикатор 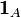$\mathbf{1}_A$ становится случайной величиной, чье математическое ожидание равно вероятности A:

$E(\mathbf{1}_A)= \int\limits_{X} \mathbf{1}_A(x)\,d\mathbf{P} = \int\limits_{A} d\mathbf{P} = \mathbf{P}(A).\quad$

Это тождество используется в простых доказательствах неравенства Маркова.

Библиография

• Folland, G.B.; Real Analysis: Modern Techniques and Their Applications, 2nd ed, John Wiley & Sons, Inc., 1999.
• Thomas H. Cormen, Charles E. Leiserson, Ronald L. Rivest, and Clifford Stein. Introduction to Algorithms, Second Edition. MIT Press and McGraw-Hill, 2001. ISBN 0-262-03293-7. Section 5.2: Indicator random variables, pp.94–99.

См. также

• Простая функция
• Функция принадлежности