Характеристическая функция (нечёткая логика)

Функция принадлежности нечёткого множества — это обобщение индикаторной (или характеристической) функции классического множества. В нечёткой логике она представляет степень принадлежности каждого члена пространства рассуждения к данному нечёткому множеству. Степени принадлежности часто смешивают с вероятностями, хотя они принципиально отличны.

Определение

Для пространства рассуждения $\mathbf{X} \$ и данной функции принадлежности $\mu : \mathbf{X} \to [0,1]$ нечёткое множество определяется как

$\tilde{\mathit{A}}=\{(x,\mu_{A}(x))\mid x\in\mathbf{X}\}.$

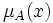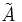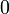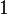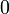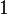Функция принадлежности $\mu_{A}(x) \$ количественно градуирует приналежность элементов фундаментального множества пространства рассуждения $x \in \mathbf{X}$ нечёткому множеству $\tilde{\mathit{A}}$. Значение $0 \$ означает, что элемент не включен в нечёткое множество, $1 \$ описывает полностью включенный элемент. Значения между $0 \$ и $1 \$ характеризуют нечётко включенные элементы.

Нечёткое множество и классическое, четкое (crisp) множество

Классификация функций принадлежности нормальных нечетких множеств

Нечеткое множество называется нормальным, если для его функции принадлежности 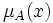$\mu_{A}(x) \$ справедливо утверждение, что существует такой $x\in\mathbf{X}$, при котором $\mu_{A}(x)=1 \$.

Функция принадлежности класса s

Функция принадлежности класса s определяется как:

$s \left( x;a,b,c \right)= \left\{\begin{matrix} 0, & x \leqslant a, \\ 2\left({{x-a}\over{c-a}}\right)^2, & a \leqslant x \leqslant b, \\ 1-2\left({{x-c}\over{c-a}}\right)^2, & b \leqslant x \leqslant c, \\ 1, & x \geqslant c, \end{matrix}\right.$

где $b = {{a + c}\over {2}}$.

Функция принадлежности класса π

Функция принадлежности класса π определяется через функцию класса s:

$\pi \left( x;a,b,c \right)= \left\{\begin{matrix} s \left( x;c-b,c-{b \over 2},c \right), & x \leqslant c, \\ 1- s \left( x;c,c+{b \over 2},c+b \right), & x \geqslant c, \end{matrix}\right.$

где $b = {{a + c}\over {2}}$.

Функция принадлежности класса γ

Функция принадлежности класса γ определяется как:

$\gamma \left( x;a,b \right)= \left\{\begin{matrix} 0, & x \leqslant a , \\ {{x-a}\over {b-a}}, & a \leqslant x \leqslant b, \\ 1, & x \geqslant b, \end{matrix}\right.$

Функция принадлежности класса t

Функция принадлежности класса t определяется как:

$t \left( x;a,b,c \right)= \left\{\begin{matrix} 0, & x \leqslant a , \\ {{x-a}\over {b-a}}, & a \leqslant x \leqslant b, \\ {{c-x}\over {c-b}}, & b \leqslant x \leqslant c, \\ 1, & x \geqslant c, \end{matrix}\right.$

Функция принадлежности класса L

Функция принадлежности класса L определяется как:

$L \left( x;a,b \right)= \left\{\begin{matrix} 1, & x \leqslant a , \\ {{b-x}\over {b-a}}, & a \leqslant x \leqslant b, \\ 0, & x \geqslant b, \end{matrix}\right.$

См. также

• Теория нечёткой меры
• Операции над нечеткими множествами
• Грубое множество
• Эвентология

Внешние ссылки

• Fuzzy Image Processing

Литература

1. Д. Рутковская, М. Пилиньский, Л. Рутковский. Нейронные сети, генетические алгоритмы и нечеткие системы: Пер. с польского И. Д. Рудинского. — М.:Горячая линия — Телеком, 2004. — 452 с — ISBN 5-93517-103-1