Формула Шварца — Кристоффеля
- Формула Шварца — Кристоффеля
-
Теорема Шварца — Кристоффеля — важная теорема в теории функций комплексного переменного, носит название немецких математиков Карла Шварца и Элвина Кристоффеля.
Очень важной с практической точки зрения является проблема о конформном отображении некой канонической области (единичного круга Δ или верхней полуплоскости 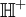 ) на внутренность произвольного многоугольника. Важность следующей теоремы в том, что она дает общий вид таких отображений.
) на внутренность произвольного многоугольника. Важность следующей теоремы в том, что она дает общий вид таких отображений.
Теорема
Предположим, что 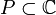 — некоторый n-угольник, а функция f осуществляет конформное отображение
— некоторый n-угольник, а функция f осуществляет конформное отображение 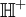 на P. Тогда f можно представить в виде
на P. Тогда f можно представить в виде
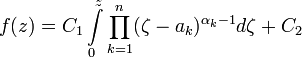 ,
,
где 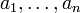 — прообразы вершин P на вещественной оси,
— прообразы вершин P на вещественной оси, 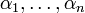 — радианные меры соответствующих внутренних углов, а C1 и C2 — так называемые акцессорные параметры. Интеграл в правой части имеет собственное название — его называют интегралом Шварца — Кристоффеля I рода.
— радианные меры соответствующих внутренних углов, а C1 и C2 — так называемые акцессорные параметры. Интеграл в правой части имеет собственное название — его называют интегралом Шварца — Кристоффеля I рода.
В случае, если прообраз одной из вершин многоугольника находится в бесконечности, то формула немного видоизменяется. Если n-ая вершина имеет своим прообразом бесконечно удалённую точку, то формула будет иметь вид
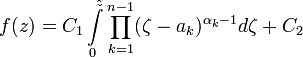 ,
,
то есть множитель, соответствующий этой вершине, будет просто отсутствовать. Такой интеграл будет интегралом Шварца — Кристоффеля II рода.
Трудность использования этих формул состоит в том, что точки 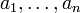 , как и акцессорные параметры, в общем случае неизвестны. Для их вычисления обычно на многоугольник накладываются какие-то дополнительные нормировки, либо вычисление производится приближённо (что применяется на практике).
, как и акцессорные параметры, в общем случае неизвестны. Для их вычисления обычно на многоугольник накладываются какие-то дополнительные нормировки, либо вычисление производится приближённо (что применяется на практике).
Wikimedia Foundation.
2010.
Полезное
Смотреть что такое "Формула Шварца — Кристоффеля" в других словарях:
КРИСТОФФЕЛЯ - ШВАРЦА ФОРМУЛА — формула дающая интегральное представление функции f(z), конформно отображающей верхнюю полуплоскость на внутренность ограниченного многоугольника с вершинами и углами при вершинах < . При этом некоторые постоянные, Постоянную z0 можно… … Математическая энциклопедия
Отображение Шварца — Кристоффеля — Теорема Шварца Кристоффеля важная теорема в теории функций комплексного переменного, носит название немецких математиков Карла Шварца и Элвина Кристоффеля. Очень важной с практической точки зрения является проблема о конформном… … Википедия
Отображение Шварца — Теорема Шварца Кристоффеля важная теорема в теории функций комплексного переменного, носит название немецких математиков Карла Шварца и Элвина Кристоффеля. Очень важной с практической точки зрения является проблема о конформном… … Википедия
Теорема Шварца — Кристоффеля — Теорема Шварца Кристоффеля важная теорема в теории функций комплексного переменного, носит название немецких математиков Карла Шварца и Элвина Кристоффеля. Очень важной с практической точки зрения является проблема о конформном отображении… … Википедия
Интеграл Шварца — Кристоффеля — Теорема Шварца Кристоффеля важная теорема в теории функций комплексного переменного, носит название немецких математиков Карла Шварца и Элвина Кристоффеля. Очень важной с практической точки зрения является проблема о конформном отображении… … Википедия
Шварц, Карл Герман Амандус — В Википедии есть статьи о других людях с такой фамилией, см. Шварц. Карл Герман Амандус Шварц нем. Karl Hermann Amandus Schwarz … Википедия
КОНФОРМНОЕ ОТОБРАЖЕНИЕ — взаимно однозначное отображение областей n мерного евклидова пространства, сохраняющее углы между кривыми. К. о. в каждой точке обладает свойством постоянства растяжений по разл. направлениям. При n= З любое (гладкое) К. о. является суперпозицией … Физическая энциклопедия
ВЫПУКЛАЯ ФУНКЦИЯ — комплексного переменногог регулярная однолистная функция в единичном круге , отображающая единичный круг на нек рую выпуклую область. Регулярная однолистная функция является В. ф. тогда и только тогда, когда при обходе любой окружности… … Математическая энциклопедия
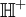 ) на внутренность произвольного многоугольника. Важность следующей теоремы в том, что она дает общий вид таких отображений.
) на внутренность произвольного многоугольника. Важность следующей теоремы в том, что она дает общий вид таких отображений.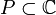 — некоторый n-угольник, а функция f осуществляет конформное отображение
— некоторый n-угольник, а функция f осуществляет конформное отображение 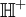 на P. Тогда f можно представить в виде
на P. Тогда f можно представить в виде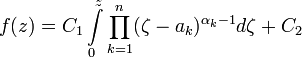 ,
,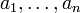 — прообразы вершин P на вещественной оси,
— прообразы вершин P на вещественной оси, 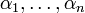 — радианные меры соответствующих внутренних углов, а C1 и C2 — так называемые акцессорные параметры. Интеграл в правой части имеет собственное название — его называют интегралом Шварца — Кристоффеля I рода.
— радианные меры соответствующих внутренних углов, а C1 и C2 — так называемые акцессорные параметры. Интеграл в правой части имеет собственное название — его называют интегралом Шварца — Кристоффеля I рода.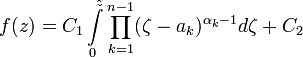 ,
,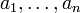 , как и акцессорные параметры, в общем случае неизвестны. Для их вычисления обычно на многоугольник накладываются какие-то дополнительные нормировки, либо вычисление производится приближённо (что применяется на практике).
, как и акцессорные параметры, в общем случае неизвестны. Для их вычисления обычно на многоугольник накладываются какие-то дополнительные нормировки, либо вычисление производится приближённо (что применяется на практике).