- КОНФОРМНОЕ ОТОБРАЖЕНИЕ
- КОНФОРМНОЕ ОТОБРАЖЕНИЕ
-
- взаимно однозначное отображение областей n -мерного евклидова пространства, сохраняющее углы между кривыми. К. о. в каждой точке обладает свойством постоянства растяжений по разл. направлениям. При n= З любое (гладкое) К. о. является суперпозицией вращения, растяжения, сдвига и спец. К. о. "инверсии": х i - ( х i -х i)/
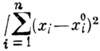 ,
, i = l,. . ., п, где ,х°=(х 01, . .., х0 п) - нек-рая фиксированная точка n -мерного пространства. Совокупность этих преобразований образует (n+1) (n+2)/2-параметрич. конформную группу.
При n=2 множество К. о. разнообразнее. В этом случае двумерную плоскость R2 удобно реализовать как пространство С комплексных чисел z=x+iy. Добавляя к С бесконечно удалённую точку, рассматривают также К. о. областей расширенной комплексной плоскости
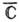 . Отображение области D на область D* расширенной комплексной плоскости
. Отображение области D на область D* расширенной комплексной плоскости 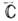 конформно тогда и только тогда, когда оно либо задаётся нек-рой аналитической функцией f(z), определённой и однолистной в D, и такой, что
конформно тогда и только тогда, когда оно либо задаётся нек-рой аналитической функцией f(z), определённой и однолистной в D, и такой, что 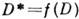 , либо является суперпозицией описанного преобразования и комплексного сопряжения. В первом случае К. о. сохраняет не только величины углов, но и их знаки; во-втором - знаки углов меняются на противоположные. Любые две односвязные области D и D* в
, либо является суперпозицией описанного преобразования и комплексного сопряжения. В первом случае К. о. сохраняет не только величины углов, но и их знаки; во-втором - знаки углов меняются на противоположные. Любые две односвязные области D и D* в 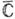 , границы к-рых состоят из более чем одной точки, конформно эквивалентны. При этом для произвольных точек z0 из D и
, границы к-рых состоят из более чем одной точки, конформно эквивалентны. При этом для произвольных точек z0 из D и 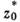 из
из 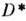 и произвольного вещественного числа
и произвольного вещественного числа 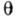 существует одна и только одна аналитич. и однолистная в D ф-ция f(z), такая, что f(D)=D*, f(z0)=z*0, arg
существует одна и только одна аналитич. и однолистная в D ф-ция f(z), такая, что f(D)=D*, f(z0)=z*0, arg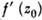 =
=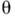 (теорема Римана).
(теорема Римана).
К. о. двумерных областей переводит всякое решение Лапласа уравнения снова в решение ур-ния Лапласа. Другими словами, если
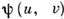 - гармонич. ф-ция в области D*, а ф-ция f(z) = u(x, y)+i
- гармонич. ф-ция в области D*, а ф-ция f(z) = u(x, y)+i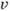 (x, у )конформно отображает область D на D*, то ф-ция
(x, у )конформно отображает область D на D*, то ф-ция 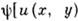 ,
, 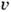 ( х, у)]есть гармонич. ф-ция в области D. Этим обусловлено применение К. о. в задачах электростатики, гидро- и аэродинамики и др.
( х, у)]есть гармонич. ф-ция в области D. Этим обусловлено применение К. о. в задачах электростатики, гидро- и аэродинамики и др.
Примеры. 1) Дробно-линейное преобразование f(z) = (az+b)/(cz+d), ad-be
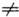 0 конформно отображает расширенную комплексную плоскость
0 конформно отображает расширенную комплексную плоскость 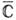 на себя. При этом всякая окружность переходит снова в окружность (считается, что прямая есть окружность бесконечного радиуса, проходящая через бесконечно удалённую точку). Тем самым дробно-линейное преобразование конформно отображает внутренность любого круга на внутренность или внешность нек-рого другого круга. Точки z и z* наз. сопряжёнными к окружности Г, не являющейся прямой, если они лежат на одном луче, исходящем из центра окружности, и произведение их расстояний от центра равно квадрату радиуса. Если Г - прямая, то точки z и z* наз. сопряжёнными, если одна из них переходит в другую при отражении относительно Г. Всякое дробно-линейное преобразование переводит точки z и z*, сопряжённые относительно Г, в точки f(z) и f(z*), сопряжённые относительно f (Г). Последнее свойство весьма полезно при выборе конкретных дробно-линейных преобразований.
на себя. При этом всякая окружность переходит снова в окружность (считается, что прямая есть окружность бесконечного радиуса, проходящая через бесконечно удалённую точку). Тем самым дробно-линейное преобразование конформно отображает внутренность любого круга на внутренность или внешность нек-рого другого круга. Точки z и z* наз. сопряжёнными к окружности Г, не являющейся прямой, если они лежат на одном луче, исходящем из центра окружности, и произведение их расстояний от центра равно квадрату радиуса. Если Г - прямая, то точки z и z* наз. сопряжёнными, если одна из них переходит в другую при отражении относительно Г. Всякое дробно-линейное преобразование переводит точки z и z*, сопряжённые относительно Г, в точки f(z) и f(z*), сопряжённые относительно f (Г). Последнее свойство весьма полезно при выборе конкретных дробно-линейных преобразований.
2) Степенная функция
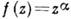 , где
, где 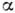 - положительное число, конформно отображает сектор
- положительное число, конформно отображает сектор 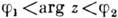 в сектор
в сектор 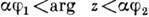 , если
, если 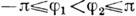 и
и 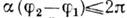 При нарушении последнего неравенства ф-ция / (z) перестаёт быть однолистной в секторе
При нарушении последнего неравенства ф-ция / (z) перестаёт быть однолистной в секторе
3)
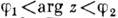 Показательная ф-ция f(z)=ez конформно отображает полосу
Показательная ф-ция f(z)=ez конформно отображает полосу 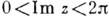 в единичный круг с разрезом вдоль вещественной положит. полуоси. При этом прямая Im z = j переходит в луч arg
в единичный круг с разрезом вдоль вещественной положит. полуоси. При этом прямая Im z = j переходит в луч arg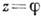
4) Функция Жуковского
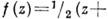
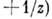 конформно отображает внешность единичного круга на внешность отрезка [-1, 1] вещественной оси. При этом окружность
конформно отображает внешность единичного круга на внешность отрезка [-1, 1] вещественной оси. При этом окружность 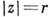 переходит в эллипс с полуосями
переходит в эллипс с полуосями 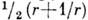 и
и 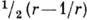 и с фокусами в точках
и с фокусами в точках 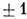
5) Формула Кристоффеля - Шварца даёт интегральное представление ф-ции f(z), отображающей верх. полуплоскость Im z>0 на внутренность многоугольника с вершинами Ak и углами при вершинах
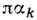 (k = 1, 2, . . .,n):
(k = 1, 2, . . .,n):
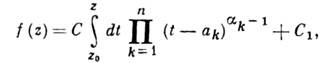
где С, С1 - комплексные постоянные, ak - действит. числа,
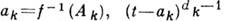 - однозначные при Im t>0 ветви ф-ций, положительные при t=ak; z0<a1, и точка f(z0)=C1 лежит на отрезке А n А1. Тройку чисел из <Лит. см. при ст. Аналитическая функция.
- однозначные при Im t>0 ветви ф-ций, положительные при t=ak; z0<a1, и точка f(z0)=C1 лежит на отрезке А n А1. Тройку чисел из <Лит. см. при ст. Аналитическая функция.
Б. И. Завьялов.
Физическая энциклопедия. В 5-ти томах. — М.: Советская энциклопедия. Главный редактор А. М. Прохоров. 1988.
.
