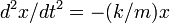Уравнения движения

Уравнение движения (уравнения движения) — уравнение или система уравнений, задающие закон эволюции механической или сходной динамической системы (например, поля) во времени^[1].

Эволюция физической системы однозначно определяется уравнениями движения и начальными условиями.

Введение

В уравнения движения динамической системы входит полный набор переменных, определяющий состояние этой системы (например, все координаты и скорости, или все координаты и импульсы), а также их производные по времени, что позволяет, зная такой набор в некий момент времени, вычислить его для момента времени, отстоящего на малый (бесконечно малый) промежуток времени. В принципе, повторяя этот процесс вычичления последовательно большое (бесконечное) количество раз, можно вычислить значение всех этих переменных для момента времени, как угодно^[2] далеко отстоящего от начального. С помощью такого процесса можно (выбрав Δt достаточно малым, но конечным) можно получить приближенное численное решение уравнений движения. Однако чтобы получить точное ^[3] решение, приходится применять другие математические методы.

В современной квантовой теории термин уравнение движения нередко используется для обозначения именно только классических уравнений движения, то есть как раз для различения классического и квантового случая. В таком употреблении, например, слова «решение уравнений движения» означают именно классическое (неквантовое) приближение, которое может затем так или иначе использоваться при получении квантового результата или для сравнения с ним. В этом смысле уравнения эволюции волновой функции не называют уравнениями движения, например упомянутые ниже уравнение Шредингера и уравнение Дирака нельзя назвать уравнением движения электрона. Определенную ясность тут вносит дополнение, указывающее на то, об уравнении движения чего идет речь: так, хотя уравнение Дирака нельзя назвать уравнением движения электрона, его можно, даже в смысле, обсуждаемом в этом абзаце, назвать классическим уравнением движения спинорного поля.

Примеры

Простой механический пример

Рассмотрим в рамках ньютоновской механики точечную частицу, способную перемещаться лишь по одной прямой (например, бусину, способную скользить по гладкой спице). Будем описывать положение частицы на прямой единственным числом - координатой - x. Пусть на эту частицу действует (например, со стороны некоторой пружины) сила f, зависящая от положения частицы по закону Гука, то есть, выбрав удобное начало отсчета x, можем записать f = - k x. В таком случае, учитывая второй закон Ньютона и кинематические соотношения, обозначив скорость как v, будем иметь следующие уравнения движения для нашей системы:

$~dv/dt = - (k/m) x$

$~dx/dt = v$,

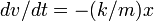
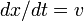или, исключая v из системы:

$~d^2 x/d t^2 = - (k/m) x$

Подставив начальную координату и скорость в правые части этих уравнений, и заменив бесконечно малое dt на малое, но конечное, δt, и переписав приближенно в соответствии с этим уравнения в первой форме - в виде величина(t + δt) = величина(t) + производная·δt, получим:

$~v(t+\delta t) = v(t) - (k/m) x(t) \delta t$

$~x(t+\delta t) = x(t) + v(t) \delta t$,

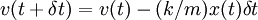
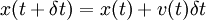и переходя от предыдущего момента к следующему (каждый раз время растет на δt), можем получить численное решение этих уравнений движения в виде таблицы 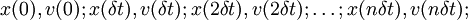${x(0),v(0); x(\delta t),v(\delta t); x(2\delta t),v(2\delta t); \dots; x(n\delta t),v(n\delta t);}$, приближенно представляющей зависимость x(t) и v(t) от времени (с шагом δt). Можно увидеть, что, если δt было выбрано достаточно малым, что x(t) и v(t) очень близко совпадают с функцией $const \cdot \cos(\sqrt{k/m}\cdot t + const')$.

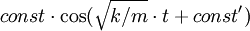Использовав для догадки это приближенное решение или какие-то другие соображения, можем, если мы уже подозреваем, каким должно быть решение, просто подставить

$~x = A \cos(\omega t + \phi)$,

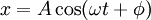где A,ω,φ - просто постоянные, в точные уравнения движения, взяв нужные производные по времени от этого выражения. При этом мы смоожем убедиться, что нетрудно подобрать конкретные значения A,ω,φ, чтобы равенство при этой подстановке выполнялось, а также найти необходимые для этого значения A,ω,φ (оказывается, A и φ могут быть любыми, а 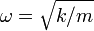$\omega = \sqrt{k/m}$. Мы получили таким образом точное решение уравнений движения, да еще и общее точное решение (то есть подходящее для любых начальных условий, в чём нетрудно убедиться).

Теперь, имея это общее точное решение, мы можем выбрать из множества общих решений (с разными A и φ) частное решение, удовлетворяющее конкретным начальным условиям. Так мы решим задачу для заданного уравнения движения и начальных условий.

Так иллюстрируется понятие уравнения движения (уравнений движения) и их решения на конкретном простом примере.

Примеры уравнений движения в разных областях физики

• В классической механике

Законы Ньютона

(кроме собственно законов Ньютона - а именно второго - в уравнения движения ньютоновской механики входят кинематические уравнения и конкретные законы сил, такие, как например закон всемирного тяготения или закон Гука).

Уравнения Эйлера-Лагранжа

Уравнения Гамильтона

• В классической статистической механике:

Уравнение Лиувилля

Уравнение Боголюбова

Уравнение Больцмана

Уравнение Власова

• В классической теории поля:

Уравнения Максвелла (могут быть записаны и использоваться в разной форме).

• В квантовой механике (см. замечание в основной статье о возможных ограничениях применимости термина уравнения движения в этой области)

Уравнение Шредингера

Уравнение Гейзенберга

Уравнение Линдблада

Уравнение фон Неймана

Уравнение Дирака

Примечания

1. ↑ Когда говорят об уравнениях движения в общеупотребительном смысле, подразумеваются дифференциальные или интегро-дифференциальные уравнения (хотя некоторые другие типы уравнений, например разностные - для дискретных систем - могут представлять собой достаточно близкую аналогию).
2. ↑ Слова "принципе как угодно далеко" означают, что это верно вообще говоря лишь для математической модели (которая всегда лишь с некоторой погрешностью описывает физическую реальность), при этом с абсолютно точно заданными начальными данными; в реальности корректность предсказания состояния системы с помощью уравнений движения на длительный срок вперед определяется погрешностями записи самих уравнений (по сравнению с описываемой ими реальностью), погрешностью задания начальных данных и устойчивостью решений данного конкретного вида уравнений; тем не менее в ряде случаев (хотя и далеко не во всех) на практике предсказание с помощью уравнений движения бывает весьма точным на достаточно больших временных промежутках (как например в небесной механике) или хотя бы удовлетворительным.
3. ↑ Под точным решением, конечно, подразумевается «точное в рамках математической модели», то есть не рассматривая погрешность в написании самих уравнений; могло бы показаться, что получением точных решений незачем заботиться, раз уже и сами уравнения не абсолютно точно отражают физическую реальность, однако, не говоря уж о том, что зачастую погрешность модели достаточно мала и точные в математическом смысле решения, достаточно точны тогда и в физическом, точные решения обладают как правило еще одним преимуществом: они записываются в виде формул в такой форме, которая позволят гораздо удобнее их использовать в дальнейших вычислениях и анализе, что важно и для практики и для теоретического осмысления, ведь одно точное решение с несколькими параметрами представляет собой запись бесконечного семейства единичных решений.