- Начальные условия
-
В теории дифференциальных уравнений, начальные и граничные условия — дополнение к основному дифференциальному уравнению (обыкновенному или в частных производных), задающее его поведение в начальный момент времени или на границе рассматриваемой области соответственно.
Обычно дифференциальное уравнение имеет не одно решение, а целое их семейство. Начальные и граничные условия позволяют выбрать из него одно, соответствующее реальному физическому процессу или явлению. В теории обыкновенных дифференциальных уравнений доказана теорема существования и единственности решения задачи с начальным условием (т. н. задачи Коши). Для уравнений в частных производных получены некоторые теоремы существования и единственности решений для определенных классов начальных и краевых задач.
Содержание
Терминология
Иногда к граничным относят и начальные условия в нестационарных задачах, таких как решение гиперболических или параболических уравнений.
Для стационарных задач существует разделение граничных условий на главные и естественные.
Главные условия обычно имеют вид
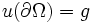 , где
, где 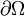 — граница области Ω.
— граница области Ω.Естественные условия содержат также и производную решения по нормали к границе.
Пример
Уравнение
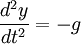 описывает движение тела в поле земного тяготения. Ему удовлетворяет любая квадратичная функция вида y(t) = − gt2 / 2 + at + b, где a,b — произвольные числа. Для выделения конкретного закона движения необходимо указать начальную координату тела и его скорость, то есть начальные условия.
описывает движение тела в поле земного тяготения. Ему удовлетворяет любая квадратичная функция вида y(t) = − gt2 / 2 + at + b, где a,b — произвольные числа. Для выделения конкретного закона движения необходимо указать начальную координату тела и его скорость, то есть начальные условия.Корректность постановки граничных условий
Задачи математической физики описывают реальные физические процессы, а потому их постановка должна удовлетворять следующим естественным требованиям:
- Решение должно существовать в каком-либо классе функций;
- Решение должно быть единственным в каком-либо классе функций;
- Решение должно непрерывно зависеть от данных (начальных и граничных условий, свободного члена, коэффициентов и т.д.).
Требование непрерывной зависимости решения обусловливается тем обстоятельством, что физические данные, как правило, определяются из эксперимента приближенно, и поэтому нужно быть уверенным в том, что решение задачи в рамках выбранной математической модели не будет существенно зависеть от погрешности измерений. Математически это требование можно записать, например, так (для независимости от свободного члена):
Пусть задано два дифференциальных уравнения:
 с одинаковыми дифференциальными операторами и одинаковыми граничными условиями, тогда их решения будут непрерывно зависеть от свободного члена, если:
с одинаковыми дифференциальными операторами и одинаковыми граничными условиями, тогда их решения будут непрерывно зависеть от свободного члена, если:-
 решения соответствующих уравнений.
решения соответствующих уравнений.
Множество функций, для которых выполняются перечисленные требования, называется классом корректности. Некорректную постановку граничных условий хорошо иллюстрирует пример Адамара.
См. также
Литература
Владимиров В.С., Жаринов В.В. Уравнения математической физики. — Физматлит, 2004. — ISBN 5-9221-0310-X
Wikimedia Foundation. 2010.
