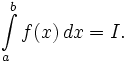Римана интеграл

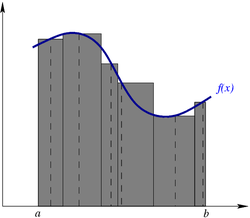Геометрический смысл интеграла Римана

Интегра́л Ри́мана — одно из важнейших понятий математического анализа. Введён Бернхардом Риманом в 1854 году, и является одной из первых формализаций понятия интеграла.

Неформальное геометрическое описание

Риман формализовал понятие интеграла, разработанное Ньютоном и Лейбницем, как площади подграфика (фигуры, заключенной между графиком функции и осью абсцисс). Для этого он рассмотрел фигуры, состоящие из нескольких вертикальных прямоугольников и получающиеся при разбиении отрезка (см. рисунок). Если при «размельчении» разбиения существует предел, к которому сходятся площади таких фигур (интегральные суммы), этот предел называется интегралом Римана функции на отрезке.

Определения

Через интегральные суммы

Пусть на отрезке [a,b] определена вещественнозначная функция f.

Рассмотрим разбиение отрезка 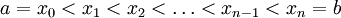$a=x_0 < x_1 < x_2 < \dots < x_{n-1} < x_n=b$ — конечное множество попарно различных точек отрезка. Это разбиение делит отрезок [a,b] на n отрезков $[x_{i-1}, x_{i}],\; i=1\dots n$. Длина наибольшего из отрезков d = max(Δx_i), где Δx_i = x_i − x_{i − 1}, называется диаметром разбиения.

Отметим на каждом отрезке разбиения по точке $\xi _i \in [x_{i-1}, x_i]$. Интегральной суммой называется выражение $\sigma _x = \sum\limits_{i = 1}^n {f(\xi _i )\Delta x_i }$.

Если при стремлении диаметра разбиения к нулю интегральные суммы стремятся к одному и тому же числу, независимо от выбора $\xi _i \in [x_{i-1}, x_i]$, то это число называется интегралом функции f на отрезке [a,b], т.е. $\int\limits_a^b f(x)\,dx = \lim \limits_{d \to 0} \sigma _x$

В этом случае, сама функция f называется интегрируемой (по Риману) на [a,b]; в противном случае f является неинтегрируемой (по Риману) на отрезке [a,b].

Через суммы Дарбу

Суммы Дарбу для разбиения на четыре интервала: нижняя (площадь зелёного) и верхняя (площадь зелёного и серого)

Пусть на отрезке [a,b] определена вещественнозначная функция f. Рассмотрим произвольное разбиение отрезка $\Delta: a=x_0 < x_1 < x_2 < \dots < x_{n-1} < x_n=b$.

Верхней суммой Дарбу Δ называется число

$\overline{S}_{\Delta }=\sum\limits_{i=1}^{n}{\sup _{[x_{i-1},x_{i}]}f(x)\Delta x_{i}}$

Соответственно, нижней суммой Дарбу для Δ называется

$\underline{S}_{\Delta }=\sum\limits_{i=1}^{n}{\inf _{[x_{i-1},x_{i}]} f(x)\Delta x_{i}}$

Функция называется интегрируемой по Риману, если существует вещественное число

$I=\sup_{\Delta} \underline{S}_{\Delta }=\inf_{\Delta} \overline{S}_\Delta$

В этом случае, по определению

$\int\limits_a^b {f(x)\,dx}=I.$

Свойства

• Если функция F является первообразной функции f, то интеграл функции f на отрезке [a,b] может быть вычислен по формуле Ньютона-Лейбница: он равен F(b) − F(a).
• Непрерывная на отрезке функция интегрируема по Риману. Разрывные функции могут быть интегрируемы, но могут и не быть; примером функции, не интегрируемой по Риману, является всюду разрывная функция Дирихле.
• Ограничение: Если функция f интегрируема на отрезке [a,b], то она интегрируема и на меньшем отрезке [a₁,b₁], где $a\le a_1 < b_1\le b$.
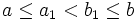• Если функция интегрируема на отрезке [a,b] и на отрезке [b,c], то она интегрируема и на отрезке [a,c], и $\int\limits_a^c f(x)\,dx = \int\limits_a^b f(x)\,dx + \int\limits_b^c f(x)\,dx$.
• Линейность: Если функции f и g интегрируемы, и 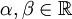$\alpha, \beta \in\R$, то функция αf + βg тоже интегрируема, и

$\int\limits_a^b (\alpha f(x) +\beta g(x))\,dx = \alpha \int\limits_a^b f(x)\,dx + \beta \int\limits_a^b g(x)\,dx$

• Предел: Если интегрируемые функции f_i равномерно сходятся на отрезке [a,b] к функции f, то f интегрируема, и

$\lim_{i\to\infty} \int\limits_a^b f_i(x)\,dx = \int\limits_a^b f(x)\,dx$

История

Такое определение интеграла дано Коши^[1], но применялось только для непрерывных функций.

Риман в 1854 году^[2], дал это же определение без предположения непрерывности.

См. также

• Интеграл Лебега
• Интеграл Даниэля
• Кратный интеграл Римана
• Несобственный интеграл
• Список интегралов

Ссылки

• Таблицы неопределенных и определенных интегралов — EqWorld: Мир математических уравнений.

1. ↑ Cauchy A. L., Sur la mécanique céleste et sur un nouveau calcul appelé calcul des limites, Turin 1831
2. ↑ Riemann В., «Göttinger Akad. Abhandl.», 1868, Bd 13