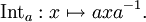Присоединенное представление группы Ли
Полезное
Смотреть что такое "Присоединенное представление группы Ли" в других словарях:
ПРИСОЕДИНЕННОЕ ПРЕДСТАВЛЕНИЕ — группы Ли или алгебраической группы G линейное представление Ad группы Gв касательном пространстве Te(G).(или в алгебре Ли группы G), сопоставляющее каждому дифференциал Ad a=d(Int a)e внутреннего автоморфизма Int a: . Если линейная группа в… … Математическая энциклопедия
Присоединенное представление алгебры Ли — Присоединённое представление алгебры Ли называется линейное представление алгебры в модуле , действующее по формуле где … Википедия
Присоединенное представление лиевой алгебры — Присоединённое представление алгебры Ли называется линейное представление алгебры в модуле , действующее по формуле где … Википедия
Присоединенное представление — Присоединённое представление группы Ли Присоединённое представление алгебры Ли … Википедия
ИНВАРИАНТНАЯ МЕТРИКА — риманова метрика mна многообразии М, не изменяющаяся при всех преобразованиях из данной группы Ли G преобразований. Сама группа G при этом наз. группой движений (изометрий) метрики m(или риманова пространства ( М, т)). Группа Ли G преобразований… … Математическая энциклопедия
ТРЕУГОЛЬНЫЙ ЭЛЕМЕНТ — 1) Т. э. алгебры End V эндоморфизмов конечномерного векторного пространства . над нолем k элемент все собственные значения к рого принадлежат k. Если kалгебраически замкнуто, то всякий элемент из End V треуголен. Для Т. э. X(и только для такого… … Математическая энциклопедия
МАКСИМАЛЬНЫЙ ТОР — 1) М. т. линейной алгебраической группы G алгебраическая подгруппа в G, являющаяся алгебраическим тором и не содержащаяся ни в какой большей подгруппе такого типа. Пусть, далее, группа Gсвязна. Объединение всех М. т. группы Gсовпадает с… … Математическая энциклопедия
ЛИ РЕДУКТИВНАЯ АЛГЕБРА — конечномерная алгебра Ли над полем kхарактеристики 0, присоединенное представление к рой вполне приводимо. Свойство редуктивности алгебры Ли равносильно любому из следующих свойств: 1) радикал алгебры Ли совпадает с центром 2) , где полупростой… … Математическая энциклопедия
ОТНОСИТЕЛЬНАЯ СИСТЕМА КОРНЕЙ — связной редуктивной алгебраической группы G, определенной над полем k, система ненулевых весов присоединенного представления максимального k расщепимого тора Sгруппы G в алгебре Ли g этой группы. Сами веса наз. корнями G относительно S. О. с. к … Математическая энциклопедия
ШЕВАЛЛЕ ГРУППА — линейная алгебраич. группа над нек рым полем, связанная с полупростой комплексной алгеброй Ли. Пусть Ли полупростая алгебра над ее подалгебра Картана, система корней алгебры относительно система простых корней, базис Шевалле алгебры его линейная… … Математическая энциклопедия
 группы G в касательном пространстве TeG (или в алгебре Ли
группы G в касательном пространстве TeG (или в алгебре Ли  группы G), сопоставляющее каждому элементу
группы G), сопоставляющее каждому элементу 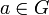 дифференциал
дифференциал — линейная группа в пространстве V, то
— линейная группа в пространстве V, то .
.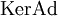 содержит центр группы G.
содержит центр группы G.
 однозначно определяется алгеброй Ли
однозначно определяется алгеброй Ли  и называется иногда присоединённой группой, или группой внутренних автоморфизмов, алгебры Ли
и называется иногда присоединённой группой, или группой внутренних автоморфизмов, алгебры Ли  .
.
 совпадает со связной компонентой единицы в
совпадает со связной компонентой единицы в 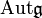 .
.