ШЕВАЛЛЕ ГРУППА

-линейная алгебраич. группа над нек-рым полем, связанная с полупростой комплексной алгеброй Ли. Пусть -Ли полупростая алгебра над -ее подалгебра Картана, -система корней алгебры относительно -система простых корней, -базис Шевалле алгебры - его линейная оболочка над И пусть -точное представление алгебры Ли в конечномерном векторном пространстве V. Оказывается, что в . существует решетка (т. е. свободная абелева подгруппа, базис к-рой является базисом пространства V), инвариантная относительно всех операторов m-натуральное число). Если k- произвольное поле и то определены гомоморфизмы заданные формулами

Подгруппы порождают в GL (V^k) нек-рую подгруппу G_k, к-рая и наз. группой Шевалле, связанной с алгеброй Ли 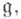представлением полем k. В случае, когда (присоединенное представление), Ш. г. были определены К. Шевалле (С. Chevalley) в 1955 (см. [1]).
Если К - алгебраически замкнутое поле, содержащее k, то Ш. г. С _K есть связная полупростая линейная алгебраич. группа над К. определенная и разложимая над простым подполем Ее алгебра Ли изоморфна 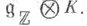Группа G_k является коммутантом группы G_K(k) точек группы G_K, рациональных над k. Любая связная полупростая линейная алгебраич. группа над K изоморфна одной из Ш. г. Алгебраич. группы G_K (и G_k как абстрактные группы) зависят лишь от решетки порожденной весами представления Если Г _j совпадает с решеткой корней Г ₀, то G_K наз. присоединенной группой, а еели =Г ₁ (решетка весов, см. Ли полупростая группа), то G_K наз. универсальной, или односвяаной, группой. Если G_K- универсальна, то G_k = G_K(k).
Ш. г. G_K всегда совпадает со своим коммутантом. Центр группы G_k конечен. Напр., центр Zуниверсальной группы G_k изоморфен Ноm (Г ₁/Г ₀, k^*), а соответствующая присоединенная группа изоморфна G_k/Z и имеет тривиальный центр.
Если алгебра проста, то присоединенная Ш. г. G_k проста, за исключением следующих случаев: |k| =2, - алгебра Ли типов A₁, B₂, G₂; |k|=3, 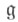-алгебра Ли типа А ₁. Другие серии простых групп можно получить, рассматривая подгруппы неподвижных точек нек-рых автоморфизмов конечного порядка Ш. г. (т. н. скрученные группы).
Если поле k конечно, то порядок универсальной группы G_k вычисляется по формуле

где q = |k|, d_i(i = l, . .., r) - показатели алгебры Ли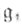 т. е. степени свободных образующих алгебры многочленов на 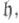инвариантных относительно Вейля группы, 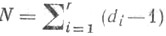- число положительных корней.
Имеется развитая теория рациональных линейных представлений Ш. г. G_k над бесконечным полем k, сводящаяся к случаю алгебраически замкнутого поля, а в последнем случае совпадающая с теорией рациональных представлений полупростых алгебраич. групп. Если проста, G_k- универсальная Ш. г. над бесконечным полем . и -нетривиальное неприводимое конечномерное представление группы G_k (как абстрактной группы) над алгебраически замкнутым полем K, то, существуют такой конечный набор вложений и такой набор рациональных представлений групп что По поводу представлений Ш. г. см. также [2], [3], [5].

Лит.:[1] Шевалле К., лМатематика