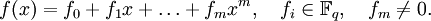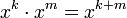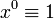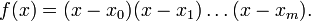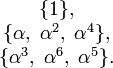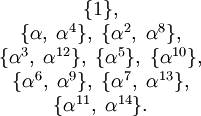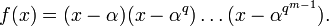Полином над конечным полем

Многочленом f(x) над конечным полем 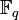$\Bbb{F}_q$ степени 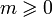$m\geqslant 0$ называется формальная сумма следующего вида

$f(x)=f_0+f_1 x+\ldots+f_m x^m,\quad f_i\in \Bbb{F}_q,\quad f_m\neq 0.$

Здесь x^k — элементы алгебры над 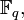$\Bbb{F}_q,$ умножение которых задаётся по правилу

$x^k \cdot x^m = x^{k+m}$

$x^0 \equiv 1$

Такое определение позволяет умножать многочлены формально, не заботясь о том, что разные степени одного и того элемента конечного поля могут совпадать.

Основные определения и понятия

• Число 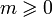$m\geqslant 0$ называется степенью полинома и обозначается как deg(f(x)).
• Если f_m = 1, то полином называется нормированным или унитарным.
• Сумма и произведение полиномов определены обычном образом, а операции с коэффициентами происходят как операции в поле $\Bbb{F}_q$.
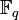• Для двух полиномов f(x) и h(x) таких, что 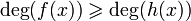$\deg(f(x))\geqslant\deg(h(x))$, всегда найдутся полиномы t(x) и r(x) над полем 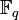$\Bbb{F}_q$, что будет выполнятся соотношение

f(x) = t(x)h(x) + r(x).

Если степень r(x) строго меньше степени h(x), то такое соотношение называется представлением полинома f(x) в виде частного и остатка от деления f(x) на h(x). Причем, такое представление единственно. Ясно, что f(x) − r(x) делится без остатка на h(x), что записывается как $f(x)=r(x)\,\bmod\,h(x)$.

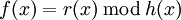• Полином h(x) является сомножителем (или делителем) полинома f(x), если остаток от деления r(x) равен нулю. Ясно, что полином можно разделить на любой ненулевой скаляр из поля 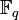$\Bbb{F}_q$. Поэтому любой полином можно нормировать делением его на коэффициент f_m при старшей степени.
• Полином является неприводимым над полем 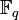$\Bbb{F}_q$, если он среди своих делителей не имеет других полиномов.

Корни полинома

Корнем называется такой некоторый элемент, что подставленный вместо переменной x, обращает полином в ноль. Полином степени m имеет ровно m корней, принадлежащих некоторому расширеному полю 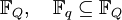$\Bbb{F}_Q,\quad \Bbb{F}_q\subseteq \Bbb{F}_Q$. Если q = p^s, где p — простое, то 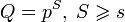$Q=p^S,\;S\geqslant s$. Исходя из свойств конечных полей, любой элемент поля 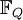$\Bbb{F}_Q$ является корнем двучлена x^Q − x. таким образом, корни полинома f(x) лежат среди корней двучлена x^Q − x.

Справедливы теорема Безу и следствия к ней.

Остаток от деления f(x) на (x − a) равен f(a).

Если x0 — корень f(x), то (x − x0) делит f(x) без остатка.

Если 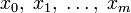$x_0,\;x_1,\;\ldots,\;x_m$ суть корни f(x), то $f(x) = (x-x_0)(x-x_1)\ldots(x-x_m).$

Также справедлива следующая Теорема 1:

Если x0 — корень f(x), то 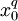$x_0^q$ — тоже корень f(x).

Циклотомический класс

Следствием Теоремы 1 может быть тот факт, что, если 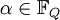$\alpha\in \Bbb{F}_Q$ — корень полинома f(x) над полем 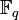$\Bbb{F}_q$, то и 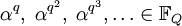$\alpha^q,\;\alpha^{q^2},\;\alpha^{q^3},\ldots\in \Bbb{F}_Q$ являются его корнями.

Определение: циклотомическим классом над полем 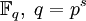$\Bbb{F}_q,\;q=p^s$, порождённым некоторым элементом 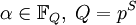$\alpha\in \Bbb{F}_Q,\;Q=p^S$ называется множество всех различных элементов 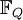$\Bbb{F}_Q$, являющихся q-ыми степенями α.

Если α — примитивный элемент (такой элемент, что α^{Q − 1} = 1 и 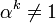$\alpha^k\neq 1$ при 0 < k < Q − 1) поля 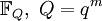$\Bbb{F}_Q,\;Q=q^m$, то циклотомический класс 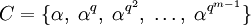$C=\{\alpha,\;\alpha^q,\;\alpha^{q^2},\;\ldots,\;\alpha^{q^{m-1}}\}$ над полем 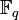$\Bbb{F}_q$ будет иметь ровно m элементов.

Следует отметить, что любой элемент из циклотомического класса может порождать этот и только этот класс, а, следовательно, и принадлежать только ему.

Примеры циклотомических классов

Пример 1 Пусть q = 2, Q = 2³ = 8 и α — примитивный элемент поля 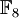$\Bbb{F}_8$, то есть α⁷ = 1 и 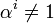$\alpha^i\neq 1$ при i < 7. Учитывая также, что α⁸ = α, можно получить разложение всех ненулевых элементов поля 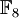$\Bbb{F}_8$ на три циклотомических класса над полем $\Bbb{F}_2$:

$\begin{matrix} \{1\}, \\ \{\alpha,\;\alpha^2,\;\alpha^4\}, \\ \{\alpha^3,\;\alpha^6,\;\alpha^5\}. \end{matrix}$

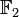Пример 2 Аналогично можно построить классы на поле 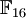$\Bbb{F}_{16}$ над полем 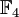$\Bbb{F}_4$, то есть 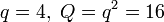$q=4,\;Q=q^2=16$. Пусть α — примитивный элемент поля 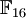$\Bbb{F}_{16}$, значит $\alpha^{15}=1,\;\alpha^{16}=\alpha$.

$\begin{matrix} \{1\}, \\ \{\alpha,\;\alpha^4\},\;\{\alpha^2,\;\alpha^8\}, \\ \{\alpha^3,\;\alpha^{12}\},\;\{\alpha^5\},\;\{\alpha^{10}\}, \\ \{\alpha^6,\;\alpha^9\},\;\{\alpha^7,\;\alpha^{13}\}, \\ \{\alpha^{11},\;\alpha^{14}\}. \end{matrix}$

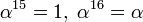Связь с корнями полиномов

Следующая Теорема устанавливает связь между циклотомическими классами и разложением полинома x^{Q − 1} − 1 на неприводимые полиномы над полем $\Bbb{F}_q$.

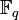Теорема 2. Пусть 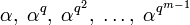$\alpha,\;\alpha^q,\;\alpha^{q^2},\;\ldots,\;\alpha^{q^{m-1}}$ циклотомический класс, порожденный элементом 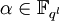$\alpha\in \Bbb{F}_{q^l}$ и полином 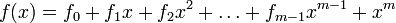$f(x)=f_0+f_1 x+f_2 x^2+\ldots+f_{m-1}x^{m-1}+x^m$ имеет в качестве своих корней элементы этого циклотомического класса, то есть $f(x)=(x-\alpha)(x-\alpha^q)\ldots(x-\alpha^{q^{m-1}}).$ Тогда коэффициенты 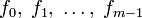$f_0,\;f_1,\;\ldots,\;f_{m-1}$ полинома f(x) лежат в поле 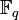$\Bbb{F}_q$, а сам полином является неприводимым над этим полем.

Можно установить такое следствие из Теоремы 2. Из свойства конечных полей, говорящего о том, что все ненулевые элементы поля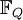 $\Bbb{F}_Q$ являются корнями многочлена x^{Q − 1} − 1, можно заключить, что многочлен x^{Q − 1} − 1 можно разложить на неприводимые над полем 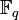$\Bbb{F}_q$ многочлены 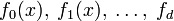$f_0(x),\;f_1(x),\;\ldots,\;f_d$, каждый из которых соответсвует своему циклотомичесому классу.

См. также

• Конечное поле