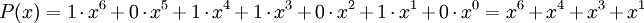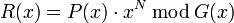- Циклическая проверка на четность
-
Алгоритм вычисления контрольной суммы (англ. Cyclic redundancy code, CRC — циклический избыточный код) — способ цифровой идентификации некоторой последовательности данных, который заключается в вычислении контрольного значения её циклического избыточного кода.
Содержание
Алгоритм CRC
Алгоритм CRC базируется на свойствах деления с остатком двоичных многочленов, то есть многочленов над конечным полем GF(2). Значение CRC является по сути остатком от деления многочлена, соответствующего входным данным, на некий фиксированный порождающий многочлен (полином).
Каждой конечной последовательности битов
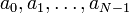 взаимооднозначно сопоставляется двоичный многочлен
взаимооднозначно сопоставляется двоичный многочлен 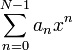 , последовательность коэффициентов которого представляет собой исходную последовательность. Например, последовательность битов 0,1,0,1,1,0,1 соответствует многочлену:
, последовательность коэффициентов которого представляет собой исходную последовательность. Например, последовательность битов 0,1,0,1,1,0,1 соответствует многочлену:Нетрудно видеть, что количество различных многочленов степени меньшей N равно 2N, что совпадает с числом всех двоичных последовательностей длины N.
Значение CRC с порождающим многочленом G(x) степени N определяется как битовая последовательность длины N, представляющая многочлен R(x), получившийся в остатке при делении многочлена P(x), представляющего входной поток бит, на многочлен G(x):
где
- R(x) — многочлен, представляющий значение CRC.
- P(x) — многочлен, коэффициенты которого представляют входные данные.
- G(x) — порождающий многочлен.
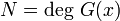 — степень порождающего многочлена.
— степень порождающего многочлена.
Умножение xN осуществляется приписыванием N нулевых битов к входной последовательности, что улучшает качество хеширования для коротких входных последовательностей.
При делении с остатком степень многочлена-остатка строго меньше степени многочлена-делителя, то есть при делении на многочлен G(x) степени N можно получить 2N различных остатков от деления. При «правильном» выборе порождающего многочлена G(x), остатки от деления на него будут обладать нужными свойствами хеширования — хорошей перемешиваемостью и быстрым алгоритмом вычисления. Второе обеспечивается тем, что степень порождающего многочлена обычно пропорциональна длине байта или машинного слова (например 8, 16 или 32).
Операция деления на примитивный полином также эквивалентна следующей схеме: Пусть выбран примитивный полином, задающий цикл де Брейна 0010111001011100… и блок данных 0111110, построена таблица, верхняя строка заполнена блоком данных, а нижние строки — смещения на 0,1,2 бит цикла де Брейна
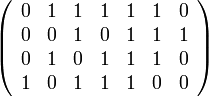
Тогда контрольная сумма будет равна операции XOR тех столбцов, над которыми в верхней строке расположена 1. В этом случае, 010 xor 101 xor 011 xor 111 xor 110 = 101 (CRC).
Ниже представлены реализации получения некоторых CRC для многочленов степени 8 (CRC-8), 16 (CRC-16) и 32 (CRC-32).Формализованный алгоритм расчёта CRC16
Для получения контрольной суммы, необходимо сгенерировать полином. Основное требование к полиному: его степень должна быть равна длине контрольной суммы в битах. При этом старший бит полинома обязательно должен быть равен «1».
Из файла берется первое слово. В зависимости от того, равен ли старший бит этого слова «1» или нет, выполняем (или нет) операцию XOR на полином. Полученный результат, вне зависимости от того, выполнялась ли операция XOR, сдвигаем на один бит влево (то есть умножаем на 2). После сдвига (умножения) теряется старый старший бит, а младший бит освобождается (обнуляется). На место младшего бита загружается очередной бит из файла. Операция повторяется до тех пор, пока не загрузится последний бит файла.
После прохождения всего файла, в слове остается остаток, который и является контрольной суммой.
CRC-8
Пример программы расчёта CRC8 на языке Си/* Name : CRC-8 Poly : 0x31 x^8 + x^5 + x^4 + 1 Init : 0xFF Revert: false XorOut: 0x00 Check : 0xF7 ("123456789") MaxLen: 15 байт(127 бит) - обнаружение одинарных, двойных, тройных и всех нечетных ошибок */ unsigned char Crc8(unsigned char *pcBlock, unsigned char len) { unsigned char crc = 0xFF; unsigned char i; while (len--) { crc ^= *pcBlock++; for (i = 0; i < 8; i++) crc = crc & 0x80 ? (crc << 1) ^ 0x31 : crc << 1; } return crc; }
Пример программы табличного (быстрого) расчёта CRC8 на языке Си/* Name : CRC-8 Poly : 0x31 x^8 + x^5 + x^4 + 1 Init : 0xFF Revert: false XorOut: 0x00 Check : 0xF7 ("123456789") MaxLen: 15 байт (127 бит) - обнаружение одинарных, двойных, тройных и всех нечетных ошибок */ const unsigned char Crc8Table[256] = { 0x00, 0x31, 0x62, 0x53, 0xC4, 0xF5, 0xA6, 0x97, 0xB9, 0x88, 0xDB, 0xEA, 0x7D, 0x4C, 0x1F, 0x2E, 0x43, 0x72, 0x21, 0x10, 0x87, 0xB6, 0xE5, 0xD4, 0xFA, 0xCB, 0x98, 0xA9, 0x3E, 0x0F, 0x5C, 0x6D, 0x86, 0xB7, 0xE4, 0xD5, 0x42, 0x73, 0x20, 0x11, 0x3F, 0x0E, 0x5D, 0x6C, 0xFB, 0xCA, 0x99, 0xA8, 0xC5, 0xF4, 0xA7, 0x96, 0x01, 0x30, 0x63, 0x52, 0x7C, 0x4D, 0x1E, 0x2F, 0xB8, 0x89, 0xDA, 0xEB, 0x3D, 0x0C, 0x5F, 0x6E, 0xF9, 0xC8, 0x9B, 0xAA, 0x84, 0xB5, 0xE6, 0xD7, 0x40, 0x71, 0x22, 0x13, 0x7E, 0x4F, 0x1C, 0x2D, 0xBA, 0x8B, 0xD8, 0xE9, 0xC7, 0xF6, 0xA5, 0x94, 0x03, 0x32, 0x61, 0x50, 0xBB, 0x8A, 0xD9, 0xE8, 0x7F, 0x4E, 0x1D, 0x2C, 0x02, 0x33, 0x60, 0x51, 0xC6, 0xF7, 0xA4, 0x95, 0xF8, 0xC9, 0x9A, 0xAB, 0x3C, 0x0D, 0x5E, 0x6F, 0x41, 0x70, 0x23, 0x12, 0x85, 0xB4, 0xE7, 0xD6, 0x7A, 0x4B, 0x18, 0x29, 0xBE, 0x8F, 0xDC, 0xED, 0xC3, 0xF2, 0xA1, 0x90, 0x07, 0x36, 0x65, 0x54, 0x39, 0x08, 0x5B, 0x6A, 0xFD, 0xCC, 0x9F, 0xAE, 0x80, 0xB1, 0xE2, 0xD3, 0x44, 0x75, 0x26, 0x17, 0xFC, 0xCD, 0x9E, 0xAF, 0x38, 0x09, 0x5A, 0x6B, 0x45, 0x74, 0x27, 0x16, 0x81, 0xB0, 0xE3, 0xD2, 0xBF, 0x8E, 0xDD, 0xEC, 0x7B, 0x4A, 0x19, 0x28, 0x06, 0x37, 0x64, 0x55, 0xC2, 0xF3, 0xA0, 0x91, 0x47, 0x76, 0x25, 0x14, 0x83, 0xB2, 0xE1, 0xD0, 0xFE, 0xCF, 0x9C, 0xAD, 0x3A, 0x0B, 0x58, 0x69, 0x04, 0x35, 0x66, 0x57, 0xC0, 0xF1, 0xA2, 0x93, 0xBD, 0x8C, 0xDF, 0xEE, 0x79, 0x48, 0x1B, 0x2A, 0xC1, 0xF0, 0xA3, 0x92, 0x05, 0x34, 0x67, 0x56, 0x78, 0x49, 0x1A, 0x2B, 0xBC, 0x8D, 0xDE, 0xEF, 0x82, 0xB3, 0xE0, 0xD1, 0x46, 0x77, 0x24, 0x15, 0x3B, 0x0A, 0x59, 0x68, 0xFF, 0xCE, 0x9D, 0xAC }; unsigned char Crc8(unsigned char *pcBlock, unsigned char len) { unsigned char crc = 0xFF; while (len--) crc = Crc8Table[crc ^ *pcBlock++]; return crc; }
CRC-16
CRC-CCITT (отличается от классического CRC-16, так как использует другой полином и порядок данных).
Пример программы расчёта CRC-16 CCITT на языке Си/* Name : CRC-16 CCITT Poly : 0x1021 x^16 + x^12 + x^5 + 1 Init : 0xFFFF Revert: false XorOut: 0x0000 Check : 0x29B1 ("123456789") MaxLen: 4095 байт (32767 бит) - обнаружение одинарных, двойных, тройных и всех нечетных ошибок */ unsigned short Crc16( unsigned char *pcBlock, unsigned short len ) { unsigned short crc = 0xFFFF; unsigned char i; while( len-- ) { crc ^= *pcBlock++ << 8; for( i = 0; i < 8; i++ ) crc = crc & 0x8000 ? ( crc << 1 ) ^ 0x1021 : crc << 1; } return crc; }
Пример программы табличного (быстрого) расчёта CRC-16 CCITT на языке Си/* Name : CRC-16 CCITT Poly : 0x1021 x^16 + x^12 + x^5 + 1 Init : 0xFFFF Revert: false XorOut: 0x0000 Check : 0x29B1 ("123456789") MaxLen: 4095 байт (32767 бит) - обнаружение одинарных, двойных, тройных и всех нечетных ошибок */ const unsigned short Crc16Table[256] = { 0x0000, 0x1021, 0x2042, 0x3063, 0x4084, 0x50A5, 0x60C6, 0x70E7, 0x8108, 0x9129, 0xA14A, 0xB16B, 0xC18C, 0xD1AD, 0xE1CE, 0xF1EF, 0x1231, 0x0210, 0x3273, 0x2252, 0x52B5, 0x4294, 0x72F7, 0x62D6, 0x9339, 0x8318, 0xB37B, 0xA35A, 0xD3BD, 0xC39C, 0xF3FF, 0xE3DE, 0x2462, 0x3443, 0x0420, 0x1401, 0x64E6, 0x74C7, 0x44A4, 0x5485, 0xA56A, 0xB54B, 0x8528, 0x9509, 0xE5EE, 0xF5CF, 0xC5AC, 0xD58D, 0x3653, 0x2672, 0x1611, 0x0630, 0x76D7, 0x66F6, 0x5695, 0x46B4, 0xB75B, 0xA77A, 0x9719, 0x8738, 0xF7DF, 0xE7FE, 0xD79D, 0xC7BC, 0x48C4, 0x58E5, 0x6886, 0x78A7, 0x0840, 0x1861, 0x2802, 0x3823, 0xC9CC, 0xD9ED, 0xE98E, 0xF9AF, 0x8948, 0x9969, 0xA90A, 0xB92B, 0x5AF5, 0x4AD4, 0x7AB7, 0x6A96, 0x1A71, 0x0A50, 0x3A33, 0x2A12, 0xDBFD, 0xCBDC, 0xFBBF, 0xEB9E, 0x9B79, 0x8B58, 0xBB3B, 0xAB1A, 0x6CA6, 0x7C87, 0x4CE4, 0x5CC5, 0x2C22, 0x3C03, 0x0C60, 0x1C41, 0xEDAE, 0xFD8F, 0xCDEC, 0xDDCD, 0xAD2A, 0xBD0B, 0x8D68, 0x9D49, 0x7E97, 0x6EB6, 0x5ED5, 0x4EF4, 0x3E13, 0x2E32, 0x1E51, 0x0E70, 0xFF9F, 0xEFBE, 0xDFDD, 0xCFFC, 0xBF1B, 0xAF3A, 0x9F59, 0x8F78, 0x9188, 0x81A9, 0xB1CA, 0xA1EB, 0xD10C, 0xC12D, 0xF14E, 0xE16F, 0x1080, 0x00A1, 0x30C2, 0x20E3, 0x5004, 0x4025, 0x7046, 0x6067, 0x83B9, 0x9398, 0xA3FB, 0xB3DA, 0xC33D, 0xD31C, 0xE37F, 0xF35E, 0x02B1, 0x1290, 0x22F3, 0x32D2, 0x4235, 0x5214, 0x6277, 0x7256, 0xB5EA, 0xA5CB, 0x95A8, 0x8589, 0xF56E, 0xE54F, 0xD52C, 0xC50D, 0x34E2, 0x24C3, 0x14A0, 0x0481, 0x7466, 0x6447, 0x5424, 0x4405, 0xA7DB, 0xB7FA, 0x8799, 0x97B8, 0xE75F, 0xF77E, 0xC71D, 0xD73C, 0x26D3, 0x36F2, 0x0691, 0x16B0, 0x6657, 0x7676, 0x4615, 0x5634, 0xD94C, 0xC96D, 0xF90E, 0xE92F, 0x99C8, 0x89E9, 0xB98A, 0xA9AB, 0x5844, 0x4865, 0x7806, 0x6827, 0x18C0, 0x08E1, 0x3882, 0x28A3, 0xCB7D, 0xDB5C, 0xEB3F, 0xFB1E, 0x8BF9, 0x9BD8, 0xABBB, 0xBB9A, 0x4A75, 0x5A54, 0x6A37, 0x7A16, 0x0AF1, 0x1AD0, 0x2AB3, 0x3A92, 0xFD2E, 0xED0F, 0xDD6C, 0xCD4D, 0xBDAA, 0xAD8B, 0x9DE8, 0x8DC9, 0x7C26, 0x6C07, 0x5C64, 0x4C45, 0x3CA2, 0x2C83, 0x1CE0, 0x0CC1, 0xEF1F, 0xFF3E, 0xCF5D, 0xDF7C, 0xAF9B, 0xBFBA, 0x8FD9, 0x9FF8, 0x6E17, 0x7E36, 0x4E55, 0x5E74, 0x2E93, 0x3EB2, 0x0ED1, 0x1EF0 }; unsigned short Crc16(unsigned char * pcBlock, unsigned short len) { unsigned short crc = 0xFFFF; while (len--) crc = (crc << 8) ^ Crc16Table[(crc >> 8) ^ *pcBlock++]; return crc; }
Пример программы табличного (быстрого) расчёта стандартного (ARC) CRC-16 на языке Си/* Name : CRC-16 Poly : 0x8005 x^16 + x^15 + x^2 + 1 Init : 0x0000 Revert: true XorOut: 0x0000 Check : 0x4B37 ("123456789") MaxLen: 4095 байт (32767 бит) - обнаружение одинарных, двойных, тройных и всех нечетных ошибок */ const unsigned short Crc16Table[256] = { 0x0000, 0xC0C1, 0xC181, 0x0140, 0xC301, 0x03C0, 0x0280, 0xC241, 0xC601, 0x06C0, 0x0780, 0xC741, 0x0500, 0xC5C1, 0xC481, 0x0440, 0xCC01, 0x0CC0, 0x0D80, 0xCD41, 0x0F00, 0xCFC1, 0xCE81, 0x0E40, 0x0A00, 0xCAC1, 0xCB81, 0x0B40, 0xC901, 0x09C0, 0x0880, 0xC841, 0xD801, 0x18C0, 0x1980, 0xD941, 0x1B00, 0xDBC1, 0xDA81, 0x1A40, 0x1E00, 0xDEC1, 0xDF81, 0x1F40, 0xDD01, 0x1DC0, 0x1C80, 0xDC41, 0x1400, 0xD4C1, 0xD581, 0x1540, 0xD701, 0x17C0, 0x1680, 0xD641, 0xD201, 0x12C0, 0x1380, 0xD341, 0x1100, 0xD1C1, 0xD081, 0x1040, 0xF001, 0x30C0, 0x3180, 0xF141, 0x3300, 0xF3C1, 0xF281, 0x3240, 0x3600, 0xF6C1, 0xF781, 0x3740, 0xF501, 0x35C0, 0x3480, 0xF441, 0x3C00, 0xFCC1, 0xFD81, 0x3D40, 0xFF01, 0x3FC0, 0x3E80, 0xFE41, 0xFA01, 0x3AC0, 0x3B80, 0xFB41, 0x3900, 0xF9C1, 0xF881, 0x3840, 0x2800, 0xE8C1, 0xE981, 0x2940, 0xEB01, 0x2BC0, 0x2A80, 0xEA41, 0xEE01, 0x2EC0, 0x2F80, 0xEF41, 0x2D00, 0xEDC1, 0xEC81, 0x2C40, 0xE401, 0x24C0, 0x2580, 0xE541, 0x2700, 0xE7C1, 0xE681, 0x2640, 0x2200, 0xE2C1, 0xE381, 0x2340, 0xE101, 0x21C0, 0x2080, 0xE041, 0xA001, 0x60C0, 0x6180, 0xA141, 0x6300, 0xA3C1, 0xA281, 0x6240, 0x6600, 0xA6C1, 0xA781, 0x6740, 0xA501, 0x65C0, 0x6480, 0xA441, 0x6C00, 0xACC1, 0xAD81, 0x6D40, 0xAF01, 0x6FC0, 0x6E80, 0xAE41, 0xAA01, 0x6AC0, 0x6B80, 0xAB41, 0x6900, 0xA9C1, 0xA881, 0x6840, 0x7800, 0xB8C1, 0xB981, 0x7940, 0xBB01, 0x7BC0, 0x7A80, 0xBA41, 0xBE01, 0x7EC0, 0x7F80, 0xBF41, 0x7D00, 0xBDC1, 0xBC81, 0x7C40, 0xB401, 0x74C0, 0x7580, 0xB541, 0x7700, 0xB7C1, 0xB681, 0x7640, 0x7200, 0xB2C1, 0xB381, 0x7340, 0xB101, 0x71C0, 0x7080, 0xB041, 0x5000, 0x90C1, 0x9181, 0x5140, 0x9301, 0x53C0, 0x5280, 0x9241, 0x9601, 0x56C0, 0x5780, 0x9741, 0x5500, 0x95C1, 0x9481, 0x5440, 0x9C01, 0x5CC0, 0x5D80, 0x9D41, 0x5F00, 0x9FC1, 0x9E81, 0x5E40, 0x5A00, 0x9AC1, 0x9B81, 0x5B40, 0x9901, 0x59C0, 0x5880, 0x9841, 0x8801, 0x48C0, 0x4980, 0x8941, 0x4B00, 0x8BC1, 0x8A81, 0x4A40, 0x4E00, 0x8EC1, 0x8F81, 0x4F40, 0x8D01, 0x4DC0, 0x4C80, 0x8C41, 0x4400, 0x84C1, 0x8581, 0x4540, 0x8701, 0x47C0, 0x4680, 0x8641, 0x8201, 0x42C0, 0x4380, 0x8341, 0x4100, 0x81C1, 0x8081, 0x4040 }; unsigned short Crc16(unsigned char * pcBlock, unsigned short len) { unsigned short crc = 0; while (len--) crc = (crc >> 8) ^ Crc16Table[(crc & 0xFF) ^ *pcBlock++]; return crc; }
CRC-32
Алгоритм CRC32 основан на примитивном полиноме 0xEDB88320 (зеркальное отображение полинома 0x04C11DB7).
Пример программы расчёта CRC32 на языке Си/* Name : CRC-32 Poly : 0x04C11DB7 x^32 + x^26 + x^23 + x^22 + x^16 + x^12 + x^11 + x^10 + x^8 + x^7 + x^5 + x^4 + x^2 + x + 1 Init : 0xFFFFFFFF Revert: true XorOut: 0xFFFFFFFF Check : 0xCBF43926 ("123456789") MaxLen: 268 435 455 байт (2 147 483 647 бит) - обнаружение одинарных, двойных, пакетных и всех нечетных ошибок */ unsigned long Crc32(unsigned char *buf, unsigned long len) { unsigned long crc_table[256]; unsigned long crc; for (int i = 0; i < 256; i++) { crc = i; for (int j = 0; j < 8; j++) crc = crc & 1 ? (crc >> 1) ^ 0xEDB88320UL : crc >> 1; crc_table[i] = crc; }; crc = 0xFFFFFFFFUL; while (len--) crc = crc_table[(crc ^ *buf++) & 0xFF] ^ (crc >> 8); return crc ^ 0xFFFFFFFFUL; }
Пример программы табличного (быстрого) расчёта CRC-32 на языке Си/* Name : CRC-32 Poly : 0x04C11DB7 x^32 + x^26 + x^23 + x^22 + x^16 + x^12 + x^11 + x^10 + x^8 + x^7 + x^5 + x^4 + x^2 + x + 1 Init : 0xFFFFFFFF Revert: true XorOut: 0xFFFFFFFF Check : 0xCBF43926 ("123456789") MaxLen: 268 435 455 байт (2 147 483 647 бит) - обнаружение одинарных, двойных, пакетных и всех нечетных ошибок */ const unsigned int Crc32Table[256] = { 0x00000000, 0x77073096, 0xEE0E612C, 0x990951BA, 0x076DC419, 0x706AF48F, 0xE963A535, 0x9E6495A3, 0x0EDB8832, 0x79DCB8A4, 0xE0D5E91E, 0x97D2D988, 0x09B64C2B, 0x7EB17CBD, 0xE7B82D07, 0x90BF1D91, 0x1DB71064, 0x6AB020F2, 0xF3B97148, 0x84BE41DE, 0x1ADAD47D, 0x6DDDE4EB, 0xF4D4B551, 0x83D385C7, 0x136C9856, 0x646BA8C0, 0xFD62F97A, 0x8A65C9EC, 0x14015C4F, 0x63066CD9, 0xFA0F3D63, 0x8D080DF5, 0x3B6E20C8, 0x4C69105E, 0xD56041E4, 0xA2677172, 0x3C03E4D1, 0x4B04D447, 0xD20D85FD, 0xA50AB56B, 0x35B5A8FA, 0x42B2986C, 0xDBBBC9D6, 0xACBCF940, 0x32D86CE3, 0x45DF5C75, 0xDCD60DCF, 0xABD13D59, 0x26D930AC, 0x51DE003A, 0xC8D75180, 0xBFD06116, 0x21B4F4B5, 0x56B3C423, 0xCFBA9599, 0xB8BDA50F, 0x2802B89E, 0x5F058808, 0xC60CD9B2, 0xB10BE924, 0x2F6F7C87, 0x58684C11, 0xC1611DAB, 0xB6662D3D, 0x76DC4190, 0x01DB7106, 0x98D220BC, 0xEFD5102A, 0x71B18589, 0x06B6B51F, 0x9FBFE4A5, 0xE8B8D433, 0x7807C9A2, 0x0F00F934, 0x9609A88E, 0xE10E9818, 0x7F6A0DBB, 0x086D3D2D, 0x91646C97, 0xE6635C01, 0x6B6B51F4, 0x1C6C6162, 0x856530D8, 0xF262004E, 0x6C0695ED, 0x1B01A57B, 0x8208F4C1, 0xF50FC457, 0x65B0D9C6, 0x12B7E950, 0x8BBEB8EA, 0xFCB9887C, 0x62DD1DDF, 0x15DA2D49, 0x8CD37CF3, 0xFBD44C65, 0x4DB26158, 0x3AB551CE, 0xA3BC0074, 0xD4BB30E2, 0x4ADFA541, 0x3DD895D7, 0xA4D1C46D, 0xD3D6F4FB, 0x4369E96A, 0x346ED9FC, 0xAD678846, 0xDA60B8D0, 0x44042D73, 0x33031DE5, 0xAA0A4C5F, 0xDD0D7CC9, 0x5005713C, 0x270241AA, 0xBE0B1010, 0xC90C2086, 0x5768B525, 0x206F85B3, 0xB966D409, 0xCE61E49F, 0x5EDEF90E, 0x29D9C998, 0xB0D09822, 0xC7D7A8B4, 0x59B33D17, 0x2EB40D81, 0xB7BD5C3B, 0xC0BA6CAD, 0xEDB88320, 0x9ABFB3B6, 0x03B6E20C, 0x74B1D29A, 0xEAD54739, 0x9DD277AF, 0x04DB2615, 0x73DC1683, 0xE3630B12, 0x94643B84, 0x0D6D6A3E, 0x7A6A5AA8, 0xE40ECF0B, 0x9309FF9D, 0x0A00AE27, 0x7D079EB1, 0xF00F9344, 0x8708A3D2, 0x1E01F268, 0x6906C2FE, 0xF762575D, 0x806567CB, 0x196C3671, 0x6E6B06E7, 0xFED41B76, 0x89D32BE0, 0x10DA7A5A, 0x67DD4ACC, 0xF9B9DF6F, 0x8EBEEFF9, 0x17B7BE43, 0x60B08ED5, 0xD6D6A3E8, 0xA1D1937E, 0x38D8C2C4, 0x4FDFF252, 0xD1BB67F1, 0xA6BC5767, 0x3FB506DD, 0x48B2364B, 0xD80D2BDA, 0xAF0A1B4C, 0x36034AF6, 0x41047A60, 0xDF60EFC3, 0xA867DF55, 0x316E8EEF, 0x4669BE79, 0xCB61B38C, 0xBC66831A, 0x256FD2A0, 0x5268E236, 0xCC0C7795, 0xBB0B4703, 0x220216B9, 0x5505262F, 0xC5BA3BBE, 0xB2BD0B28, 0x2BB45A92, 0x5CB36A04, 0xC2D7FFA7, 0xB5D0CF31, 0x2CD99E8B, 0x5BDEAE1D, 0x9B64C2B0, 0xEC63F226, 0x756AA39C, 0x026D930A, 0x9C0906A9, 0xEB0E363F, 0x72076785, 0x05005713, 0x95BF4A82, 0xE2B87A14, 0x7BB12BAE, 0x0CB61B38, 0x92D28E9B, 0xE5D5BE0D, 0x7CDCEFB7, 0x0BDBDF21, 0x86D3D2D4, 0xF1D4E242, 0x68DDB3F8, 0x1FDA836E, 0x81BE16CD, 0xF6B9265B, 0x6FB077E1, 0x18B74777, 0x88085AE6, 0xFF0F6A70, 0x66063BCA, 0x11010B5C, 0x8F659EFF, 0xF862AE69, 0x616BFFD3, 0x166CCF45, 0xA00AE278, 0xD70DD2EE, 0x4E048354, 0x3903B3C2, 0xA7672661, 0xD06016F7, 0x4969474D, 0x3E6E77DB, 0xAED16A4A, 0xD9D65ADC, 0x40DF0B66, 0x37D83BF0, 0xA9BCAE53, 0xDEBB9EC5, 0x47B2CF7F, 0x30B5FFE9, 0xBDBDF21C, 0xCABAC28A, 0x53B39330, 0x24B4A3A6, 0xBAD03605, 0xCDD70693, 0x54DE5729, 0x23D967BF, 0xB3667A2E, 0xC4614AB8, 0x5D681B02, 0x2A6F2B94, 0xB40BBE37, 0xC30C8EA1, 0x5A05DF1B, 0x2D02EF8D }; unsigned int Crc32(unsigned char * pcBlock, unsigned int len) { unsigned int crc = 0xFFFFFFFF; while (len--) crc = (crc >> 8) ^ Crc32Table[(crc ^ *pcBlock++) & 0xFF]; return crc ^ 0xFFFFFFFF; }
Классификация реализаций алгоритмов CRC
Для точного указания, как именно рассчитывается CRC, чаще всего приходится полностью приводить алгоритм её расчёта.
На самом деле достаточно указать ряд параметров, точно описывающих конкретный частный алгоритм CRC (если это на самом деле CRC).
В модели алгоритма CRC Rocksoft, получившей некоторое хождение, используются следующие параметры:
Name: Это имя, присвоенное данному алгоритму.
Width: Степень алгоритма, выраженная в битах. Она всегда на единицу меньше длины полинома, но равна его степени.
Poly: Собственно полином. Это битовая величина, которая для удобства может быть представлена шестнадцатеричным числом. Старший бит при этом опускается (он всегда 1). Например, если используется полином 10110, то он обозначается числом «06h». Важной особенностью данного параметра является то, что он всегда представляет собой необращенный полином, младшая часть этого параметра во время вычислений всегда является наименее значащими битами делителя.
Init: Этот параметр определяет исходное содержимое регистра на момент запуска вычислений. Данный параметр указывается шестнадцатеричным числом.
RefIn(Revert): Логический параметр. Если он имеет значение False, байты сообщения обрабатываются, начиная с 7 бита, который считается наиболее значащим, а наименее значащим считается бит 0 (сдвиг налево). Если параметр имеет значение True («Истина»), то каждый байт перед обработкой обращается (сдвиг направо).
RefOut: Логический параметр. Если он имеет значение False, то конечное содержимое регистра сразу передается на стадию XorOut, в противном случае, когда параметр имеет значение True, содержимое регистра обращается перед передачей на следующую стадию вычислений. в приведённых алгоритмах, по-видимому, False).
XorOut: W битное значение, обозначаемое шестнадцатеричным числом. Оно комбинируется с конечным содержимым регистра (после стадии RefOut), прежде чем будет получено окончательное значение контрольной суммы.
Check: Это поле, собственно, не является частью определения алгоритма, данное поле служит контрольным значением, которое может быть использовано для слабой проверки правильности реализации алгоритма. Поле содержит контрольную сумму, рассчитанную для ASCII строки «123456789» (шестнадцатеричные значение «313233…»).
После определения всех этих параметров, можно точно описать особенности применённого CRC алгоритма.
Примеры спецификаций некоторых алгоритмов CRC:
Name : CRC 16 Width : 16 Poly : 8005 Init : 0000 RefIn : True RefOut : True XorOut : 0000 Check : BB3D
Name : CRC 16/CITT Width : 16 Poly : 1021 Init : FFFF RefIn : False RefOut : False XorOut : 0000
Name : XMODEM Width : 16 Poly : 8408 Init : 0000 RefIn : True RefOut : True XorOut : 0000
Name : ARC Width : 16 Poly : 8005 Init : 0000 RefIn : True RefOut : True XorOut : 0000
Name : CRC 32 Width : 32 Poly : 04C11DB7 Init : FFFFFFFF RefIn : True RefOut : True XorOut : FFFFFFFF Check : CBF43926
См. также
Ссылки
- Элементарное руководство по CRC алгоритмам обнаружения ошибок
- CRC, и как его восстановить
- Восстановление CRC
- CRC-калькулятор
- Генератор CRC-функций на языках Verilog
- Ross N. Williams/Anarchriz. Всё о CRC32 — Ross N. Williams «Элементарное руководство по CRC алгоритмам обнаружения ошибок»
- Ross N. Williams A PAINLESS GUIDE TO CRC ERROR DETECTION ALGORITHMS (ENG) (Оригинал статьи на английском)
Литература
- Генри С. Уоррен, мл. Глава 5. Подсчет битов // Алгоритмические трюки для программистов = Hacker's Delight. — М.: Вильямс, 2007. — 288 с. — ISBN 0-201-91465-4
Wikimedia Foundation. 2010.