- Код Боуза-Чоудхури-Хоквингема
-
Коды Боуза — Чоудхури — Хоквингхема (БЧХ-коды) — в теории кодирования это широкий класс циклических кодов, применяемых для защиты информации от ошибок (см. Обнаружение и исправление ошибок). Отличается возможностью построения кода с заранее определенными корректирующими свойствами, а именно, минимальным кодовым расстоянием. Коды Рида — Соломона являются частным случаем БЧХ-кодов.
Содержание
Формальное описание
БЧХ-код является циклическим кодом, который можно задать порождающим полиномом. Для его нахождения в случае БЧХ-кода необходимо заранее определить длину кода n (она не может быть произвольной) и требуемое минимальное расстояние
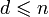 . Найти порождающий полином можно следующим образом.
. Найти порождающий полином можно следующим образом.
Пусть α — примитивный элемент поля GF(qm) (то есть
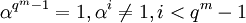 ), пусть β = αs, — элемент поля GF(qm) порядка
), пусть β = αs, — элемент поля GF(qm) порядка 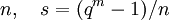 . Тогда нормированный полином g(x) минимальной степени над полем GF(q), корнями которого являются d − 1 подряд идущих степеней
. Тогда нормированный полином g(x) минимальной степени над полем GF(q), корнями которого являются d − 1 подряд идущих степеней 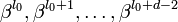 элемента β для некоторого целого l0 (в том числе 0 и 1), является порождающим полиномом БЧХ-кода над полем GF(q) с длиной n и минимальный расстоянием
элемента β для некоторого целого l0 (в том числе 0 и 1), является порождающим полиномом БЧХ-кода над полем GF(q) с длиной n и минимальный расстоянием 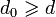 .
.
Число проверочных символов r равно степени g(x), число информационных символов k = n − r, величина d называется конструктивным расстоянием БЧХ-кода. Если n = qm − 1, то код называется примитивным, иначе непримитивным.
Так же, как и для циклического кода, кодовый полином c(x) может быть получен из информационного полинома m(x), степени не больше k − 1, путем перемножения m(x) и g(x):
c(x) = m(x)g(x).
Построение
Для нахождения порождающего полинома необходимо выполнить несколько этапов:
- выбрать q, то есть поле GF(q), над которым будет построен код;
- выбрать длину n кода из условия n = (qm − 1) / s, где m,s — целые положительные числа;
- задать величину d конструктивного расстояния;
1) построить циклотомические классы элемента β = αs поля GF(qm) над полем GF(q), где α — примитивный элемент GF(qm);
2) поскольку каждому такому циклотомическому классу соответвует неприводимый полином над GF(q), корнями которого являются элементы этого и только этого класса, со степенью равной количеству элементов в классе, то выбрать
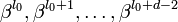 таким образом, чтобы суммарная длина циклотомических классов была минимальна
таким образом, чтобы суммарная длина циклотомических классов была минимальна3) вычислить порождающий полином
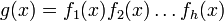 , где fi(x) — полином, соответсвующий i-ому циклотомическому классу
, где fi(x) — полином, соответсвующий i-ому циклотомическому классуПримеры кодов
Примитивный 2-ичный (15,7,5) код
Пусть q = 2, требуемая длина кода n = 24 − 1 = 15 и минимальное расстояние
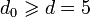 . Возьмем α — примитивный элемент поля GF(16), и α,α2,α3,α4 — четыре подряд идущих степеней элемента α. Они принадлежат двум циклотомическим классам над полем GF(2), которым соответсвуют неприводимые полиномы f1(x) = x4 + x + 1 и f2(x) = x4 + x3 + x2 + x + 1. Тогда полином
. Возьмем α — примитивный элемент поля GF(16), и α,α2,α3,α4 — четыре подряд идущих степеней элемента α. Они принадлежат двум циклотомическим классам над полем GF(2), которым соответсвуют неприводимые полиномы f1(x) = x4 + x + 1 и f2(x) = x4 + x3 + x2 + x + 1. Тогда полиномg(x) = f1(x)f2(x) = x8 + x7 + x6 + x4 + 1 имеет в качестве корней элементы α,α2,α3,α4 и является порождающим полиномом БЧХ-кода с параметрами (15,7,5).
16-ричный (15,11,5) код (код Рида — Соломона)
Пусть n = q − 1 = 15 и α — примитивный элемент GF(16). Тогда
g(x) = (x − α)(x − α2)(x − α3)(x − α4) = x4 + α13x3 + α6x2 + α3x + α10
.
Каждому элементу поля GF(16) можно сопоставить 4 битам, поэтому одно кодовое слово эквивалентно 60=15*4 битам, таким образом набору из 44 бит ставится в соответствие набор из 60 бит. Можно сказать, что такой код работает с полубайтами информации.
Кодирование
Для кодирования кодами БЧХ применяются те же методы, что и для кодирования циклическими кодами.
Методы декодирования
Коды БЧХ являются циклическими кодами, поэтому к ним применимы все методы, используемые для декодирования циклических кодов. Однако существуют гораздо лучшие алгоритмы, разработанные именно для БЧХ-кодов.
Исторически первым методом декодирования был найден Питерсоном для двоичного случая (q = 2), затем Горенстейном и Цирлером для общего случая. Упрощение алгоритма было найдено Берлекэмпом, а затем усовершенствовано Месси (алгоритм Берлекэмпа — Месси). Существует отличный от этих методов декдирования — метод основанный на алгоритме Евклида.
Алгоритм Питерсона — Горенстейна — Цирлера (ПГЦ)
Пусть БЧХ код над полем GF(q) длины n и с конструктивным расстоянием d задается порождающим полиномом g(x), который имеет среди своих корней элементы
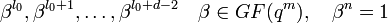 ,
, 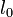 — целое число (например 0 или 1). Тогда каждое кодовое слово обладает тем свойством, что
— целое число (например 0 или 1). Тогда каждое кодовое слово обладает тем свойством, что 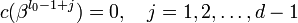 . Принятое слово r(x) можно записать как r(x) = c(x) + e(x), где e(x) — полином ошибок. Пусть произошло
. Принятое слово r(x) можно записать как r(x) = c(x) + e(x), где e(x) — полином ошибок. Пусть произошло 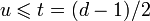 ошибок на позициях
ошибок на позициях 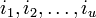 (t максимальное число исправляемых ошибок), значит
(t максимальное число исправляемых ошибок), значит 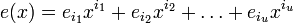 , а
, а 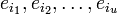 — величины ошибок.
— величины ошибок.Можно составить j-ый синдром Sj принятого слова r(x):
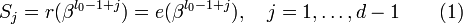 .
.Задача состоит в нахождений числа ошибок u, их позиций
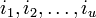 и их значений
и их значений 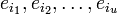 при известных синдромах Sj.
при известных синдромах Sj.Предположим, для начала, что u в точности равно t. Запишем (1) в виде системы нелинейных(!) уравнений в явном виде:
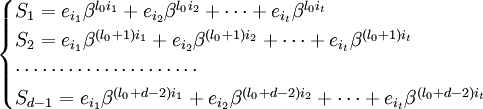
Обозначим через
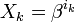 локатор k-ой ошибки, а через
локатор k-ой ошибки, а через 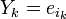 величину ошибки,
величину ошибки, 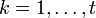 . При этом все Xk различны, так как порядок элемента β равен n, и поэтому при известном Xk можно определить ik как ik = logβXk.
. При этом все Xk различны, так как порядок элемента β равен n, и поэтому при известном Xk можно определить ik как ik = logβXk.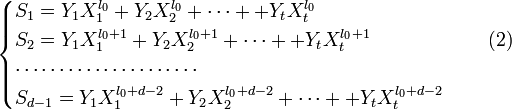
Составим полином локаторов ошибок:
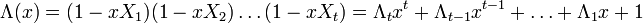
Корнями этого полинома являются элементы, обратные локаторам ошибок. Помножим обе части этого полинома на
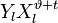 . Полученное равенство будет справедливо для
. Полученное равенство будет справедливо для 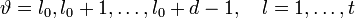 :
: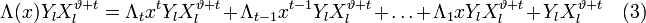
Положим
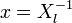 и подставим в (3). Получится равенство, справедливое для каждого
и подставим в (3). Получится равенство, справедливое для каждого 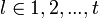 и при всех
и при всех 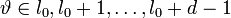 :
: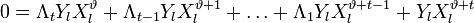
Таким образом для каждого l можно записать свое равенство. Если их просуммировать по l, то получиться равенство, справедливое для каждого
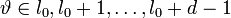 :
: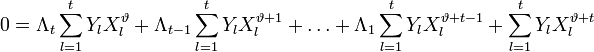 .
..
Учитывая (2) и то, что
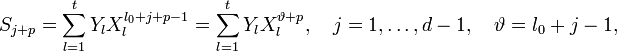 (то есть
(то есть 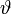 меняется в тех же пределах, что и ранее) получаем систему линейных уравнений:
меняется в тех же пределах, что и ранее) получаем систему линейных уравнений: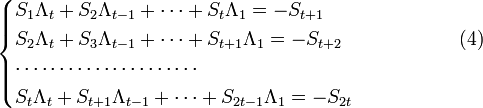
.
Или в матричной форме
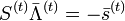
,
где
![S^{(t)}={ \left[ \begin{matrix}
S_1 & S_2 & \dots & S_t \\
S_2 & S_3 & \dots & S_{t+1} \\
\cdots & \cdots & \cdots & \\
S_t & S_{t+1} & \dots & S_{2t-1}
\end{matrix} \right] }, \quad \quad \quad \quad \quad\quad(5)](/pictures/wiki/files/99/cb1fb0775da4988ff94bb8f82afbb614.png)
![\bar\Lambda^{(t)} =
{ \left[ \begin{matrix}
\Lambda_t \\
\Lambda_{t-1} \\
\cdots \\
\Lambda_1
\end{matrix} \right] },
\quad \quad
\bar s^{(t)}
{ \left[ \begin{matrix}
S_{t+1} \\
S_{t+2} \\
\cdots \\
S_{2t}
\end{matrix} \right] }](/pictures/wiki/files/102/fb3abb36e14beb74ecaab8e8af0df01e.png)
Если число ошибок и в самом деле равно t, то система (4) разрешима, и можно найти значения коэффициентов
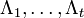 . Если же число u < t, то определитель матрицы S(t) системы (4) будет равен 0. Это есть признак того, что количество ошибок меньше t. Поэтому необходимо составить систему (4), предполагая число ошибок равным t − 1. Высчитать определитель новой матрицы S(t − 1) и т. д., до тех пор, пока не установим истинное число ошибок.
. Если же число u < t, то определитель матрицы S(t) системы (4) будет равен 0. Это есть признак того, что количество ошибок меньше t. Поэтому необходимо составить систему (4), предполагая число ошибок равным t − 1. Высчитать определитель новой матрицы S(t − 1) и т. д., до тех пор, пока не установим истинное число ошибок.После этого можно решить систему (4) и получить коэффициенты полинома локаторов ошибок. Его корни (элементы, обратные локаторам ошибок) можно найти простым перебором по всем элементам поля GF(qm). К ним найти элементы, обратные по умножению, — это локаторы ошибок
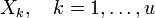 . По локаторам можно найти позиции ошибок (ik = logβXk), а значения Yk ошибок из системы (2), приняв t = u. Декодирование завершено.
. По локаторам можно найти позиции ошибок (ik = logβXk), а значения Yk ошибок из системы (2), приняв t = u. Декодирование завершено.См. также
- Обнаружение и исправление ошибок
- Конечное поле
- Многочлен над конечным полем
- Матрица Вандермонда
- Линейный код
- Циклический код
- Код Рида — Соломона
Литература
- Блейхут Р. Теория и практика кодов, контролирующих ошибки = Theory and practice of error control codes. — М.: Мир, 1986. — С. 576.
- Питерсон У., Уэлдон Э. Коды, исправляющие ошибки. — М.: Мир, 1976. — С. 596.
Wikimedia Foundation. 2010.
