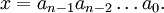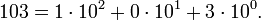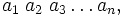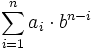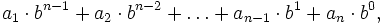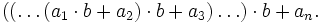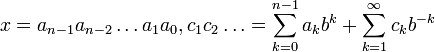Позиционные системы счисления

Позиционная систе́ма счисле́ния — система счисления, в которой один и тот же числовой знак (цифра) в записи числа имеет различные значения в зависимости от того места (разряда), где он расположен. Изобретение позиционной нумерации, основанной на поместном значении цифр, приписывается шумерам и вавилонянам; развита была такая нумерация индусами и имела неоценимые последствия в истории человеческой цивилизации. К числу таких систем относится современная десятичная система счисления, возникновение которой связано со счётом на пальцах. В средневековой Европе она появилась через итальянских купцов, в свою очередь заимствовавших её у мусульман.

Определение

Каждая позиционная система счисления определяется некоторым числом b (т. н. основание системы счисления) с | b | > 1. Система счисления с основанием b также называется b-ричной (в частности, двоичной, троичной, десятичной и т. п.).

Целое число x в b-ричной системе счисления представляется в виде конечной линейной комбинации степеней числа b:

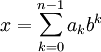$x = \sum_{k=0}^{n-1} a_k b^k$, где a_k — это целые числа, называемые цифрами, удовлетворяющие неравенству $0 \leq a_k < |b|$.

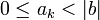Каждая степень b^k в такой записи называется разрядом (позицией), старшинство разрядов и соответствующих им цифр определяется значением показателя степени k. Обычно для ненулевого числа x требуют, чтобы старшая цифра a_{n − 1} в b-ричном представлении x была также ненулевой.

Если не возникает разночтений (например, когда все цифры представляются в виде уникальных письменных знаков), число x записывают в виде последовательности его b-ричных цифр, перечисляемых по убыванию старшинства разрядов слева направо:

$x = a_{n-1} a_{n-2}\dots a_0.$

Например, число сто три представляется в десятичной системе счисления в виде:

$103 = 1 \cdot 10^{2} + 0 \cdot 10^{1} + 3 \cdot 10^{0}.$

Примеры позиционных систем счисления

• 1 — единичная (унарная) система счисления, может рассматриваться как вырожденный случай позиционной системы счисления.
• 2 — двоичная (в дискретной математике, информатике, программировании)
• 3 — троичная система счисления
• 8 — восьмеричная (в программировании)
• 10 — десятичная система счисления
• 12 — двенадцатеричная (широко использовалась в древности, в некоторых частных областях используется и сейчас)
• 16 — шестнадцатеричная (наиболее распространена в программировании, а также в шрифтах)
• 40 — сорокаичная система счисления (применялась в древности («сорок сороков = 1600»))
• 60 — шестидесятеричная (измерение углов и, в частности, долготы и широты)

Запись чисел

Для записи чисел системы счисления с основанием до 36 включительно в качестве цифр (знаков) используются арабские цифры (0, 1, 2, 3, 4, 5, 6, 7, 8, 9) и затем буквы латинского алфавита (a, b, c, d, e, f, g, h, i, j, k, l, m, n, o, p, q, r, s, t, u, v, w, x, y, z). При этом, a = 10, b = 11 и т. д., иногда x = 10.

При одновременной работе с несколькими системами счисления для их различения основание системы обычно указывается в виде нижнего индекса, который записывается в десятичной системе:

123₁₀ — это число 123 в десятичной системе счисления;

1111011₂ — то же число, но в двоичной системе.

В некоторых специальных областях применяются особые правила указания основания. Например, в программировании шестнадцатеричная система обозначается:

• в ассемблере и записях общего рода, не привязанных к конкретному языку, буквой h (от hexadecimal) в конце числа (синтаксис Intel);
• в Паскале знаком «$» в начале числа;
• в C и многих других языках комбинацией 0x или 0X (от hexadecimal) в начале.

В некоторых диалектах языка Си по аналогии с «0x» используется префикс «0b» для обозначения двоичных чисел. (Обозначение «0b» не входит в стандарт ANSI C.)

Плотность записи чисел

1. Описание по С.В.Фомину (подобное же описание приводится в работе А.Кушнерова ^[1] со ссылкой на малоизвестную теорему Джона фон Неймана 1946 г. "о компактности систем счисления", но в этой работе на рис.1 приводится график для фиксированного числа знаков $n=8\,$.)

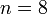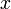$x\,$ - основание системы счисления (число знаков (цифр) в одном разряде, число устойчивых состояний триггера) ($b\,$)

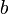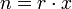$n=r \cdot x\,$ - число знаков (число элементов, число инверторов в одном триггере) (в трёхразрядном (трёхпозиционном) десятичном числе 30 знаков) (экономичность системы)

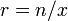$r=n/x\,$ - число разрядов (число позиций, длина разрядной сетки, число разрядов регистра, число триггеров в регистре)

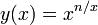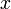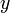Число записываемых (представимых, представляемых) чисел $y(x)=x^{n/x}\,$, график функции с различными масштабами по осям $x\,$ и $y\,$ изображён на рис.4. (Функция не обобщена и зависит от числа знаков - 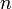$n\,$, поэтому приводится график для одного, фиксированного числа знаков - 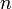$n\,$, значение которого не приводится).

Необходимое условие того, что в данной точке 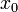$x_0\,$ функция 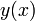$y(x)\,$ достигает максимума, состоит в обращении в нуль её производной в этой точке. В данном случае производная этой функции равна $dy/dx=-n \cdot x^{n/x} \cdot ln(x)/x^2+(n/x) \cdot x^{n/x-1}=n \cdot x^{n/x-2} \cdot (1-ln(x))\,$.

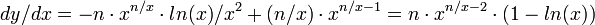Приравняв её нулю, получим, что 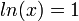$ln(x)=1\,$, т.е. $x=e\,$.

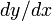Так как слева от точки $x=e\,$ производная $dy/dx\,$ положительна, а справа отрицательна, то, в силу известных теорем дифференциального исчисления, в этой точке наша функция действительно имеет максимум.

Экономичность системы счисления - немаловажное обстоятельство с точки зрения её использования в вычислительной машине. Поэтому, хотя применение в вычислительной машине троичной системы вместо двоичной влечёт некоторые конструктивные трудности (при этом нужно пользоваться элементами, каждый из которых может находиться не в двух, а в трёх устойчивых состояниях), эта система уже была использована в некоторых реально существующих вычислительных устройствах.^[2]

2. Описание через информационную энтропию

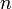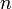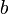При условии равновероятности появления каждой из цифр в записи числа информационная энтропия записи $n\,$-значного (в данном случае автор употребил слово $n\,$-значного в смысле $r\,$-разрядного, $r\,$-позиционного) числа в системе счисления с основанием $b\,$ принимает значение 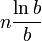$n\frac{\ln b}{b}$ (с точностью до постоянного коэффициента). Поэтому плотность записи (то есть количество информации на одну позицию) чисел в системе счисления с основанием 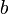$b\,$ равна $\frac{\ln(b)}{b}$.

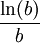Плотность записи, как функция от 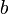$b\,$, принимает максимальное значение в точке при $b=e=2,718281828\ldots$.

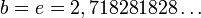Таким образом, наибольшей плотностью записи чисел (информации) обладает система счисления с нецелочисленным основанием $e\,$. Из систем счисления с целочисленными основаниями наибольшей плотностью записи чисел (информации) обладает троичная система счисления. Двоичная и четверичная системы счисления делят второе место. Остальные целочисленные системы счисления имеют меньшую плотность записи чисел (информации).

3. Более простое описание независимое от числа знаков (элементов) - $n\,$

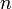
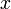$x\,$ - основание системы счисления (число знаков (цифр) в одном разряде, число устойчивых состояний триггера) ($b\,$)

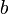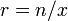$r=n/x\,$ - число разрядов (число позиций, длина разрядной сетки, число разрядов регистра, число триггеров в регистре)

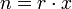$n=r \cdot x\,$ - число знаков (число элементов, число инверторов в одном триггере) (в трёхразрядном (трёхпозиционном) десятичном числе 30 знаков) (экономичность системы)

Число записывыемых (представимых, представляемых) чисел (кодов) $y(x)=x^{r}\,$

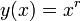
Натуральный логарифм числа представимых чисел (кодов) $ln(y(x))=r \cdot ln(x)\,$

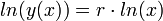
Удельная натуральнологарифмическая плотность записи чисел 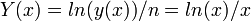$Y(x)=ln(y(x))/n=ln(x)/x\,$[натуральный логарифм числа представимых чисел/число знаков (элементов)] наибольшая в точке экстремума, в которой первая производная равна нулю.

Первая производная от натуральнологарифмической плотности записи чисел 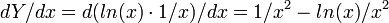$dY/dx=d(ln(x) \cdot 1/x)/dx=1/x^2-ln(x)/x^2$ равна нулю в точке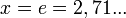 $x=e=2,71...\,$

Таким образом, наибольшей логарифмической плотностью записи чисел (кодов, информации) обладает система счисления с нецелочисленным основанием равным числу Эйлера - 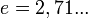$e=2,71...\,$ . Из систем счисления с целочисленными основаниями наибольшей плотностью записи чисел (кодов, информации) обладает троичная система счисления. Двоичная и четверичная системы счисления делят второе место. Остальные целочисленные системы счисления имеют меньшую плотность записи чисел (кодов, информации).

Число знаков на запись чисел (аппаратные затраты)

1. По О.А.Акулову и Н.В.Медведеву (приведены обозначения по первоисточнику и общие обозначения):

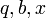$q, b, x\,$ - основание системы счисления (число знаков (цифр) в одном разряде, число устойчивых состояний триггера)

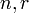$n, r\,$ - число разрядов (число позиций, длина разрядной сетки, число разрядов регистра, число триггеров в регистре)

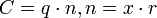$C=q \cdot n, n=x \cdot r$ - число элементов (экономичность системы) (число знаков, число инверторов в одном триггере)

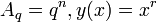$A_q=q^n, y(x)=x^r\,$ - число представляемых (записываемых, представимых) чисел

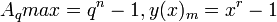$A_qmax=q^n-1, y(x)_m=x^r-1\,$ - наибольшее представляемое (записываемое, представимое) число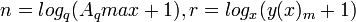

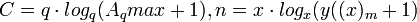
$n=log_q(A_qmax+1), r=log_x(y(x)_m+1)\,$

$C=q \cdot log_q(A_qmax+1), n=x \cdot log_x(y((x)_m+1)\,$

$F=q \cdot log_q(A_qmax+1)/[2 \cdot log_2(A_2max+1)], F=x \cdot log_x(y(x)_m+1)/[2 \cdot log_2(y(2)_m+1)]$ - относительные аппаратные затраты (экономичность системы счисления) по Акулову и Медведеву

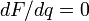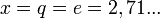Минимальные относительные аппаратные затраты будут при $dF/dq=0\,$ при $x=q=e=2,71...\,$.^[3]

2. Более простое описание:

Аппаратные затраты являются функцией обратной функции натуральнологарифмической плотности записи чисел, поэтому, поделив 1 на функцию натуральнологарифмической плотности записи чисел получим более простое выражение функции натуральнологарифмических аппаратных затрат:

$Z=1/(ln(x)/x)=x/ln(x)\,$

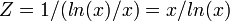
Свойства

Позиционная система счисления обладает рядом свойств:

1. Основание системы счисления в ней самой всегда записывается как 10; например, в двоичной системе счисления 10 означает число 2.
2. Для записи числа x в b-ричной системе счисления требуется 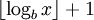$\lfloor\log_b x\rfloor + 1$ цифр, где $\lfloor\cdot\rfloor$ означает взятие целой части числа.
3. Сравнение чисел. Сравним числа 321 и 312. Для этого слева направо сравниваем цифры, стоящие в одинаковых разрядах: 3 = 3 — результат сравнения чисел не определён; 2 > 1 — первое число больше независимо от оставшихся цифр.
4. Сложение чисел. Сложим 321 и 312. Для этого справа налево складываем отдельные цифры:

1 + 2 = 3

2 + 1 = 3

3 + 3 = 6, итого 633.

Таким же образом можно сложить числа произвольной длины.

Переход к другому основанию

Перевод произвольной позиционной системы счисления в десятичную

Если число в b-ричной системе счисления равно

$a_1\;a_2\;a_3 \ldots a_n,$

то для перевода в десятичную систему вычисляем такую сумму:

$\sum_{i=1}^n a_i\cdot b^{n-i}$

или, в более наглядном виде:

$a_1\cdot b^{n-1} + a_2 \cdot b^{n-2} + \ldots + a_{n-1} \cdot b^1 + a_n \cdot b^0,$

либо, наконец, в виде схемы Горнера:

$((\ldots(a_1 \cdot b + a_2) \cdot b + a_3) \ldots ) \cdot b + a_n.$

Например:

101100₂ =

= 1 · 2⁵ + 0 · 2⁴ + 1 · 2³ + 1 · 2² + 0 · 2¹ + 0 · 1 =

= 1 · 32 + 0 · 16 + 1 · 8 + 1 · 4 + 0 · 2 + 0 · 1 =

= 32 + 8 + 4 + 0 = 44₁₀

Пример на C для перевода 18 в 7-ричную систему выглядит так (корректно работает до основания 10, дальше появятся «цифры» :;<=>?@012 и т. д.):

void perevod( unsigned int num, unsigned int base )
{
  #define LENGTH ( 8 * sizeof( unsigned int ) ) /* размер с запасом */
 
  char str[ LENGTH + 1]; /* +1 для символа [[EOS]] */
  char *pstr = str + LENGTH - 1; /* начинаем заполнять цифрами с конца */
 
  str[ LENGTH ] = '\0'; /* добавляем EOS */
 
  if( num == 0 ) *pstr = '0'; /* если цикл не будет крутиться */
  else
    do
    {
      *pstr-- = '0' + num % base; /* заполняем цифрами, сдвигаясь влево */
      num /= base;
    }
    while( num > 0 );
 
  printf( "%s\n", pstr + 1 ); /* печатаем, начиная с 1го ненулевого символа */
 
  #undef LENGTH /* уже не нужно */
}
 
void main()
{
  perevod( 18, 7 );
}

Перевод из десятичной в произвольную позиционную систему счисления

Для перевода необходимо делить число с остатком на основание счисления до тех пор, пока частное больше основания счисления.

Пример:

4410 переведём в двоичную систему
44 делим на 2. частное 22, остаток 0
22 делим на 2. частное 11, остаток 0
11 делим на 2. частное  5, остаток 1
 5 делим на 2. частное  2, остаток 1
 2 делим на 2. частное  1, остаток 0
 1 делим на 2. частное  0, остаток 1
Частное равно нулю, деление закончено. Теперь записав все остатки справа налево получим число 1011002

Перевод из двоичной в восьмеричную и шестнадцатеричную системы

Для этого типа операций существует упрощенный алгоритм.

Для восьмеричной — разбиваем число на триплеты, преобразуем триплеты по таблице

000 0 100 4
001 1 101 5
010 2 110 6
011 3 111 7

Для шестнадцатеричной — разбиваем на квартеты, преобразуем по таблице

0000 0 0100 4 1000 8 1100 C 
0001 1 0101 5 1001 9 1101 D
0010 2 0110 6 1010 A 1110 E
0011 3 0111 7 1011 B 1111 F

Пример:

преобразуем 1011002
восьмеричная — 101 100 → 548
шестнадцатеричная — 0010 1100 → 2C16

Перевод из восьмеричной и шестнадцатеричной систем в двоичную

Для этого типа операций существует упрощенный алгоритм-перевёртыш.

Для восьмеричной — преобразуем по таблице в триплеты

0 000 4 100
1 001 5 101
2 010 6 110
3 011 7 111

Для шестнадцатеричной — преобразуем по таблице в квартеты

0 0000 4 0100 8 1000 C 1100 
1 0001 5 0101 9 1001 D 1101
2 0010 6 0110 A 1010 E 1110
3 0011 7 0111 B 1011 F 1111

Пример:

преобразуем
548 → 101 100
2C16 → 0010 1100

См. также: Таблица порядков двоичных, шестнадцатеричных и десятичных чисел

Перевод из произвольной системы счисления в десятичную

Рассмотрим пример перевода двоичного числа 1100,011₂ в десятичное. Целая часть этого числа равна 12 (см. выше), а вот перевод дробной части рассмотрим подробнее:

$0,011 = 0 \cdot 2^{-1} + 1 \cdot 2^{-2} + 1 \cdot 2^{-3} = 0 + 0,25 + 0,125 = 0,375.$

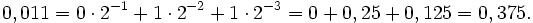
Итак, число 1100,011₂ = 12,375₁₀.

Точно также осуществляется перевод из любой системы счисления, только вместо «2» ставится основание системы.

Для удобства перевода, целую и дробную части числа переводят отдельно, а результат потом суммируют.

Перевод из двоичной системы в 8- и 16-ричную

Перевод дробной части из двоичной системы счисления в системы счисления с основаниями 8 и 16 осуществляется точно также, как и для целых частей числа, за тем лишь исключением, что разбивка на октавы и тетрады идёт вправо от десятичной запятой, недостающие разряды дополняются нулями справа. Например, рассмотренное выше число 1100,011₂ будет выглядеть как 14,3₈ или C,6₁₆.

Перевод из десятичной системы в произвольную

Для перевода дробной части числа в другие системы счисления нужно обратить целую часть в нуль и начать умножение получившегося числа на основание той системы, в которую нужно перевести. Если в результате умножения будут снова появляться целые части, их нужно повторно обращать в нуль, предварительно запомнив (записав) значение получившейся целой части. Операция заканчивается, когда дробная часть полностью обратится в нуль. Ниже приводится пример перевода числа 103,625₁₀ в двоичную систему счисления.

Переводим целую часть по правилам, описанным выше, получаем 10310 = 11001112.
0,625 умножаем на 2. Дробная часть 0,250. Целая часть 1.
0,250 умножаем на 2. Дробная часть 0,500. Целая часть 0.
0,500 умножаем на 2. Дробная часть 0,000. Целая часть 1.
Итак, сверху вниз получаем число 1012
103,62510 = 1100111,1012

Точно также осуществляется перевод в системы счисления с любым основанием.

Сразу нужно отметить, что этот пример специально подобран, в общем случае очень редко удаётся завершить перевод дробной части числа из десятичной системы в другие системы счисления, а потому, в подавляющем большинстве случаев, перевод можно осуществить с какой либо долей погрешности. Чем больше знаков после запятой — тем точнее приближение результата перевода к истине. В этих словах легко убедиться, если попытаться, например, перевести в двоичный код число 0,626.

Вариации и обобщения

Запись рациональных чисел

Рациональное число x в b-ричной системе счисления представляется в виде линейной комбинации (вообще говоря, бесконечной) степеней числа b:

$x = a_{n-1} a_{n-2} \ldots a_1 a_0 , c_1 c_2 \ldots = \sum_{k=0}^{n-1} a_k b^k + \sum_{k=1}^{\infty} c_k b^{-k}$

где a_k — цифры целой части (до запятой), c_k — цифры дробной части (после запятой), n — число разрядов целой части.

Конечной записью в b-ричной системе счисления обладают только рациональные числа, представимые в виде 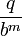$\frac{q}{b^m}$, где m и q — целые числа; рациональные числа, не представимые в таком виде, записываются в виде периодических дробей.

Симметричные позиционные системы счисления

Такие системы счисления отличаются от обычных тем, что используют цифры не из множества 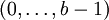$(0, \ldots, b-1)$, а из множества 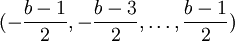$(-\frac{b-1}{2}, -\frac{b-3}{2}, \ldots, \frac{b-1}{2})$. Чтобы цифры были целыми, нужно, чтобы b было нечётным. В симметричных системах счисления не требуется дополнительных обозначений для знака числа. Кроме того, вычисления в симметричных системах удобны тем, что не требуется особых правил округления — оно сводится к простому отбрасыванию лишних разрядов, что резко уменьшает систематические ошибки вычислений.

Чаще всего используется симметричная троичная система счисления с цифрами (-1,0,1). Она применяется в троичной логике и была технически реализована в вычислительной машине «Сетунь».

Отрицательные основания

Основная статья: Нега-позиционная система счисления

Существуют позиционные системы с отрицательными основаниями, называемые нега-позиционными:

• -2 — нега-двоичная система счисления
• -10 — нега-десятичная система счисления

Нецелочисленные основания

Иногда также рассматривают позиционные системы с нецелочисленными основаниями:

• 1,61… =Ф — система счисления Бергмана с иррациональным основанием равным числу Фидия, или «золотое сечение».^[4]
• 2,71… = е — е-ричная система счисления с основанием, равным числу Эйлера. Такая система счисления называется натуральной, а её разряд называется нат.

Примечания

1. ↑ http://314159.ru/kushnerov/kushnerov1.pdf Троичная цифровая техника. Ретроспектива и современность
2. ↑ http://www.math.ru/lib/files/plm/v40.djvu Популярные лекции по математике. С.В.Фомин. Системы счисления. § 14. Об одном замечательном свойстве троичной системы, стр.39-40.
3. ↑ О. А. Акулов, Н. В. Медведев. Информатика и вычислительная техника. 4-е изд. — М.: Омега-Л, 2007. (Раздел I, Гл.3.3)
4. ↑ А. В. Никитин Система Бергмана.

Ссылки

• Л. Н. Беляева. Системы счисления и признаки делимости
• С. Б. Гашков. Системы счисления и их применение Библиотека «Математическое просвещение», выпуск 29, 2004.
• Яглом И. Системы счисления Квант № 6, 1970.
• Что такое система счисления?
• http://ito.edu.ru/2004/Moscow/I/1/I-1-3731.html О преподавании темы "Новые системы счисления". Федотов Валерий Павлович. Северо-Западный институт печати, г. Санкт-Петербург
• Online Кодировщик чисел в разные позиционые системы счисления