- Подполе
-
По́лем называется множество F с двумя бинарными операциями + (аддитивная операция или сложение) и
 (мультипликативная операция или умножение), если оно (вместе с этими операциями) образует коммутативное ассоциативное кольцо c единицей
(мультипликативная операция или умножение), если оно (вместе с этими операциями) образует коммутативное ассоциативное кольцо c единицей 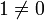 , все ненулевые элементы которого обратимы.
, все ненулевые элементы которого обратимы.Иными словами, множество F с двумя бинарными операциями + (сложение) и
 (умножение) называется полем, если оно образует коммутативную группу по сложению, все его ненулевые элементы образуют коммутативную группу по умножению, и выполняется свойство дистрибутивности.
(умножение) называется полем, если оно образует коммутативную группу по сложению, все его ненулевые элементы образуют коммутативную группу по умножению, и выполняется свойство дистрибутивности.Содержание
Связанные определения
- Характеристика поля — наименьшее положительное целое n число такое, что сумма n копий единицы равна нулю:
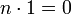
Если такого числа не существует то характеристика равна 0 по определению. - Подполем поля k называется подмножество, которое само является полем относительно операций сложения и умножения, заданных в k.
- Расширение поля — поле, содержащее данное поле в качестве подполя.
Свойства
- Характеристика поля всегда 0 или простое число.
- Поле характеристики 0 содержит подполе изоморфное полю рациональных чисел
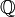 .
. - Поле простой характеристики p содержит подполе изоморфное полю вычетов
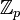 .
.
- Поле характеристики 0 содержит подполе изоморфное полю рациональных чисел
- Количество элементов в конечном поле всегда равно pn, степени простого числа.
- При этом для любого числа вида pn существует единственное (с точностью до изоморфизма) поле из pn элементов, обычно обозначаемое
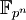 .
.
- При этом для любого числа вида pn существует единственное (с точностью до изоморфизма) поле из pn элементов, обычно обозначаемое
- Любой ненулевой гомоморфизм полей является вложением.
- В поле нет делителей нуля.
Примеры
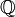 — рациональные числа,
— рациональные числа, — вещественные числа,
— вещественные числа,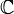 — комплексные числа,
— комплексные числа,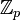 — поле вычетов по модулю p, где p — простое число.
— поле вычетов по модулю p, где p — простое число.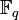 — конечное поле из q = pk элементов, где p — простое число, k — натуральное.
— конечное поле из q = pk элементов, где p — простое число, k — натуральное.
См.также
Ссылки
- Характеристика поля — наименьшее положительное целое n число такое, что сумма n копий единицы равна нулю:
Wikimedia Foundation. 2010.
