- МЕРОМОРФНАЯ ФУНКЦИЯ
- МЕРОМОРФНАЯ ФУНКЦИЯ
-
- аналитическая функция, не имеющая в комплексной плоскости особенностей кроме полюсов. В частности, любая целая функция или рациональная ф-ция является M. ф. Кол-во полюсов у M. ф. не более чем счётно. Если M. f. f(z) имеет конечное число полюсов и выполнена оценка
при нек-рых R> 0, С> 0 и 
- рациональная ф-ция. Если M. ф. имеет бесконечное число полюсов, расположенных в точках 
то обязательнопри 
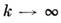Для того чтобы f(z) была M. ф., необходимо и достаточно, чтобы она представлялась в виде отношения двух целых ф-ций.Справедлива теорема Миттаг-Леффле-р а. Пусть задана нек-рая конечная или бесконечная последовательность точек
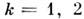... и последовательность комплексных чисел 
..., mk. Тогда существует M. ф. h(z), к-рая имеет полюсы только в точках
..., причём гл. часть Лорана ряда f(z) в точке
совпадает с ф-цией 
Ф-цию h(z )можно представить в виде суммы ряда
где
... - нек-рые полиномы. Обратно, всякая M. f. f(z), имеющая полюсы в точках 
k =1, 2 ... с гл. частями ряда Лорана hk (z), отличается от ф-ции h(z )на целую ф-цию.Напр., ф-ция
является M. ф. и имеет простые полюсы в точках 
, 
, ... с гл. частями 
Для неё имеет место представление 
M. ф.
имеет полюсы второго порядка в тех же точках 
с гл. частями ряда Лорана 
. Соответственно разложение для неё имеет вид 
Лит. см. при ст. Аналитическая функция. Б. И. Завьялов.
Физическая энциклопедия. В 5-ти томах. — М.: Советская энциклопедия. Главный редактор А. М. Прохоров. 1988.
.
