- ГРИНА - КУБО ФОРМУЛЫ
- ГРИНА - КУБО ФОРМУЛЫ
-
- выражают кинетические коэффициенты линейных диссипативных процессов (диффузии, вязкости, теплопроводности) через временные корреляционные функции потоков (вещества, импульса, тепла). Установлены в 1952-54 M. Грином (M. Green) с помощью теории марковских процессов и в 1957 P. Кубо (R. Kubo) с помощью теории реакции статистич. системы на внеш. возмущения. Г.- К. ф. применимы к газам, жидкостям и твёрдым телам как для классич., так и для квантовых систем и являются одним из наиб. важных результатов статистич. теории необратимых процессов.
Коэф. самодиффузии D, теплопроводности
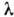, сдвиговой вязкости 
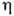, объёмной вязкости 
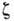равны
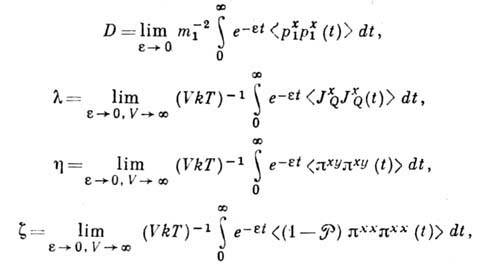
где T - абс. темп-pa, t - время, V - объём,
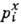-x -комонента импульса i -й частицы, 
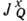-компонента потока тепла, 
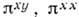-компоненты тензора потока полного импульса,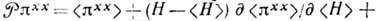
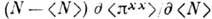, H - гамильтониан системы, N - полное число частиц. Предельный переход 
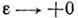совершается после вычисления предела 
Потоки тепла и импульса являются динамич. переменными, зависящими от координат и импульсов всех частиц системы, изменяющихся согласно ур-ниям движения,
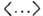означает усреднение по равновесному распределению Гиббса. В квантовом случае в Г.- К. ф. надо заменить t на t - i
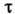и выполнить интегрирование по параметру 
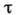в пределах от 0 до 
.
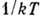Общий характер Г.- К. ф. связан с тем, что для всех макроскопич. систем при малых отклонениях от статистич. равновесия устанавливается квазиравновесная ф-ция распределения, подобная ф-ции распределения Гиббса, параметры к-рой (темп-pa, хим. потенциал и др.) зависят от координат и времени. Решение ур-ния Лиувилля даёт в первом приближении поправку к квазиравновесной ф-ции распределения, пропорциональную градиентам темп-ры и хим. потенциала с коэф., к-рые можно записать в виде Г.- К. ф. T. о., Г.- К. ф. дают микроскопич. выражения для кинетич. коэф. Частным случаем Г.- К. ф. являются Кубо формулы, к-рые выражают реакцию неравновесных ср. физ, величин через запаздывающие Грина функции, связывающие изменения наблюдаемых величин с вызывающим их внеш. возмущением. Иногда Г.- К. ф. наз. ф-лами Кубо.
Лит.: Вопросы квантовой теории необратимых процессов, пер. с англ., M., 1961; Термодинамика необратимых процессов, пер. с англ., M., 1962; Зубарев Д. H., Неравновесная статистическая термодинамика, M., 1971; Форстер Д., Гидродинамические флуктуации, нарушенная симметрия и корреляционные функции, пер. с англ., M., 1980. Д. H. Зубарев.
Физическая энциклопедия. В 5-ти томах. — М.: Советская энциклопедия. Главный редактор А. М. Прохоров. 1988.
.
