КУБО ФОРМУЛЫ

КУБО ФОРМУЛЫ

- выражает линейную реакцию статистической системы на переменное внешнее возмущение. К. ф. позволяют выразить кинетические коэффициенты через равновесные временные корреляционные функции потоков. Установлены Р. Кубо (R. Kubo) в 1957.

При выводе К. ф. предполагается, что система описывается статистич. оператором ( матрицей плотности) 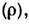удовлетворяющим квантовому Лиувилля уравнению, 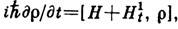и при 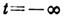находится в состоянии статистич. равновесия, к-рому соответствует равновесный статистич. оператор 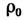канонич. или большого канонич. ансамбля Гиббса. под влиянием адиабатич. включения внеш. поля (механич. возмущения), к-рому соответствует возмущение 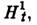ср. значение динамич. переменной А к моменту времени t в линейном по H¹_t приближении принимает значение

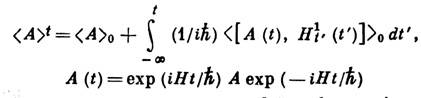
- оператор в представлении Гейзенберга, (. . .)₀ - усреднение с равновесным статистич. оператором. К. ф. можно представить через запаздывающие двухвременные Грина функции

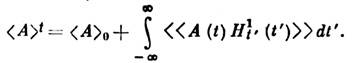
В перем. электрич. поле с частотой 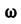получаем К. ф. для тензора электропроводности:

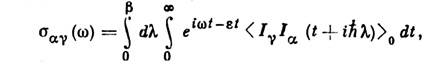
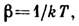I_a - оператор электрич. тока,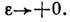

В перем. магн. поле получаем К. ф. для тензора магн. восприимчивости:

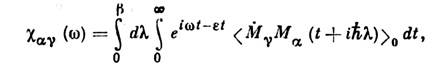
М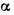- оператор 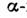компоненты полного магн. момента.

В перем. эл.-магн. поле с частотой w и волновым вектором k получаем К. ф. для диэлектрич. восприимчивости как ф-ции от k,

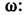
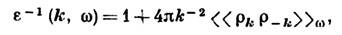
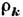- фурье-компоненты оператора плотности заряда, 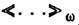- фурье-компоненты запаздывающей двух-временной ф-ции Грина. Неравновесные процессы, к-рые не являются результатом действия внеш. полей, а вызваны термодинамич. неоднородностями в системе (термич. возмущениями), как, напр., вязкость, теплопроводность, диффузия, требуют более радикального изменения описания неравновесного состояния (см. Грина -

Кубо формулы). ц. н. Зубарев.

Физическая энциклопедия. В 5-ти томах. — М.: Советская энциклопедия. Главный редактор А. М. Прохоров. 1988.