- Алгебра А
-
Алгебра А
Базисом предложенной Крисом Дейтом и Хью Дарвеном Алгебры A являются операции реляционного отрицания (дополнения), реляционной конъюнкции (или дизъюнкции) и проекции (удаления атрибута). Реляционные аналоги логических операций определяются в терминах отношений на основе обычных теоретико-множественных операций и позволяют выражать напрямую операции пересечения, декартова произведения, естественного соединения, объединения отношений и так далее. Путем комбинирования базовых операций выражаются операции переименования атрибутов, соединения общего вида, взятия разности отношений. Алгебра A позволяет лучше осознать логические основы реляционной модели, хотя, безусловно, является в меньшей степени ориентированной на практическое применение, чем алгебра Кодда.
Содержание
Обозначения и вводные замечания
r — отношение,
A — имя атрибута отношения r,
T — имя соответствующего типа (то есть типа или домена атрибута A),
v — значение типа T.Тогда:
- заголовком Hr отношения r называется множество атрибутов, то есть упорядоченных пар вида <A, T>. По определению никакие два атрибута в этом множестве не могут содержать одно и то же имя атрибута A;
- кортеж tr, соответствующий заголовку Hr, — это множество упорядоченных триплетов вида <A, T, v>, по одному такому триплету для каждого атрибута в Hr;
- тело Br отношения r — это множество кортежей tr. Заметим, что (в общем случае) могут существовать такие кортежи tr, которые соответствуют Hr, но не входят в Br.
Операции
Операция реляционного дополнения
Пусть s обозначает результат операции <NOT> r.
Тогда:
Операция <NOT> производит дополнение s заданного отношения r. Заголовком s является заголовок r. Тело s включает все кортежи, соответствующие этому заголовку и не входящие в тело r.Операция удаления атрибута
Пусть s обозначает результат операции r <REMOVE> A. Для обеспечения возможности выполнения операции требуется, чтобы существовал некоторый тип (или домен) T такой, что <A, T>
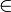 Hr (то есть в состав заголовка отношения r должен входить атрибут A).
Hr (то есть в состав заголовка отношения r должен входить атрибут A).Тогда:
Операция <REMOVE> производит отношение s, формируемое путем удаления указанного атрибута A из заданного отношения r. Операция эквивалентна взятию проекции r на все атрибуты, кроме A. Заголовок s получается теоретико-множественным вычитанием из заголовка r множества из одного элемента {<A, T>}. Тело s состоит из таких кортежей, которые соответствуют заголовку s, причем каждый из них является подмножеством некоторого кортежа тела отношения r.Операция переименования
Пусть s обозначает результат операции r <RENAME> (A, B). Для обеспечения возможности выполнения операции требуется, чтобы существовал некоторый тип T, такой, что <A, T>
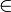 Hr, и чтобы не существовал такой тип T, что <B, T>
Hr, и чтобы не существовал такой тип T, что <B, T> 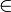 Hr. (Другими словами, в схеме отношения r должен присутствовать атрибут A и не должен присутствовать атрибут B.)
Hr. (Другими словами, в схеме отношения r должен присутствовать атрибут A и не должен присутствовать атрибут B.)Тогда:
В схеме результата B заменяет A;
В кортежах тела результата имя значений атрибута A меняется на B. Операция <RENAME> производит отношение s, которое отличается от заданного отношения r только именем одного его атрибута, которое изменяется с A на B. Заголовок s такой же, как заголовок r, за исключением того, что пара <B, T> заменяет пару <A, T>. Тело s включает все кортежи тела r, но в каждом из этих кортежей триплет <B, T, v> заменяет триплет <A, T, v>.Операция реляционной конъюнкции
Пусть s обозначает результат операции r1 <AND> r2. Для обеспечения возможности выполнения операции требуется, чтобы если <A, T1>
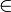 Hr1 и <A, T2>
Hr1 и <A, T2> 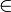 Hr2, то T1 = T2. (Другими словами, если в двух отношениях-операндах имеются одноименные атрибуты, то они должны быть определены на одном и том же типе (домене).)
Hr2, то T1 = T2. (Другими словами, если в двух отношениях-операндах имеются одноименные атрибуты, то они должны быть определены на одном и том же типе (домене).)Тогда:
Заголовок результата получается путем объединения заголовков отношений-операндов, как в операциях TIMES и JOIN в алгебре Кодда;
Кортеж результата определяется как объединение кортежей операндов; поэтому:
если схемы отношений-операндов имеют непустое пересечение, то операция <AND> работает как естественное соединение;
если пересечение схем операндов пусто, то <AND> работает как расширенное декартово произведение;
если схемы отношений полностью совпадают, то результатом операции является пересечение двух отношений-операндов.Операция <AND> является реляционной конъюнкцией, в некоторых случаях выдающей в результате отношение s, ранее называвшееся естественным соединением двух заданных отношений r1 и r2. Заголовок s является объединением заголовков r1 и r2. Тело s включает каждый кортеж, соответствующий заголовку s и являющийся надмножеством некоторого кортежа из тела r1 и некоторого кортежа из тела r2.
Операция реляционной дизъюнкции
Пусть s обозначает результат операции r1 <OR> r2. Для обеспечения возможности выполнения операции требуется, чтобы если <A, T1>
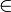 Hr1 и <A, T2>
Hr1 и <A, T2> 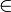 Hr2, то должно быть T1 = T2 (одноименные атрибуты должны быть определены на одном и том же типе).
Hr2, то должно быть T1 = T2 (одноименные атрибуты должны быть определены на одном и том же типе).Тогда:
Из схемы результата удаляются атрибуты-дубликаты;
если у операндов нет общих атрибутов, то в тело результирующего отношения входят все такие кортежи ts, которые являются объединением кортежей tr1 и tr2, соответствующих заголовкам отношений-операндов, и хотя бы один из этих кортежей принадлежит телу одного из операндов; если у операндов имеются общие атрибуты, то в тело результирующего отношения входят все такие кортежи ts, которые являются объединением кортежей tr1 и tr2, соответствующих заголовкам отношений-операндов, если хотя бы один из этих кортежей принадлежит телу одного из операндов, и значения общих атрибутов tr1 и tr2 совпадают;
если же схемы отношений-операндов совпадают, то тело отношения-результата является объединением тел операндов.Операция <OR> является реляционной дизъюнкцией и обобщением того, что ранее называлось объединением. Заголовок s есть объединение заголовков r1 и r2. Тело s состоит из всех кортежей, соответствующих заголовку s и являющихся надмножеством либо некоторого кортежа из тела r1, либо некоторого кортежа из тела r2.
Полнота алгебры A
Алгебра A является полной, то есть на основе введенных операций выражаются все операции алгебры Кодда. Операция <REMOVE> — аналог операции PROJECT. Операция переименования атрибутов <RENAME> — аналог операции RENAME. UNION является частным случаем операции <OR>, TIMES, INTERSECT и NATURAL JOIN — частные случаи операции <AND>. Через операции Алгебры A выражаются операции взятия разности MINUS (если отношения r1 и r2 совместимы по объединению, то r1 MINUS r2 = r1 <AND> <NOT> r2), ограничения (WHERE), соединения общего вида (JOIN) и реляционного деления (DIVIDE BY).
- заголовком Hr отношения r называется множество атрибутов, то есть упорядоченных пар вида <A, T>. По определению никакие два атрибута в этом множестве не могут содержать одно и то же имя атрибута A;
Wikimedia Foundation. 2010.
