ПРИСОЕДИНЕННОЕ ПРЕДСТАВЛЕНИЕ
- ПРИСОЕДИНЕННОЕ ПРЕДСТАВЛЕНИЕ
группы Ли или алгебраической группы G - линейное представление Ad группы Gв касательном пространстве Te(G).(или в алгебре Ли  группы G), сопоставляющее каждому
группы G), сопоставляющее каждому  дифференциал Ad a=d(Int a)e внутреннего автоморфизма Int a:
дифференциал Ad a=d(Int a)e внутреннего автоморфизма Int a:  . Если
. Если  - линейная группа в пространстве V, то
- линейная группа в пространстве V, то

Ядро Кеr Ad содержит центр группы G, а в случае, когда G связна и основное поле имеет характеристику 0, совпадает с центром. Дифференциалом П. п. группы G в точке еслужит присоединенное представление ad алгебры  .
.
Присоединенным представлением алгебры Ли  наз. линейное представление ad алгебры
наз. линейное представление ad алгебры  в модуле
в модуле  , действующее по формуле
, действующее по формуле
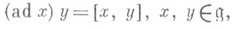
где [ , ] - операция в алгебре  . Ядро Кеr ad есть центр алгебры Ли
. Ядро Кеr ad есть центр алгебры Ли  . Присоединенные операторы ad x являются дифференцированиями алгебры
. Присоединенные операторы ad x являются дифференцированиями алгебры  и наз. внутренними дифференцированиями. Образ ad
и наз. внутренними дифференцированиями. Образ ad  называется присоединенной алгеброй и является идеалом в алгебре Ли Der
называется присоединенной алгеброй и является идеалом в алгебре Ли Der  всех дифференцирований алгебры
всех дифференцирований алгебры  , причем
, причем  есть пространство
есть пространство  1-мерных когомологий алгебры Ли
1-мерных когомологий алгебры Ли  , определяемых П. п. В частности,
, определяемых П. п. В частности,  , если
, если  - полупростая алгебра Ли над полем характеристики 0.
- полупростая алгебра Ли над полем характеристики 0.
Лит.:[1] Джекобсон Н., Алгебры Ли, пер. с англ., М., 1964; [2] Понтрягин Л. С., Непрерывные группы, 3 изд., М., 1973; [3] Серр Ж. - П., Алгебры Ля и группы Ли, пер. с англ, и франц., М., 1969; [4] Хамфри Д ж., Линейные алгебраические группы, пер. с англ., М., 1980.
А. Л. Онищик.
Математическая энциклопедия. — М.: Советская энциклопедия.
И. М. Виноградов.
1977—1985.
Полезное
Смотреть что такое "ПРИСОЕДИНЕННОЕ ПРЕДСТАВЛЕНИЕ" в других словарях:
Присоединенное представление — Присоединённое представление группы Ли Присоединённое представление алгебры Ли … Википедия
Присоединенное представление алгебры Ли — Присоединённое представление алгебры Ли называется линейное представление алгебры в модуле , действующее по формуле где … Википедия
Присоединенное представление группы Ли — Присоединённое представление группы Ли G линейное представление группы G в касательном пространстве TeG (или в алгебре Ли группы G), сопоставляющее каждому элементу дифференциал … Википедия
Присоединенное представление лиевой алгебры — Присоединённое представление алгебры Ли называется линейное представление алгебры в модуле , действующее по формуле где … Википедия
ЛИ РЕДУКТИВНАЯ АЛГЕБРА — конечномерная алгебра Ли над полем kхарактеристики 0, присоединенное представление к рой вполне приводимо. Свойство редуктивности алгебры Ли равносильно любому из следующих свойств: 1) радикал алгебры Ли совпадает с центром 2) , где полупростой… … Математическая энциклопедия
МАКСИМАЛЬНЫЙ ТОР — 1) М. т. линейной алгебраической группы G алгебраическая подгруппа в G, являющаяся алгебраическим тором и не содержащаяся ни в какой большей подгруппе такого типа. Пусть, далее, группа Gсвязна. Объединение всех М. т. группы Gсовпадает с… … Математическая энциклопедия
УНИМОДУЛЯРНАЯ ГРУППА — топологическая группа, левоинвариантная Хаара мера на к рой правоинвариантна или, что равносильно, инвариантна относительно преобразования Группа Ли G унимодулярна тогда и только тогда, когда где Ad присоединенное представление. Для связных групп … Математическая энциклопедия
ОТНОСИТЕЛЬНАЯ СИСТЕМА КОРНЕЙ — связной редуктивной алгебраической группы G, определенной над полем k, система ненулевых весов присоединенного представления максимального k расщепимого тора Sгруппы G в алгебре Ли g этой группы. Сами веса наз. корнями G относительно S. О. с. к … Математическая энциклопедия
ШЕВАЛЛЕ ГРУППА — линейная алгебраич. группа над нек рым полем, связанная с полупростой комплексной алгеброй Ли. Пусть Ли полупростая алгебра над ее подалгебра Картана, система корней алгебры относительно система простых корней, базис Шевалле алгебры его линейная… … Математическая энциклопедия
АЛГЕБРА — часть математики, посвященная изучению алгебраических операций. Исторический очерк. Простейшие алгебраич. операции арифметич. действия над натуральными и положительными рациональными числами встречаются в самых ранних математич. текстах,… … Математическая энциклопедия
 группы G), сопоставляющее каждому
группы G), сопоставляющее каждому  дифференциал Ad a=d(Int a)e внутреннего автоморфизма Int a:
дифференциал Ad a=d(Int a)e внутреннего автоморфизма Int a:  . Если
. Если  - линейная группа в пространстве V, то
- линейная группа в пространстве V, то 
 .
. наз. линейное представление ad алгебры
наз. линейное представление ad алгебры  в модуле
в модуле  , действующее по формуле
, действующее по формуле 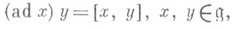
 . Ядро Кеr ad есть центр алгебры Ли
. Ядро Кеr ad есть центр алгебры Ли  . Присоединенные операторы ad x являются дифференцированиями алгебры
. Присоединенные операторы ad x являются дифференцированиями алгебры  и наз. внутренними дифференцированиями. Образ ad
и наз. внутренними дифференцированиями. Образ ad  называется присоединенной алгеброй и является идеалом в алгебре Ли Der
называется присоединенной алгеброй и является идеалом в алгебре Ли Der  всех дифференцирований алгебры
всех дифференцирований алгебры  , причем
, причем  есть пространство
есть пространство  1-мерных когомологий алгебры Ли
1-мерных когомологий алгебры Ли  , определяемых П. п. В частности,
, определяемых П. п. В частности,  , если
, если  - полупростая алгебра Ли над полем характеристики 0.
- полупростая алгебра Ли над полем характеристики 0.