ТЕЙЛОРА РЯД

ТЕЙЛОРА РЯД

- степенной ряд


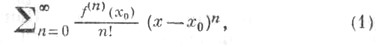
где числовая функция f определена в нек-рой окрестности точки х 0 и имеет в этой точке производные всех порядков. Частными суммами Т. р. являются Тейлора многочлены.
Если х 0 - комплексное число, функция f определена в нек-рой окрестности точки x0 во множестве комплексных чисел и дифференцируема в точке х 0, то существует окрестность этой точки, на к-рой функция f является суммой своего Т. р. (1) (см. Степенной ряд). Если же х 0- действительное число, функция f определена в нек-рой окрестности точки х 0 во множестве действительных чисел и имеет в точке х 0 производные всех порядков, то функция f может ни в какой окрестности точки х 0 не быть суммой своего Т. р. Напр., функция


бесконечно дифференцируема на всей действительной оси, не равна тождественно нулю ни в какой окрестности точки х=0, а все коэффициенты ее Т. р. в этой точке равны нулю.
Если функция раскладывается в нек-рой окрестности данной точки в степенной ряд, то такой ряд единствен и является ее Т. р. в этой точке. Однако один и тот же степенной ряд может являться Т. р. для разных действительных функций. Так, степенной ряд, у к-рого все коэффициенты равны нулю, является как Т. р. функции, тождественно равной нулю на всей действительной оси, так и Т. р. функции (2) в точке x=0.
Достаточным условием сходимости Т. р. (1) к действительной функции f на интервале (х 0-h, х0-h)является ограниченность в совокупности всех ее производных на этом интервале.
Т. р. обобщается на случай отображения подмножеств линейных нормированных пространств в подобные же пространства, в частности на числовые функции нескольких переменных и функции матричного аргумента.
Ряд (1) был опубликован Б. Тейлором (В. Taylor) в 1715; ряд. сводящийся к ряду (1) простым преобразованием, был опубликован И. Бернулли (I. Bernoulli) в 1694.

Лит.:[1] Ильин В. А., Садовничий В. А., С ендов Б. X., Математический анализ, М., 1979; [2] Никольский С. М., Курс матемачического анализа, 3 изд. т. 1, М., 19S3.
Л. Д. Кудрявцев.


Математическая энциклопедия. — М.: Советская энциклопедия. . 1977—1985.

Игры ⚽ Поможем решить контрольную работу

Полезное


Смотреть что такое "ТЕЙЛОРА РЯД" в других словарях:

  • ТЕЙЛОРА РЯД — степенной ряд вида где f(а), f (а), f (а),... значения заданной функции f(х) и ее последовательных производных при х=а (если а=0, то Тейлора ряда называют рядом Маклорена). Частные суммы Тейлора ряда важный аппарат приближенного представления… …   Большой Энциклопедический словарь

  • ТЕЙЛОРА РЯД — степенной ряд, описывающий поведение данной ф ции f( х) в окрестности заданной точки. Точнее, если f(x )в точке х0 имеет бесконечное число производных, то её Т. р. имеет вид Т. р. назван по имени Б. Тейлора (В. Taylor), опубликовавшего ряд (*) в… …   Физическая энциклопедия

  • Тейлора ряд — степенной ряд вида где f(а), f (a), f (а), ...  значения заданной функции f(х) и её последовательных производных при х = а (если а = 0, то ряд Тейлора называют рядом Маклорена). Частные суммы ряда Тейлора  важный аппарат приближённого… …   Энциклопедический словарь

  • Тейлора ряд —         Степенной ряд вида                  , (1)         где f (x) функция, имеющая при х = а производные всех порядков. Во многих практически важных случаях этот ряд сходится к f (x) на некотором интервале с центром в точке а:                   …   Большая советская энциклопедия

  • ТЕЙЛОРА РЯД — степенной ряд вида где f(a), f (a), f (a), ... значения заданной функции Дл:) и её последовательных производных при х = а (если а = 0, то Т. р. наз. рядом Маклорена). Частные суммы Т. р. важный аппарат приближённого представления функции f(x). Т …   Естествознание. Энциклопедический словарь

  • Тейлора ряд — …   Википедия

  • Ряд Тейлора — Ряд Тейлора  разложение функции в бесконечную сумму степенных функций. Ряд назван в честь английского математика Брука Тейлора, хотя ряд Тейлора был известен задолго до публикаций Тейлора  его использовали ещё в XVII веке Грегори, а… …   Википедия

  • Ряд тейлора — разложение функции в бесконечную сумму степенных функций. Ряд назван в честь английского математика Тейлора, хотя ряд Тейлора был известен задолго до публикаций Тейлора его использовали ещё в XVII веке Грегори, а также Ньютон. Ряды Тейлора… …   Википедия

  • Ряд Маклорена — Ряд Тейлора разложение функции в бесконечную сумму степенных функций. Ряд назван в честь английского математика Тейлора, хотя ряд Тейлора был известен задолго до публикаций Тейлора его использовали ещё в XVII веке Грегори, а также Ньютон. Ряды… …   Википедия

  • Ряд Бюрмана — Лагранжа — определяется как разложение голоморфной функции f(z) по степеням другой голоморфной функции w(z) и представляет собой далеко идущее обобщение ряда Тейлора. Пусть f(z) и w(z) голоморфны в окрестности некоторой точки , притом w(a) = 0 и a простой… …   Википедия


Поделиться ссылкой на выделенное

Прямая ссылка:
… Нажмите правой клавишей мыши и выберите «Копировать ссылку»