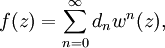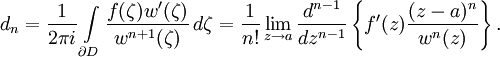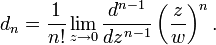- Ряд Бюрмана — Лагранжа
-
Ряд Бюрмана — Лагранжа
Ряд Бюрмана — Лагранжа определяется как разложение голоморфной функции f(z) по степеням другой голоморфной функции w(z) и представляет собой далеко идущее обобщение ряда Тейлора.
Пусть f(z) и w(z) голоморфны в окрестности некоторой точки
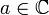 , притом w(a) = 0 и a — простой нуль функции w(z). Теперь выберем некую область
, притом w(a) = 0 и a — простой нуль функции w(z). Теперь выберем некую область 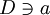 , в которой f и w голоморфны, а w однолистна в
, в которой f и w голоморфны, а w однолистна в 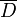 . Тогда имеет место разложение вида:
. Тогда имеет место разложение вида:где коэффициенты dn вычисляются по следующему выражению:
Теорема об обращении рядов
Частным случаем применения рядов является так называемая задача об обращении ряда Тейлора.
Рассмотрим разложение вида
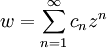 . Попытаемся с помощью полученного выражения вычислить коэффициенты ряда
. Попытаемся с помощью полученного выражения вычислить коэффициенты ряда 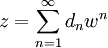 :
:Литература
- Шабат Б. В. Введение в комплексный анализ. — М.: Наука. — 1969, 577 стр.
Wikimedia Foundation. 2010.
Ряд Бюрмана-Лагранжа — определяется как разложение аналитической функции f(z) по степеням другой аналитической функции w(z) и представляет собой далеко идущее обобщение ряда Тейлора. Пусть f(z) и w(z) аналитичны в окрестности некоторой точки , притом w(a) = 0 и a… … Википедия
Ряд Бурмана — Лагранжа — Ряд Бюрмана Лагранжа определяется как разложение аналитической функции f(z) по степеням другой аналитической функции w(z) и представляет собой далеко идущее обобщение ряда Тейлора. Пусть f(z) и w(z) аналитичны в окрестности некоторой точки ,… … Википедия
БЮРМАНА - ЛАГРАНЖА РЯД — ряд Лагранжа, степенной ряд, полностью решающий задачу локального обращения голоморфных функций. Именно, пусть функция комплексного переменного z регулярна в окрестности точки , причем и . Тогда в нек рой окрестности точки плоскости определена… … Математическая энциклопедия
ЛАГРАНЖА РЯД — степенной ряд, дающий решение задачи локального обращения голоморфной функции комплексного переменного. Первоначальное решение задачи обращения, данное Ж. Лагранжем (J. Lagrange, 1770), было затем усовершенствовано А. Бюрманом (H. Burmann, 1779) … Математическая энциклопедия
Теорема Лагранжа об обращении рядов — Эта статья или раздел нуждается в переработке. Пожалуйста, улучшите статью в соответствии с правилами написания статей. Пусть функция … Википедия
СТЕПЕННОЙ РЯД — 1)С. р. по одному комплексному переменному z функциональный ряд вида где a центр ряда, bk его коэффициенты, bk(z a)k члены ряда. Существует число r, называемое радиусом сходимости С. р. (1) и определяемое по формуле Коши Адамара такое, что при |z … Математическая энциклопедия
ОБРАЩЕНИЕ РЯДА — получение по известному степенному ряду ряда для обратной функции в виде где Ряд (2) наз. также О. р. (1), или рядом Лагранжа. Более общая задача о получении разложения произвольной сложной аналнтич. функции F[j(w)]решается Бюрмана Лагранжа рядом … Математическая энциклопедия