СТОХАСТИЧЕСКАЯ АППРОКСИМАЦИЯ

метод решения класса задач статистич. оценивания, в к-ром новое значение оценки представляет собой поправку к уже имеющейся оценке, основанную на новом наблюдении. Первая процедура С. а. была предложена в 1951 X. Роббинсом(Н. Robbins) и С. Монро (S. Мопге).
Пусть каждое измерение Y_n(X_n) функции R(х), 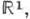в точке Х _n содержит случайную ошибку с нулевым средним. Процедура С. а. Роббинса- Монро для нахождения корня уравнения 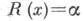имеет вид

Если функция R(x), напр., убывает, |R(х)|растет не быстрее, чем линейная функция, а случайные ошибки независимы, то Х _п стремится к корню х ₀ уравнения с вероятностью 1 и в среднем квадратическом (см. [1], [2]). Из (1) видно, что процедура С. а. рекуррентна, т. е. получение нового значения оценки возможно без запоминания старых измерений Y_n, и удобна, когда неизвестно заранее, в какой момент потребуется представление оценки - она формируется непрерывно на основании наблюдений, имеющихся к данному моменту. Эти черты сближают С. а. с рекуррентными фильтрами и обусловливают популярность С. а. в теоретических и прикладных работах. Процедура (1) непосредственно обобщается на многомерный случай.
Другая процедура С. а., применимая для нахождения точки максимума функции регрессии R(x), принадлежит Дж. Киферу (J. Kiefer) и Дж. Вольфовицу (J. Wolfowitz). Пусть Y_n(x) - наблюдение в точке х. Тогда процедура С. а. Кифера - Вольфовица имеет вид

Доказывается, что Х _п сходится к точке максимума x_max функции R(x), если, напр., R'(x)(x-x_max)<0при функция регрессии и дисперсия случайных ошибок растут не слишком быстро при и выполнены условия

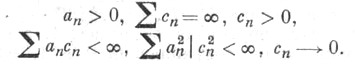
Процедура С. а. Кифера - Вольфовица также допускает многомерное обобщение: вместо правой части в (2) следует подставить приближенное значение градиента функции Y_n(x).
Процедуры С. а. естественным образом обобщаются на непрерывный процесс наблюдений. Напр., если процесс наблюдений возмущается гауссовским белым шумом, то аналог процедуры (1) имеет вид dX(t) = a(t)dY(t). где

- дифференциал наблюдаемого процесса, w(t) -винеровский процесс. Условия сходимости непрерывных процедур аналогичны приведенным выше условиям для дискретного времени (см. [2]). Основным инструментом доказательства сходимости процедур С. а. является теорема о сходимости неотрицательных супермартингалов (см. Мартингал).
Изучалось предельное поведение при соответствующей нормировке разности Х _п -х ₀ при Пусть в (1)

и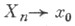 почти наверное при При нек-рых ограничениях, основными из к-рых являются требования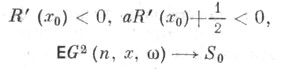

при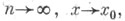 доказывается асимптотич. нормальность с параметрами 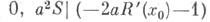величины Наименьшая дисперсия предельного распределения достигается при 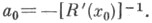Такой выбор аневозможен, т. к. функция R(х)и ее производная неизвестны наблюдателю. Однако в ряде работ построены адаптивные процедуры, в к-рых а=а (п)зависит от наблюдений и приближается к a₀ при 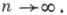Эти процедуры обладают асимптотически оптимальными в смысле асимптотич. дисперсии свойствами.
Результаты об асимптотич. нормальности известны и в многомерном случае. Пусть все корни матрицы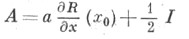

имеют отрицательные действительные части (I - единичная матрица),

при 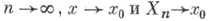почти наверное, и выполнены нек-рые другие не слишком ограничительные условия. Тогда вектор асимптотически нормален с нулевым средним и ковариационной матрицей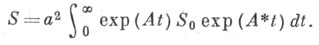

Приведенный выше результат об асимптотически оптимальной процедуре Роббинса - Монро также обобщен на многомерный случай. Доказано, что случайный процесс Z _п сходится к гауссовскому марковскому процессу в логарифмич. масштабе. При нек-рых условиях доказана сходимость моментов случайной величины Х _п к моментам предельного закона.
Процедуры типа С. а. удобны в непараметрич. ситуации, т. к. они применимы при наличии скудной априорной информации о функции регрессии. Однако они применимы и для оценки параметра плотности 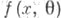по независимым наблюдениям X₁ , . . . , Х _п с этой плотностью. При нек-рых ограничениях рекуррентная процедура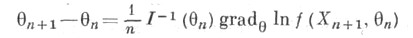

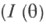- информационная матрица Фишера плотности f) является состоятельной и асимптотически эффективной рекуррентной оценкой параметра Аналогичная процедура возможна и в случае непрерывного времени.
Изучалось поведение процедур С. а. в случае, когда функция регрессии имеет несколько нулей (несколько точек экстремума), различные модификации и обобщения процедур С. а.

Лит.:[1] Вазан М., Стохастическая аппроксимация, пер. с англ., М., 1972; [2] Невельсон М. Б., Xасьминский Р. 3., Стохастическая аппроксимация и рекуррентное оценивание, М., 1972; [3] Цыпкин Я. 3., Адаптация и обучение в автоматических системах, М., 1968; [4] его же, Основы теории обучающих систем, М., 1970.
Р. 3. Хасъминский.