РИМАНОВА ПОВЕРХНОСТЬ

а н а л и т и ч е с к ой ф у н к ц и и w=f(z) к о м п л е к с н о г о п е р ем е н н о г о z - поверхность R такая, что данная полная аналитическая функция w=f(z), вообще говоря многозначная, может рассматриваться как однозначная аналитич. ция w=F(p)точки рповерхности R.

Понятие Р. п. возникло в связи с изучением алгебраич. функций w=f(z), определяемых алгебраич. уравнением

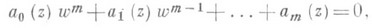(1)

где a_j(z), j=0, ..., т,- многочлены с постоянными коэффициентами, . В работах В. Пюизё (V. Puiseaux, 1850-51) было достигнуто ясное понимание многозначности, присущей этим функциям w=f(z), когда каждому значению переменного zставится в соответствие тзначений переменного w. Б. Риман (В. Riemann, 1851-57, см. [1]) впервые показал, как для любой алгебраич. функции построить поверхность, на к-рой ее можно рассматривать как однозначную рациональную функцию точки. Полученную Р. п. можно отождествить с алгебраич. кривой, определяемой уравнением (1). Вообще, для всего дальнейшего развития теории Р. п., связанного с именами Ф. Клейна(F. Klein), А. Пуанкаре (Н. Poincare), П. Кёбе (Р. Коеbе) и др., характерно (то усиливающееся, то несколько ослабевающее) взаимопроникновение, с одной стороны, идей и методов теории функций комплексного переменного, с другой - алгебры и алгебраич. геометрии. Важной вехой в этом развитии явилось первое издание книги Г. Вейля [18], в к-рой было сформулировано общее понятие абстрактной Р. п.

О п р е д е л е н и е А: связное хаусдорфово топологич. пространство R наз. абстрактной р и м а н о в о й поверхностью, или просто р и м а н о в ой поверхностью, если оно допускает покрытие открытыми множествами Uс соответствующим каждому множеству Uгомеоморфным отображением , где 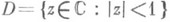есть единичный круг на плоскости 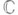комплексного переменного z, причем если точка 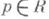принадлежит Uи U', то взаимно однозначное соответствие z'=a'a^-1(z) есть конформное отображение I рода в окрестности точки , то есть z'=a'a^-1(z)есть однолистная аналитич. ция в окрестности точки 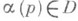. Иначе говоря, абстрактная Р. п. есть двумерное комплексное аналитич. многообразие.

Определение р и м а н о в о й п о в е р х н о с т и с к р а е м отличается от определения А тем, что наряду с гомеоморфизмами допускаются гомеоморфизмы 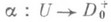, где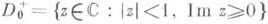

- единичный полукруг на плоскости 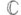, причем обычно предполагается, что не является Р. п. в смысле определения А. Точки Р. п. с краем 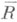, имеющие окрестности, гомеоморфные D, наз. внутренними, а остальные точки, отображающиеся в точки отрезка

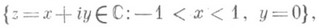
образуют край 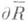. Совокупность внутренние точек 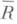(в н у т р е н н о с т ь ) есть Р. п. в смысле определения А. Таким образом, в случае Р. п. с краем обычно край предполагается непустым множеством.

Р. п. (или Р. п. с краем) есть триангулируемое и ориентируемое многообразие со счетной базой, к-рое, следовательно, сепарабельно и метризуемо. Компактная Р. п. (без края) наз. з а м к н у т о й Р. п.; более широкий класс к о н е ч н ы х Р. п. включает замкнутые Р. п. и компактные Р. п. с краем, состоящим из конечного числа связных компонент. Некомпактные Р. п. с краем или без него наз. открытыми Р. п. В нек-рых случаях в определении А более удобно допускать конформное отображение не только I рода, но и II рода. Получающаяся при таком подходе Р. п. с краем (или без него) не является уже, вообще говоря, ориентируемой, но в предположении ее конечности она может быть вложена конформно в ориентируемую замкнутую Р. п.- дубль римановой поверхности (см. [8]).

Пусть аналитич. ция w=f(z) задана одним из своих регулярных элементов ( а, Р)=( а, Р(z-а)), т. е. парой, состоящей из точки и степенного ряда

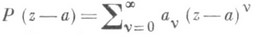
с центром аи радиусом сходимости Аналитическое продолжение элемента (a, P)вдоль всевозможных путей в расширенной плоскости позволяет получить все регулярные элементы такого же типа (b, Q), составляющие в совокупности полную аналитич. цию, к-рую мы будем продолжать обозначать w=f(z). Кроме того, при аналитич. родолжении появляются элементы более общей природы

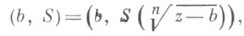
т. е. пары, состоящие из точки 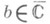и обобщенного степенного ряда (р я д а П ю и з ё):

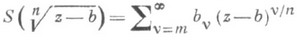
или (в случае, когда 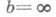- бесконечно удаленная точка):

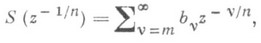
где т - целое, а п- натуральное числа, причем эти ряды сходятся соответственно при или при 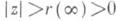. Обобщенные элементы (b, S), а точнее их классы эквивалентности, составляют в совокупности аналитический образ А _f, соответствующий данной аналитич. ции w=f(z). Среди составляющих аналитич. образ классов эквивалентности элементов (b, S)различаются регулярные с n=1 и разветвленные с n>1. Введение подходящей топологии на аналитич. образе A_f превращает его в Р. п. R_f аналитич. функции w=f(z). Это получается, напр., если задавать окрестность элемента 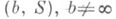, как множество, состоящее из самого элемента (b, S )и всех тех регулярных элементов ( а, Р )из A_f, для к-рых 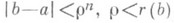и ряд Р(z-а )сходится к одному из попределений ряда в их общей области определения, т. е.

где e - один из корней из единицы степени п,eⁿ=1. Окрестность элемента 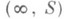состоит из самого элемента 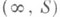и всех тех регулярных элементов ( а, Р )из A_f, для к-рых 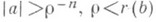и ряд Р(z-a) сходится к одному из попределений ряда S(z^-1/n). Пространство R_f удовлетворяет всем условиям определения А.

Таким образом, каждой аналитич. ции w=f(z)соответствует Р. п. R_f, на к-рой эта функция представляется как однозначная аналитич. ция точки w= F(p), 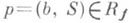. Это означает, что в окрестности любой точки р ₀ - (b, S). существует локальный униформизирующий параметр , через к-рый wвыражается как однозначная аналитич. ция w=P(t)=F(p). Иначе говоря, Р. п. R_f аналитич. функции есть геометрич. конструкция для глобальной униформизации многозначного, вообще говоря, соотношения w=f(z). В окрестности каждой точки 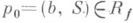оно униформизируется посредством двух однозначных аналитич. ций z=b+tⁿ и w=S(t). С другой стороны, отображение проектирования 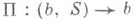, ставящее в соответствие каждому элементу его центр b, показывает, что Р. п. R_f аналитич. функции есть (разветвленная) накрывающая поверхность над расширенной комплексной плоскостью или, что то же, над Римана сферой. Проекции разветвленных элементов (b, S)с n>1 суть точки ветвления этого накрытия.

В то же время каждой априори заданной Р. п. Rсоответствует бесконечно много аналитич. ций w=f(z), для к-рых именно Rявляется их Р. п., R_f=R. Это утверждение для случая замкнутых Р. п. было высказано и обосновано еще Б. Риманом в 1851. Центральным пунктом соответствующего доказательства является конструкция гармонич. функций на R с заданными особенностями. Данное Б. Риманом обоснование опиралось на некритич. применение т. н. Дирихле принципа;строгое доказательство впервые было дано П. Кёбе (1909); позднее были даны более простые доказательства этого фундаментального положения, в том числе и опирающиеся на надлежащим образом применяемый принцип Дирихле (см., напр., [3], [4], [17], [18]).

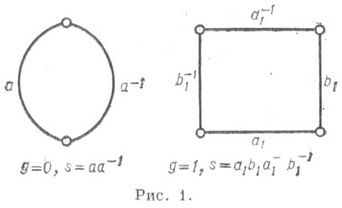
Какова бы ни была ориентируемая топологич. поверхность S, можно построить Р. п. R. гомеоморфную S, т. е. построить Р. п. Rтого же топологич. типа, что и S. Замкнутые Р. н. топологически вполне характеризуются одним числом - родом 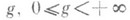. Топологич. тип такой Р. п . R при g=0есть сфера, при g=1 - тор, при g>l - обобщенный тор, или сфера с g ручками. Разрезав Р. п. R рода g=0 вдоль нек-рой дуги, получают в качестве ее топологич. модели, или н о рм а л ь н о й ф о р м ы, двуугольник с символом s=aa^-1, указывающим, что точки сторон аи а ^-1 отождествляются; при необходимо сделать 2g канонических разрезов a_l b₁, ..., a_g, b_g, после чего получается нормальная форма замкнутой P. п. R - многоугольник с 4g сторонами, попарно отождествляемыми, символ s=a₁ ... должен указывать порядок следования сторон. Напр., на рис. 1 изображены нормальные формы сферы при g=0 и тора при g=1 с их символами. С аналитич. точки зрения замкнутая Р. п. Rхарактеризуется тем, что она есть Р. п. нек-рой алгебраич. функции w=f(z), определяемой алгебраич. уравнением (1) степени т. Эту Р. п. Rможно представлять себе также в виде тлистов, про-

стирающихся над сферой Римана и определенным образом соединяющихся между собой в точках ветвления и вдоль нек-рых линий, соединяющих эти точки (способ соединения определяется конкретным видом уравнения (1)). При этом род gР. п. Rвыражается через число листов ти порядки k₁, ..., k_s точек ветвления Римана - Гурвица формулой

Конечные Р. п. топологически вполне характеризуются родом 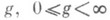, и числом lсвязных компонент края, ; их топологич. типом является сфера с gручками и lотверстиями. В нормальной форме конечной Р. п. число сторон не обязательно четное, нек-рые стороны, соответствующие компонентам края, остаются свободными, не отождествляются. Понятие рода обобщается и для открытых Р. п. R, напр. при помощи исчерпания R последовательностью принадлежащих R компактных Р. п. 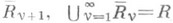с краем таких, что содержится внутри Род g Р. п. R полагают равным , где g_v- род 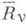. Этот предел существует и не зависит от выбора исчерпания . Однако род не полностью определяет топологич. тип открытой Р. п.; топологич. типы открытых Р. п. могут быть весьма разнообразными. Так, на рис. 2 изображены две модели с g=0 и g=2.

Важной топологич. характеристикой Р. п. Rявляется порядок связности: R наз. о д н о с в я з н о й, если любую простую замкнутую кривую на R можно непрерывно деформировать в точку, не выходя за пределы R, т. е., иначе говоря, если фундаментальная группа поверхности R тривиальна. В противном случае Р. п. R наз. м н о г о с в я з н о й. Важный класс составляют Р. п., п о д о б н ы е о д н о л и с т н ы м: так наз. Р. п.. (с краем или без края), к-рые разделяются любой простой замкнутой кривой на две непересекающиеся части. Напр., на рис. 2, апредставлена топологич. модель многосвязной Р, п., подобной однолистной. Р. п., подобная однолистной, необходимо имеет род нуль. Р. п. R, подобная однолистной, наз. n-с в я з н о й, если минимальное число разрезов, превращающих R в односвязную Р. п., равно 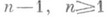(см. рис. 2, б).

Топологич. свойства Р. п. R отнюдь не определяют полностью аналитич. свойства R, т. е. топологич. свойства R не определяют полностью поведение функций различных классов на R. В частности, пусть 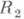- функция на Р. п. R¹ со значениями на другой Р. п. R₂. Функция f наз. аналитической на R₁, если для любой точки , можно найти локальные униформизирующие параметры соответственно t=j(р) в окрестности р ₀ на R₁ и t=y(q)в окрестности q₀ на R₂ такие, что сложная функция

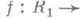
является аналитич. цией комплексного переменного tв окрестности значения t₀=j(p₀). Две Р. п. R₁ и R₂ наз. к о н ф о р м н о э к в и в а л е н т н ы м и, или принадлежащими одному и тому же конформному классу, если существует аналитич. ция , взаимно однозначно отображающая R₁ на R₂. С точки зрения поведения аналитич. ций на Р. п., конформно эквивалентные Р. п. следует рассматривать как одну и ту же Р. п., но топологически эквивалентные Р. п. не всегда являются конформно эквивалентными. Применительно к Р. п. можно следующим образом сформулировать т е о р е м у Р и м а н а о к о нф о р м н о м о т о б р а ж е н и и: всякая односвязная Р. п. R конформно эквивалентна одной из трех областей: 1) расширенной комплексной плоскости 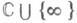, или сфере Римана (эллиптический случай);

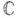2) конечной комплексной плоскости , или сфере Римана с одной выколотой точкой (п а р а б ол и ч е с к и й с л у ч а й); 3) единичному кругу на плоскости , или сфере Римана с разрезом положительной длины (г и п е р б о л и ч ес к и й с л у ч а й). Важный результат состоит в том, что любая Р. п., подобная однолистной, конформно эквивалентна нек-рой канонич. области расширенной комплексной плоскости. В качестве такой канонич. области можно взять всю расширенную плоскость с конечным или бесконечным числом разрезов, параллельных действительной оси, причем нек-рые из этих разрезов могут вырождаться в точки. Как указано выше, в случае од-носвязной Р. п. канонич. область либо не имеет ни одного разреза (э л л и п т и ч е с к и й т и п), либо разрез вырождается в точку (п а р а б о л и ч е с к и й т и п), либо разрез имеет положительную длину (гиперболический тип). Все три типа односвязных Р. п. конформно различны, хотя последние два из них топологически эквивалентны. Проблема т и п а, пока (1983) не получившая полного решения, состоит в разыскании дополнительных условий на односвязную Р. п., при к-рых она принадлежит гиперболическому или параболич. типу (см. [6], [7], [10], [11]).

В общем случае произвольной Р. п. Rодносвязной Р. п. будет всегда ее универсальная накрывающая поверхность 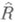, к-рая, следовательно, принадлежит одному из трех указанных типов. Сама Р. п. Rсчитается Р. п. эллиптического, параболического или гиперболического типа в соответствии с тем, какого типа будет ее универсальная накрывающая . Эта классификация Р. п. оправдывается следующими соображениями. Пусть D - одна из трех областей: расширенная комплексная плоскость, конечная комплексная плоскость или единичный круг, а 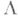- нек-рая группа дробно-линейных отображений области Dна себя (автоморфизмов), не имеющая неподвижных точек в D. Конформное отображение универсальной накрывающей 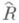на Dпереводит группу 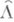преобразований накрытия 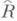, изоморфную фундаментальной группе p₁(R), в нек-рую группу 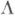автоморфизмов области D. При этом можно рассматривать как конформное отображение факторпространства на факторпространство , а можно отождествить с R. Таким образом, можно рассматривать как конформное отображение Р. п. Rна факторпространство с нек-рой группой автоморфизмов , изоморфной фундаментальной группе p₁(R).

Так как Р. п. R эллиптич. типа обязательно односвязна, то группа тривиальна, а значит, такая Р. п. есть обязательно Р. п. функции, обратной рациональной. Односвязная Р. п. параболич. типа обязательно является Р. п. функции, обратной мероморфной в конечной плоскости. Компактная Р. п. рода g=0, g=1и g>1 является соответственно Р. п. эллиптического, параболического и гиперболич. типа.

В связи с конформной эквивалентностью Р. п. возникает также вопрос о строении группы конформных автоморфизмов Р. п. R. За нек-рыми простыми исключениями эта группа 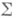дискретна, а для компактных Р. п. рода g>1 она конечна (т е о р е м а Ш в а р ц а). Исключительных случаев, когда группа непрерывна, всего семь, а именно (указаны представители соответствующих конформных классов): сфера в эллиптич. случае; сфера с одной или двумя выколотыми точками и тор в параболич. случае; круг, круг с выколотой точкой и кольцо в гиперболич. случае.

Важное значение имеет также п р о б л е м а модулей Р. п. в различных постановках. Это вопрос о возможном описании разнообразия конформно неэквивалентных Р. п. того или иного вида. Напр., легко устанавливаются следующие положения. Множество видов конформно неэквивалентных двусвязных Р. п., подобных однолистным (колец), зависит от одного действительного параметра (м о д у л я) k,0<k<1; т. <е. два кольца , конформно эквивалентны тогда и только тогда, когда совпадают отношения их радиусов: . Множество видов конформно неэквивалентных n-связных Р. п., подобных однолистным, при n>2 зависит от 3n - 6 действительных параметров. Множество видов конформно неэквивалентных замкнутых Р. п. рода при g=1зависит от двух действительных параметров, а при g>1 - от 6g- 6 действительных параметров (см. Римановых поверхностей конформные классы, а также [3], [12], [13], [15], [16]; относительно поведения функций других классов на Р. п. см. Римановых поверхностей классификация).

Важным аспектом теории Р. п. является связь с понятием униформизации. Для многозначной, вообще говоря, аналитич. ции

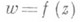(2)

ее Р. п. R_f дает геометрич. средство униформизации: многозначное соотношение (2) заменяется двумя однозначными представлениями:

(3)

выражающими переменные и 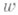однозначно во всей области существования функции (2) как полной аналитич. ции. С другой стороны, подход К. Вейерштрасса (К. Weierstrass) к построению понятия полной аналитич. ции (2) состоит в использовании локального униформизирующего параметра t, позволяющего выразить переменные и аналитически в виде однозначных аналитич. ци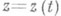й и 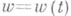локально в окрестности нек-рой точки 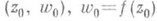. Задача униформизации в ее простейшей классич. постановке есть задача синтеза этих двух идей. Требуется заменить соотношение (2) во всей области его определения двумя аналитич. редставлениями , где t - униформизирующее комплексное переменное, изменяющееся в нек-рой области на плоскости.

Возможность униформизации в указанной постановке установлена П. Кёбе и независимо А. Пуанкаре почти одновременно в 1907. Если Р. п. R_f функции (2) односвязна или подобна однолистной, то задача униформизации сводится к построению конформного отображения Р. п. R_f на плоскую область D. Представления (3) тогда дают искомую униформизацию:

Конформное отображение f на плоскую область существует для Р. п. R_f, подобных однолистным, и только для них (о б щ а я т е о р е м а у н и ф о р м из а ц и и).

В общем случае произвольного аналитич. соотношения (2) Р. п. R_f не является подобной однолистной, но ее универсальная накрывающая односвязна, и следовательно, существует конформное отображение

где D - одна из упоминавшихся областей: 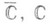или единичный круг. Функция мероморфна на Р. п. R_f, а следовательно и на , причем она зависит только от проекции , точки . Таким образом, получается геометрич. униформизация в виде

а отсюда и аналитич. иформизация:

где и выражаются как мероморфные функции Ф (t)и Y (t)переменного . Эти функции Ф (t)и Y (t)суть автоморфные функции в области Dотносительно группы автоморфизмов , изоморфной фундаментальной группе p₁ (R_f )Р. п. R_f униформизируемой функции (см. [3], [7], [15],[16]).

Лит.:[1] Р и м а н Б., Соч., пер. с нем., М.-Л., 1948; [2] М а р к у ш е в и ч А. И., Теория аналитических функций, 2 изд., т. 1 - 2, М., 1967-68; [3] Г у р в и ц А., К у р а н т Р., Теория функций, пер. с нем., М., 1968; [4] С т о и л о в С., Теория функций комплексного переменного, пер. с рум., т. 1-2, М., 1962; [5] е г о ж е, Лекции о топологических принципах теории аналитических функций, пер. с франц., М., 1964; [6] С п р и н г е р Д ж., Введение в теорию римановых поверхностей, пер. с англ., М., 1960; [7] .Н е в а н л и н н а Р., Униформизация, пер. с нем., М.. 1955; [8] Ш и ф ф е р М., С п е н с е р Д. К., Функционалы на конечных римановых поверхностях, пер. с англ., М., 1957; [9] Ч е б о т а р е в Н. Г., Теория алгебраических функций, М.-Л., 1948; [10] В о л к о в ы с к и й Л. И., "Тр. Матем. ин-та АН СССР", 1950, т. 34, с. 3-171; [11] е г о ж е, "Успехи матем. наук", 1956, т. 11, в. 5, с. 77-84; [12] К р у ш к а л ь С. Л., Квазиконформные отображения и римановы поверхности, Новосиб., 1975; [13] К р у ш к а л ь С. Л., А п а н а с о в Б. Н., Г у с е в с к и й Н. А., Клейновы группы в примерах и задачах, Новосиб., 1978; [14] Итоги науки и техники. Алгебра. Топология. Геометрия, т. 16, М., 1978, с. 191-245; [15] А л ь ф о р с Л., Б е р с Л., Пространства римановых поверхностей и квазиконформные отображения, пер. с англ., М., 1961; [16] Б е р с Л., "Успехи матем. наук", 1973, т. 28, в. 4, с. 153-98; 1974, т. 29, в. 2, с. 86 - 102; [17] K l e i n F., Riemannsche Flachen... Vorlesung von F. Klein, Gott., 1894; [18] W e y l H., Die Idee der Riemannschen Flache, 3 Aufl., Stuttg., 1955; [19] A h 1 f о r s L., S а r i о L., Riemann surfaces, Princeton, I960; [20] P f l u g e r A., Theorie der Riemannschen Flachen, В.- [u. a.], 1957; [21] S a r i о L., N a k a i M., Classification theory of Riemann surfaces, B.- [u. a.], 1970; [22] H e i n s M., Hardy classes on Riemann surfaces, В.- [u. a.], 1969; [23] G u n n i n g R. C., Lectures on Riemann surfaces, Princeton, 1966; [24] е г о ж е, Lectures on Riemann surfaces, Jacobi varieties, Princeton, 1972; [25] Ф о р с т е р О., Римановы поверхности, пер. с нем., М., 1980.

Е. Д. Соломенцев.