- РИМАНОВА ГЕОМЕТРИЯ
- теория риманова пространства. Р и м а н о в ы м п р о с т р а н с т в о м наз. n-мерное связное дифференцируемое многообразие М п, на к-ром задано дифференцируемое поле ковариантного, симметрического и положительно определенного тензора gранга 2. Тензор gназ. м е т р и ч ес к и м т е н з о р о м. Р. г. есть многомерное обобщение внутренней геометрии двухмерных поверхностей в эвклидовом пространстве Е 3. Метрика риманова пространства с точностью до первого порядка малости, по сравнению с размерами рассматриваемой области, совпадает с евклидовой метрикой. Отличие этих метрик оценивается (локально) римановой кривизной - многомерным обобщением понятия гауссовой кривизны поверхности в Е 3.
В основании Р. г. лежат три идеи. Первая идея - осознание факта существования неевклидовой геометрии - геометрии Н. И. Лобачевского. Вторая идея - понятие внутренней геометрии поверхностей, созданной К. Гауссом (С. Gauss). Третья идея - понятие n-мерного пространства, разработанное в 1-й пол. 19 в. Б. Риман (В. Riemann) соединил и обобщил эти идеи в лекции "О гипотезах, лежащих в основании геометрии". Понятия Р. г. сыграли важную роль в создании А. Эйнштейном (A. Einstein) общей теории относительности, дальнейшее ее развитие связано с созданием аппарата тензорного исчисления. Р. г. и ее многочисленные обобщения успешно развиваются, особенно в той ее части, к-рая наз. римановой геометрией в целом, и находят обширные и глубокие механические и физич. применения.
Основные понятия Р. г. следующие.
С к а л я р н о е п р о и з в е д е н и е. В каждом касательном пространстве
 , тензор gопределяет скалярное (внутреннее) произведение
, тензор gопределяет скалярное (внутреннее) произведение  по формуле
по формуле

Верно и обратное: если для любого
 в
в 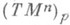 определено скалярное произведение, дифференцируемо зависящее от р, то оно определяет тензорное поле gсуказанными выше свойствами. Степени гладкости М n и gварьируются в зависимости от поставленной задачи. В большинстве случаев достаточно потребовать, чтобы М n было трижды непрерывно дифференцируемо, а поле тензора g - дважды непрерывно дифференцируемо (далее необходимая степень гладкости указываться не будет). В локальных координатах { х i}слокальным базисом
определено скалярное произведение, дифференцируемо зависящее от р, то оно определяет тензорное поле gсуказанными выше свойствами. Степени гладкости М n и gварьируются в зависимости от поставленной задачи. В большинстве случаев достаточно потребовать, чтобы М n было трижды непрерывно дифференцируемо, а поле тензора g - дважды непрерывно дифференцируемо (далее необходимая степень гладкости указываться не будет). В локальных координатах { х i}слокальным базисом 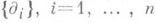 , компоненты тензора gимеют вид
, компоненты тензора gимеют вид

так что

где

Р и м а н о в о п р о с т р а н с т в о к а к м е т р и ч е с к о е п р о с т р а н с т в о. Д л и н а lгладкой кривой
 определяется формулой
определяется формулой

где
 - касательный вектор к c(t). Длина кусочно гладкой кривой равна сумме длин ее гладких звеньев. Если х i = х i(t)- уравнения c(t)в локальных координатах, то
- касательный вектор к c(t). Длина кусочно гладкой кривой равна сумме длин ее гладких звеньев. Если х i = х i(t)- уравнения c(t)в локальных координатах, то

Имея в виду эту формулу, метрику на М n записывают в традиционной форме

и ds наз. элементом длины, а функции gij(x) - коэффициентами метрической (основной, первой квадратичной) формы. У г о л между двумя кривыми в точке их пересечения определяется как угол между касательными к ним. Объём
 области
области  , принадлежащей координатной окрестности, определяется формулой
, принадлежащей координатной окрестности, определяется формулой

где
 . Объем произвольной области равен сумме объемов ее частей, причем каждая из частей лежит в нек-рой координатной окрестности.
. Объем произвольной области равен сумме объемов ее частей, причем каждая из частей лежит в нек-рой координатной окрестности.
Р а с с т о я н и е r( р, q )между точками
 определяется как точная нижняя грань длин всех кусочно гладких кривых, соединяющих
определяется как точная нижняя грань длин всех кусочно гладких кривых, соединяющих  с
с 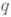 . Аналогично определяется метрика
. Аналогично определяется метрика  в произвольной связной области U. Два римановых пространства
в произвольной связной области U. Два римановых пространства 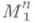 и
и  наз. и з о м е т р и ч н ы м и, если существует отображение
наз. и з о м е т р и ч н ы м и, если существует отображение  , при к-ром
, при к-ром

или, что то же,
 , где с - произвольная кривая в
, где с - произвольная кривая в  . Если j - изометрия, то для любой точки
. Если j - изометрия, то для любой точки  существует координатная окрестность
существует координатная окрестность  и координатная окрестность
и координатная окрестность  такие, что
такие, что 

 . Изометрич. отображение М n на себя наз. д в и ж е н и е м.
. Изометрич. отображение М n на себя наз. д в и ж е н и е м.
Кривая с концами в точках
 и
и 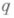 наз. к р а т ч а й ш е й, если ее длина равна
наз. к р а т ч а й ш е й, если ее длина равна  . Стационарная кривая функционала длины lназ. г е о д е з и ч е с к о й линией. Каждая кратчайшая в М n есть геодезическая, и каждая достаточно малая дуга геодезической есть кратчайшая. Область
. Стационарная кривая функционала длины lназ. г е о д е з и ч е с к о й линией. Каждая кратчайшая в М n есть геодезическая, и каждая достаточно малая дуга геодезической есть кратчайшая. Область 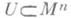 наз. г е о д е з и ч е с к и в ы п у к л о й, если кратчайшие, определенные по метрике
наз. г е о д е з и ч е с к и в ы п у к л о й, если кратчайшие, определенные по метрике  , есть геодезические М n. Если xi = xi(t), i=l, ..., п,- уравнения геодезической в локальной системе координат { хi}, то функции xi(t) удовлетворяют системе уравнений, к-рая в случае, когда t - параметр, пропорциональный длине дуги, имеет вид
, есть геодезические М n. Если xi = xi(t), i=l, ..., п,- уравнения геодезической в локальной системе координат { хi}, то функции xi(t) удовлетворяют системе уравнений, к-рая в случае, когда t - параметр, пропорциональный длине дуги, имеет вид

где

- символы Кристоффеля, gab - элементы матрицы, обратной к

Риманово пространство наз. п о л н ы м (г е о д ез и ч е с к и п о л н ы м), если оно полно как метрич. пространство (если любую дугу геодезической можно неограниченно продолжить в обе стороны). Риманово пространство полно тогда и только тогда, когда оно геодезически полно. В полном римановом пространстве любые две точки можно соединить кратчайшей (не обязательно единственной). На любом дифференцируемом многообразии можно ввести структуру полного риманова пространства.
Р и м а н о в о п р о с т р а н с т в о к а к м н о г оо б р а з и е с о с в я з н о с т ь ю. Ковариантная производная
 наз. с и м м е т р и ч е с к о й и с о вм е с т н о й с м е т р и к о й gпространства М п, если выполняются условия симметричности
наз. с и м м е т р и ч е с к о й и с о вм е с т н о й с м е т р и к о й gпространства М п, если выполняются условия симметричности

и совместности

где X, Y, Z - дифференцируемые векторные поля, а [X, Y] - их коммутатор. Этими условиями производная
 определяется однозначно через поле метрич. тензора g. В локальных координатах { х i}компоненты связности
определяется однозначно через поле метрич. тензора g. В локальных координатах { х i}компоненты связности 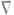 имеют вид
имеют вид 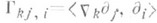 и совпадают с символом Кристоффеля 1-го рода, а
и совпадают с символом Кристоффеля 1-го рода, а
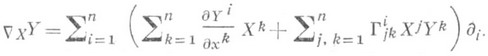
Аналогичной формулой определяется ковариантная производная любого тензора.
Векторное поле Y(t)вдоль кривой c(t)наз. п а р а лл е л ь н ы м, если
 . Аналитически параллельное поле Y(t)определяется решением системы
. Аналитически параллельное поле Y(t)определяется решением системы
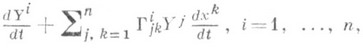
где xi = xi(t) - уравнения кривой c(t). Решения этой системы при различных начальных условиях дают отображение
 в
в  ; оно оказывается изометричным и наз. п а р а л л е л ь н ы м п е р е н ес е н и е м Л е в и - Ч и в и т а. Результат перенесения зависит, вообще говоря, не только от конечных точек с(0) и с(1), но и от самого пути c(t). Кривая, для к-рой
; оно оказывается изометричным и наз. п а р а л л е л ь н ы м п е р е н ес е н и е м Л е в и - Ч и в и т а. Результат перенесения зависит, вообще говоря, не только от конечных точек с(0) и с(1), но и от самого пути c(t). Кривая, для к-рой  , является геодезической, и это свойство геодезической можно взять за ее определение.
, является геодезической, и это свойство геодезической можно взять за ее определение.
П о д м н о г о о б р а з и я р и м а н о в а п р о с тр а н с т в а. Если
 , - дифференцируемое подмногообразие риманова пространства М п, то в каждом касательном пространстве к
, - дифференцируемое подмногообразие риманова пространства М п, то в каждом касательном пространстве к  индуцируется скалярное произведение и тем самым на
индуцируется скалярное произведение и тем самым на  возникает структура риманова пространства с метрич. тензором а, компоненты к-рого вычисляются по формулам
возникает структура риманова пространства с метрич. тензором а, компоненты к-рого вычисляются по формулам 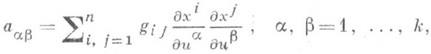
где
 - уравнения
- уравнения 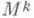 в локальных координатах. Внешняя геометрия
в локальных координатах. Внешняя геометрия  , описывается вторыми квадратичными формами
, описывается вторыми квадратичными формами  , к-рые определяются для каждой единичной нормали vp к
, к-рые определяются для каждой единичной нормали vp к  формулой
формулой
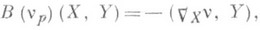
где Xи Y - векторные поля на
 , а
, а  - произвольное поле единичных нормалей, содержащее vp. Для любой формы
- произвольное поле единичных нормалей, содержащее vp. Для любой формы  определяются нормальные кривизны, главные направления и кривизны, средняя и полная кривизны и т. д. и выводятся уравнения Гаусса - Ко-дацци - Риччи, связывающие коэффициенты первой и вторых квадратичных форм. Свойствами вторых форм характеризуются важные классы подмногообразий, напр. минимальные, вполне геодезические, выпуклые и т. п. Для
определяются нормальные кривизны, главные направления и кривизны, средняя и полная кривизны и т. д. и выводятся уравнения Гаусса - Ко-дацци - Риччи, связывающие коэффициенты первой и вторых квадратичных форм. Свойствами вторых форм характеризуются важные классы подмногообразий, напр. минимальные, вполне геодезические, выпуклые и т. п. Для  (гладкая кривая) строится теория, аналогичная теории кривых в Е п, определяются первая, вторая и т. д. кривизны и выводятся уравнения, аналогичные формулам Френе. Первая кривизна кривой k1. обычно наз. геодезической кривизной и вычисляется по формуле
(гладкая кривая) строится теория, аналогичная теории кривых в Е п, определяются первая, вторая и т. д. кривизны и выводятся уравнения, аналогичные формулам Френе. Первая кривизна кривой k1. обычно наз. геодезической кривизной и вычисляется по формуле

если t - длина дуги; в локальных координатах
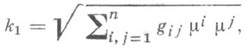
где

a xi=xi(t) - уравнения c(t).
Большой круг задач Р. г. связан с изометрическими погружениями одного риманова пространства в другое и изучением свойств этих погружений. Эти задачи трудны и исследованы мало (более подробно - в двумерном случае).
Э к с п о н е н ц и а л ь н о е о т о б р а ж е н и е
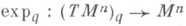 определяется условием: expqX=r, где r - конец дуги геодезической с началом в q, с направлением
определяется условием: expqX=r, где r - конец дуги геодезической с началом в q, с направлением  и длины
и длины 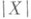 . Если в окрестности точки рввести систему координат, сопоставляя точке рдекартовы координаты точки
. Если в окрестности точки рввести систему координат, сопоставляя точке рдекартовы координаты точки  , то окажется
, то окажется
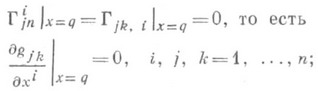
это - т. н. (римановы) н о р м а л ь н ы е координаты.
К р и в и з н а. Если в окрестности точки qввести нормальные координаты, то компоненты метрич. тензора записываются в виде
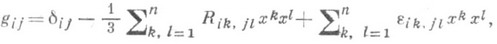
где
 при
при  . Отсюда выводится важное свойство римановой метрики: для любой точки
. Отсюда выводится важное свойство римановой метрики: для любой точки  экспоненциальное отображение
экспоненциальное отображение 
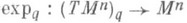 обладает свойством
обладает свойством

где
 при
при  . Добиться более высокого по порядку малости совпадения метрик М п и ( ТМ n)q за счет удачного выбора отображения j в общем случае невозможно. Поэтому коэффициенты
. Добиться более высокого по порядку малости совпадения метрик М п и ( ТМ n)q за счет удачного выбора отображения j в общем случае невозможно. Поэтому коэффициенты  характеризуют отличие метрики М n от евклидовой метрики ( ТМ n)q. Эти коэффициенты являются компонентами т. н. т е н з о р а к р и в и з н ы, или т е н з о р а Р и м а н а - К р и с т о ф ф е л я (в точке q). В локальных координатах { х i}они выражаются через коэффициенты метрич. тензора и их первые и вторые производные по формуле
характеризуют отличие метрики М n от евклидовой метрики ( ТМ n)q. Эти коэффициенты являются компонентами т. н. т е н з о р а к р и в и з н ы, или т е н з о р а Р и м а н а - К р и с т о ф ф е л я (в точке q). В локальных координатах { х i}они выражаются через коэффициенты метрич. тензора и их первые и вторые производные по формуле

С тензором кривизны связан целый ряд других понятий, также (с разных сторон) характеризующих меру отличия метрики М n от евклидовой. Так, через тензор кривизны определяются т е н з о р ы Р и ч ч и

и Э й н ш т е й н а

где
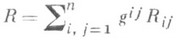
- т. н. с к а л я р н а я к р и в и з н а М n.
Трилинейное отображение, сопоставляющее трем векторным полям X, Y, Z поле

наз. п р е о б р а з о в а н и е м кривизны. Его свойства:
1)
 ;
;
2)
 (тождество Риччи);
(тождество Риччи);
3)
 ;
;
4)
 Кроме того, имеет место т о ж д е с т в о Б и а н к и
Кроме того, имеет место т о ж д е с т в о Б и а н к и

Преобразование кривизны можно связать нек-рой конструкцией с параллельным перенесением. Алгебраич. свойства тензора кривизны выводятся из свойств преобразования кривизны, т. к. через него, а именно через "биквадратичную форму"
 , тензор кривизны (точнее, его значения на векторах X, Y, Z, W )однозначно (алгебраически) выражается (см. Кривизна).
, тензор кривизны (точнее, его значения на векторах X, Y, Z, W )однозначно (алгебраически) выражается (см. Кривизна).
С е к ц и о н н а я к р и в и з н а. Пусть F2 - двумерная поверхность в М n, проходящая через р,s=(TF2)p, Г - простая замкнутая кривая на Г 2, проходящая через р, S - площадь области на F2, ограниченной кривой
 - вектор, полученный из z параллельным перенесением вдоль Г, j - угол между вектором z и касательной составляющей вектора
- вектор, полученный из z параллельным перенесением вдоль Г, j - угол между вектором z и касательной составляющей вектора  Тогда при стягивании Г к точке рсуществует предел
Тогда при стягивании Г к точке рсуществует предел  , к-рый наз. римановой секционной к р и в и з н о й пространства М n в данной точке ри в данном двумерном направлении s (K( р,s). не зависит от поверхности F2,aзависит только от s). Секционная кривизна показывает меру "искривления" М n в данной точке и в данном двумерном направлении. Вообще говоря, в разных двумерных направлениях это искривление различно; но если в каждой точке кривизна K( р,s) не зависит от выбора s, то она не меняется и от точки к точке (т е о р е м а Ш у р а). Тождественное обращение секционной кривизны в нуль - необходимое и достаточное условие того, чтобы М n было локально изометрично En (в целом оно может отличаться от Е п). Секционную кривизну М n можно связать и с другими объектами Р. г., напр.. с дефектом (избытком) геодезич. треугольника (см. Гаусса - Бoннe теорема). Сам Б. Риман определял секционную кривизну как гауссову кривизну двумерной поверхности ехр ps, вычисленную по формуле Гаусса в точке р. В свою очередь, по секционной кривизне метрика М п определяется однозначно в следующем смысле: если у двух многообразий
, к-рый наз. римановой секционной к р и в и з н о й пространства М n в данной точке ри в данном двумерном направлении s (K( р,s). не зависит от поверхности F2,aзависит только от s). Секционная кривизна показывает меру "искривления" М n в данной точке и в данном двумерном направлении. Вообще говоря, в разных двумерных направлениях это искривление различно; но если в каждой точке кривизна K( р,s) не зависит от выбора s, то она не меняется и от точки к точке (т е о р е м а Ш у р а). Тождественное обращение секционной кривизны в нуль - необходимое и достаточное условие того, чтобы М n было локально изометрично En (в целом оно может отличаться от Е п). Секционную кривизну М n можно связать и с другими объектами Р. г., напр.. с дефектом (избытком) геодезич. треугольника (см. Гаусса - Бoннe теорема). Сам Б. Риман определял секционную кривизну как гауссову кривизну двумерной поверхности ехр ps, вычисленную по формуле Гаусса в точке р. В свою очередь, по секционной кривизне метрика М п определяется однозначно в следующем смысле: если у двух многообразий  и
и  секционные кривизны постоянны и равны одному и тому же числу а, то
секционные кривизны постоянны и равны одному и тому же числу а, то  и
и  локально изометричны, если они к тому же оба односвяяны, то - просто изометричны. Односвязное риманово пространство постоянной секционной кривизны аизометрично:
локально изометричны, если они к тому же оба односвяяны, то - просто изометричны. Односвязное риманово пространство постоянной секционной кривизны аизометрично:
n-мерному пространству Лобачевского Ln при a<0; п- мерному евклидову пространству Е п при a=0; n-мерной сфере Sn в Е п +1 радиуса
 при a>0. В общем случае известен следующий результат. Если
при a>0. В общем случае известен следующий результат. Если  - аналитическое риманово пространство непостоянной секционной кривизны и существует диффеоморфизм
- аналитическое риманово пространство непостоянной секционной кривизны и существует диффеоморфизм  , при к-ром
, при к-ром  , то при
, то при  отображение j - изометрия; в случае n=3 это утверждение доказано при нек-рых дополнительных предположениях, а в случае п=2теорема не верна. Однако неизвестно (1983), кроме двумерного случая, какова должна быть функция K( р,s), чтобы для нее существовала метрика g, для к-рой K ( р,s) была бы секционной кривизной. В этом направлении известны только нек-рые отрицательные результаты.
отображение j - изометрия; в случае n=3 это утверждение доказано при нек-рых дополнительных предположениях, а в случае п=2теорема не верна. Однако неизвестно (1983), кроме двумерного случая, какова должна быть функция K( р,s), чтобы для нее существовала метрика g, для к-рой K ( р,s) была бы секционной кривизной. В этом направлении известны только нек-рые отрицательные результаты.
Секционная кривизна связана с преобразованием кривизны
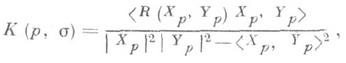 формулой
формулой
а через компоненты тензора кривизны выражается так:

где s определено векторами
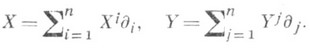
Значение тензора Риччи Rij на векторе Xсвязано с секционной кривизной следующим образом: пусть векторы X, Y1,... , Yn_1 образуют ортонормированный базис в ( ТМ n) р, тогда

где
 - двумерное направление векторов Xи
- двумерное направление векторов Xи 
К л а с с ы р и м а н о в ы х п р о с т р а н с т в. Помимо общих (произвольных) римановых пространств существуют римановы пространства, на к-рых могут быть введены дополнительные структуры. Эти структуры возникают тогда, когда непосредственно на метрику или на кривизну накладываются те или иные условия геометрического или алгебраич. характера. Таким способом определяются важные классы римановых пространств: многообразия постоянной секционной кривизны (см. Пространственные формы), однородное пространство, симметрическое пространство, эрмитовы и кэлеровы многообразия, пространства Эйнштейна и т. д.
О б о б щ е н и я. Развитие идей Р. г. и геометрии в целом привело к ряду обобщений понятия Р. г.
П с е в д о р и м а н о в а г е о м е т р и я - теория псевдориманова пространства. Псевдоримановым пространством наз. дифференцируемое многообразие, на к-ром задано поле знакопеременного симметричного невырожденного тензора.
Ф и н с л е р о в а г е о м е т р и я - теория дифференцируемого многообразия, на касательном расслоении к-рого задана функция F(x,l), однородная первой степени по l. Длина lкривой с(t)вычисляется:

П р о с т р а н с т в а о г р а н и ч е н н о й к р и в и з н ы - теория двумерных метрич. многообразий с внутренней метрикой (без всяких предположений гладкости), в к-рых определена интегральная кривизна любого ограниченного борелевского множества. Сюда, в частности, относится внутренняя геометрия выпуклых поверхностей. Этот класс метрич. пространства можно получить, присоединяя к двумерным римановым пространствам двумерные метризованные многообразия, метрика к-рых в окрестности каждой точки допускает равномерное приближение римановыми метриками с ограниченными в совокупности интегралами от абсолютной гауссовой кривизны.
П р о с т р а н с т в а к р и в и з н ы н е б о л ь ш е K - теория полных метрич. многообразий с внутренней метрикой, в к-рых сумма верхних углов треугольников, составленных из кратчайших, не превосходит суммы углов треугольника на плоскости постоянной кривизны K с такими же длинами сторон (кроме того, предполагается, что любые две точки можно соединить единственной кратчайшей).
См. также Геодезических геометрия, Конформная геометрия, Риманово пространство обобщенное.
Лит.:[1] Р и м а н Б., Соч., пер. с нем., М.-Л., 1948; [2] Р а ш е в с к и й П. К., Риманова геометрия и тензорный анализ, 3 изд., М., 1967; [3] Э й з е н х а р т Л. П., Риманова геометрия, пер. с англ., М., 1948; [4] Г р о м о л Д., К л и н г е н б е р г В., М е й е р В., Риманова геометрия в целом, пер. с нем., М., 1971: [5] А л е к с а н д р о в А. Д., Внутренняя геометрия выпуклых поверхностей, М.-Л., 1948; [6] Б у р а г о Ю. Д., 3 а л г а л л е р В. А., "Успехи матем. наук" 1977, т. 32, в. 3, с. 3-55; [7] М и л н о р Д ж., Теория Морса пер. с англ., М., 1965; [8] К а р т а н Э., Геометрия риманоиых пространств, пер. с франц., М.-Л., 1936; [9] К u I k а r n i R. S. "Ann. Math.", 1970, v. 91, № 2, p. 311 - 31; [10] W о 1 f J. A., Spaces of constant curvature, N. Y., 1967. В. А. Топоногов
Математическая энциклопедия. — М.: Советская энциклопедия. И. М. Виноградов. 1977—1985.
