РИМАНОВА ПОВЕРХНОСТЬ

РИМАНОВА ПОВЕРХНОСТЬ

- поверхность, локально устроеннаякак область комплексной плоскости (комплексное аналитич. многообразие). Если X - нек-рая поверхность(многообразие), представимая в виде объединения открытых подмножеств {U_i}, каждоеиз к-рых эквивалентно нек-рой области в , тоговорят, что на X задана структура Р. п. Др. словами, существуют ф-ции f_i,непрерывно и взаимно однозначно отображающие на U_i, причём для любой пары индексов i и j ф-ции перехода являются аналитическими функциями, взаимно однозначно отображающими на . Пара наз. картой, а совокупность всех карт, покрывающих X, - атласом. <Ниже приведены примеры Р. п.

1. Всякая область в являетсяР. п. При этом атлас можно выбрать состоящим из одной карты, положив и /, равной тождеств. отображению.

2. Расширенная комплексная плоскость (сфера Р и м а н а),получающаяся добавлением к бесконечно удалённой точки, является Р. п. В этом случае атлас можно выбратьсостоящим из двух карт, положив, напр.,

Ф-ция f₁ отображает круг на себя, а ф-ция f₂ отображает внешность единичного кругана единичный круг. При этом бесконечно удалённая точка переходит в нуль.

3. Р. п. аналитич. ф-ции. Если ф-ция f(z), первоначально заданнаяв нек-рой окрестности точки z₀, допускает аналитическое продолжение вдольк.-л. замкнутого контура, причём в результате этого продолжения получаетсяф-ция с др. значениями в окрестности z₀, то точку z₀ до обхода этого контура и ту же точку после его обхода естественно считатьразл. точками. Проводя эту процедуру со всеми точками первонач. областиопределения ф-ции, получаем в результате неоднолистную область, имеющуюструктуру Р. п. и называемую Р. п. ф-ции f(z). При обходе вдольконтура описанного выше типа говорят о переходе Р. п. на другой лист. Р. <п. аналитич. ф-ций позволяет рассматривать многозначные функции в как однозначные ф-ции на своих Р. п.

4. Пусть - нек-рая область в и Г - нек-рая группа взаимно однозначных аналитич. отображений в себя, причём совокупность точек, получающихся из при действии Г, образует дискретное множество в .Отождествляя точки ,переходящие друг в друга при преобразованиях из Г, можно определить поверхность(многообразие), к-рая имеет структуру Р. п. и обозначается .Напр., преобразования 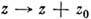, где z₀ - фиксиров. число, приводят к поверхности, топологическиэквивалентной цилиндру.

Согласно теореме об униформизации, любая связная Р. п. эквивалентналибо ,либо ,либо , где - верхняя полуплоскость. Др. словами, существует аналитич. ф-ция, взаимнооднозначно отображающая связную Р. п. на одну из перечисленных.

Р. п. применяют в разл. областях теоретич. и матем. физики. В частности, <в квантовой теории поля часто изучаемые величины (амплитуды рассеяния, <формфакторы и т. д.) являются многозначными аналитич. ф-циями. При этомпереход с одного листа Р. п. на другой обычно интерпретируют как переходот реальных состояний частиц к виртуальным и наоборот. Др. примерами могутслужить плоскость Лобачевского и фазовые пространства динамических систем.

Лит. см. при ст. Аналитическая функция. Б. И. Завьялов.

Физическая энциклопедия. В 5-ти томах. — М.: Советская энциклопедия. Главный редактор А. М. Прохоров. 1988.