ПРОСТАЯ ПОЛУГРУППА

- полугруппа, не содержащая собственных идеалов или конгруэнции того или иного фиксированного типа. В зависимости от рассматриваемого тина возникают различные типы П. и.: идеально простая - не содержащая собственных двусторонних идеалов (термин "П. п." часто относят только к таким полугруппам), простая слева (справа) - не содержащая собственных левых (правых) идеалов, 0-простая (слева, справа) - полугруппа с нулем, не содержащая собственных ненулевых двусторонних (левых, правых) идеалов и не являющаяся двухэлементной полугруппой с нулевым умножением, бипростая - состоящая из одного -класса (см. Грина отношения эквивалентности),0-бипростая - состоящая из двух - классов, один из к-рых нулевой, простая относительно конгруэнции - не имеющая конгруэнции, кроме универсального отношения и отношения равенства.

Всякая простая слова или справа полугруппа бипроста; всякая бипростая полугруппа идеально проста, но существуют идеально П. п., не являющиеся бипростыми (и даже такие, что все их 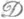-классы одноэлементны). Важнейшим типом идеально П. п. (0-простых полугрупп) является вполне простая полугруппа (вполне 0-простая полугруппа). Важнейшие примеры бипростых, но не вполне П. п.: бициклическая полугруппа, четырехспиральная полугруппа Sр ₄ (см. [11]) - это полугруппа, заданная порождающими а, b, с, d и определяющими соотношениями а ²=а, b²=b, с ²=с, d²=d, ba=a, ab=b, bc=b, cb=c, dc=c, cd=d, da=d;полугруппа Sp₄ изоморфна рисовской полугруппе матричного типа над бициклич. полугруппой с порождающими и, v, где uv=1, с сэндвич-матрицей

Четырехспиральная полугруппа является в нек-ром смысле минимальной среди бипростых и не вполне П. п., порожденных конечным числом идемпотентов, и нередко возникает как подполугруппа таких полугрупп.

Простые справа полугруппы (п. с. п.) наз. также полугруппами с правым делением или полугруппами с правой обратимостью. Основанием для этих терминов является следующее свойство таких полугрупп, эквивалентное определению: для любых элементов аи bсуществует элемент хтакой, что аx=b. П. с. п., содержащие идемпотенты,- это в точности правые группы. Важный пример п. с. п. без идешютентов доставляет полугруппа Т( М,d, р, q).всех таких преобразований j множества

М, что 1).ядро j равно отношению эквивалентности d на М,2) мощность фактормножества M/d равна р,3) множество M_j пересекается с каждым d-классом не более чем по одному элементу, 4) множество d-классов, не пересекающихся с Му, имеет бесконечную мощность q, причем . Полугруппа Т( М,d, р, q).наз. полугруппой Тесье типа ( р, q), а в случае, когда d - отношение равенства, она наз. полугруппой Бэра -Леви типа ( р, q).(см. [6], [7J). Полугруппа Тесье - пример п. с. п. без идемпотентов, не обязательно удовлетворяющей правостороннему закону сокращения. Всякая п. с. п. без идемпотентов вкладывается в подходящую полугруппу Тесье, а всякая п. с. п. без идемпотентов и с правосторонним законом сокращения вкладывается в подходящую полугруппу Бэра - Леви (причем в обоих случаях можно выбрать р=q).

Различные типы П. п. часто возникают в качестве "блоков", из к-рых строятся рассматриваемые полугруппы. По поводу классич. примеров П. п. см. Вполне простая полугруппа, Брандта полугруппа, Правая группа.;о бипростых инверсных полугруппах (в том числе структурные теоремы при нек-рых ограничениях на полурешетку идемпотентов) см. |1], [8], [9]. Существуют идеально простые инверсные полугруппы с произвольным числом -классов. При изучении вложений полугрупп в П. п. обычно либо указываются условия для возможности соответствующего вложения, либо устанавливается, что всякая полугруппа вкладывается в подходящую П. п. рассматриваемого типа; напр., любая полугруппа вкладывается в бипростую полугруппу с единицей (см. [1]), в бипростую полугруппу, порожденную идемпотентами (см. [10]), в простую относительно конгруэнции полугруппу (к-рая может обладать теми или иными наперед заданными свойствами: наличие или отсутствие нуля, полнота, пустота подполугруппы Фраттини и т. д., см. [3] - [5]).

Лит.:[1] Клиффорд А., Престон Г., Алгебраическая теория полугрупп, пер. с англ., т. 1-2, М., 1972; [2] Ляпин Е. С., Полугруппы, М., 1960; [3] Боиуть Л. А., "Сиб. матем. ж.", 1963, т. 4, N5 3, с. 500-18; [4] Шутов Э. Г., "Матем. сб.", 1963, т. 62, М5 4, с. 496-511; [5] Климов В. Н., "Сиб. матем. ж.", ! 973, т. 14, № 5, с. 1025-36; [6] Ваеr В., Lеvi F., "Sitzungsber. Heidelberg. Akad. Wiss. Math.-naturwiss. Kl.", 1932, Abh. 2, S. 3-12; [7] Теissiеr М., "Compt. rend. Acad. sci.", 1953, v. 236, № 11, p. 1120 - 22; [8] Munn W. D., в кн.: Semigroups, N. Y.- L., 1969, p. 107-23; [9] Ноwie J., An introduction to semigroup theory, L.- [a. o.], 1976; [10] Pastijn F., "Semigroup Forum", 1977, v. 14, № 3, p. 247- 263; [11] Вуleen K., Meakin J., Pastijn F., "J. Algebra", 1978, v. 54, p. 6-26. Л. Н. Шеврин.