ИНВЕРСНАЯ ПОЛУГРУППА

- полугруппа, в к-рой для любого элемента асуществует единственный инверсный к нему элемент а ^-1 (см. Регулярный элемент). Свойство полугруппы Sбыть инверсной эквивалентно каждому из следующих: S регулярная полугруппа и любые два ее идемпотента перестановочны (таким образом, множество всех идемпотентов И. п. есть полурешетка, см. Идемпотентов полугруппа);каждый левый и каждый правый главные идеалы полугруппы Sимеют единственный порождающий идемпотент. Всякая группа будет И. п., группы и только они являются И. п. с единственным идемпотентом. Важную роль при изучении И. п. играет следующее отношение остественного частичного порядка 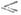на произвольной И. п. S: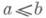тогда и только тогда, когда ab^-1=aa^-1 ( а,). На полурешетке идемпотентов И. п. оно совпадает с естественным частичным порядком этой полурешетки (см. Идемпотент). Полурешетка инверсных полугрупп (см. Связка полугрупп). будет И. п. Сдвиговая оболочка И. п. (см. Сдвиги полугрупп )также будет И. п. [7]. Всякая конгруэнция на И. п. определяется своими классами, содержащими идемпотенты.

Пусть J_X- множество всех взаимно однозначных частичных преобразований множества X(включая и "пустое преобразование" - отображение пустого множества на себя). Относительно операции суперпозиции множество J_X является И. п., к-рая наз. симметрической И. п. на множестве X. Принципиальное значение имеет следующая теорема Вагнера - Престона: произвольная И. п. Sизоморфно вложима в симметрическую И. п. J_S

Теория И. п. представляет собой один из важных и глубоко разработанных разделов теории полугрупп. Изучены представления И. п. взаимно однозначными частичными преобразованиями и матрицами над полем (см. [1]). Исследуются конгруэнции на И. п. Изучаются И. п. с условиями конечности. Выделен целый ряд важных специальных типов И. п. Накладываемые при этом ограничения по большей части либо носят характер простоты в нек-ром смысле (напр., бипростота, см. Простая полугруппа), Либо относятся к полурешетке идемпотентов Е, либо являются комбинациями условий обоих типов. Ограничения на Емогут касаться абстрактных свойств Екак полурешетки (например, Е- цепь специального вида), либо тех или иных относительных свойств Ев полугруппе, в частности поведения Еотносительно нек-рых конгруэнции. На любой И. п. Sсуществует наименьшая конгруэнция sс тем свойством, что S/sесть группа (наименьшая групповая конгруэнция), причем

И. п. наз. с-о бственной, если Есоставляет s-класс. На любой И. п. Sсуществует наибольшая конгруэнция m, разделяющая идемпотенты, причем

и mсодержится в отношении 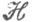(см. Грина отношения эквивалентности);И. п. наз. фундаментальной, если m совпадает с отношением равенства. Для упомянутых типов И. п. получено немало структурных теорем. При этом во многих случаях описание И. п. осуществляется "по модулю групп": группы выступают в качестве блоков различных конструкций, в к-рых участвуют также полурешетки, гомоморфизмы групп и т. п. Таковы, напр., типичные описания клиффордовых И. п. (см. Клиффордова полугруппа )и вполне О-простых И. п. (см. Брандта полугруппа).

И. п. можно рассматривать и как универсальные алгебры с двумя операциями: бинарной - умножением и унарной - взятием инверсного элемента. Получена классификация моногенных (т. е. порожденных одним элементом) И. п. как таких алгебр [6], [9]. Относительно указанных операций класс всех И. п. является многообразием; он может быть задан, напр., следующей системой тождеств [8]:

Лит.:[1] Клиффорд А., Престон Г., Алгебраическая теория полугрупп, пер. с англ., т. 1-2, М., 1972; [2] Ляпин Е. С, Полугруппы, М., 1960; [3] Курош А. Г., Общая алгебра. Лекции 1969-1970 учебного года, М., 1974; [4] Вагнер В. В., "Докл. АН СССР", 1952, т. 84, №6, с. 1119-22; [5] Preston G., "J. Lond. Math. 'Soc", 1954, v. 29, № 4, p. 396-403; [6] Глускин Л. М., "Матем. сб.", 1957, т. 41, ЛГ" 1, с. 23-36; [7] Понизовский И. С, "Успехи матем. наук", 1965, т. 20, № 6, с. 147-48; [8] Теория полугрупп и ее приложения, в. 1, Саратов, 1965, с. 286-324; [9] Ершова Т. И., "Матем. зап. Уральского ун-та", 1971, т. 8, № 1, с. 30-33; [10] Munn W. D., в кн.: Semigroups, N.Y.-L., 1969, р. 107-23; [11] О'Саrrоl . L., "J. Algebra", 1976, v. 42, р. 26-40.

Я. Я. Шеврин.