- ПОЛУИНВАРИАНТ
- общий собственный вектор семейства эндоморфизмов векторного пространства или модуля. Если G - множество линейных преобразований векторного пространства Vнад полем К, то П. множества G - это такой вектор
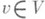 , что
, что 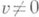 и
и 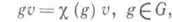 где
где  - функция, называемая весом полуинварианта v. П. веса 1 наз. также инвариантом. Чаще всего рассматривается случай, когда
- функция, называемая весом полуинварианта v. П. веса 1 наз. также инвариантом. Чаще всего рассматривается случай, когда 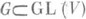 - линейная группа, тогда
- линейная группа, тогда  есть характер группы Gи продолжается до полиномиальной функции на End V. Если
есть характер группы Gи продолжается до полиномиальной функции на End V. Если  - линейное представление группы G в пространстве V, то П. группы j(G) наз. также полуинвариантом представления j. Пусть G - линейная алгебраич. группа, Н - ее замкнутая подгруппа,
- линейное представление группы G в пространстве V, то П. группы j(G) наз. также полуинвариантом представления j. Пусть G - линейная алгебраич. группа, Н - ее замкнутая подгруппа,  - алгебры Ли этих групп. Тогда существуют такое точное рациональное линейное представление
- алгебры Ли этих групп. Тогда существуют такое точное рациональное линейное представление  и такой полуинвариант
и такой полуинвариант  группы j(H), что Ни
группы j(H), что Ни 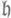 являются максимальными подмножествами в G и
являются максимальными подмножествами в G и 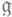 , для образов к-рых в End Евектор vесть П. Это означает, что соответствие
, для образов к-рых в End Евектор vесть П. Это означает, что соответствие 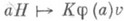 ,
,  , есть изоморфизм алгебраического однородного пространства на орбиту прямой Кv в проективном пространстве Р(Е).
, есть изоморфизм алгебраического однородного пространства на орбиту прямой Кv в проективном пространстве Р(Е).
Часто П. множества
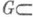 End Vназ. полиномиальную функцию на End V, являющуюся П. множеств" линейных преобразований h (G) пространства К[End V], где
End Vназ. полиномиальную функцию на End V, являющуюся П. множеств" линейных преобразований h (G) пространства К[End V], где

Если
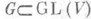 - линейная алгебраич. группа,
- линейная алгебраич. группа,  - ее алгебра Ли, то G обладает такими П.
- ее алгебра Ли, то G обладает такими П.

одинакового веса, что Gи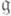 суть максимальные подмножества в GL(V) и End V, для к-рых f1, ... , fn суть П. (теорема Шевалле).
суть максимальные подмножества в GL(V) и End V, для к-рых f1, ... , fn суть П. (теорема Шевалле).
Лит.:[1] Б о р е л ь А., Линейные алгебраические группы, пер. с англ., М., 1972; [2] Хамфри Д ж., Линейные алгебраические группы, пер. с англ., М., 1980; М Шевалле К., Теория групп Ли, пер. с франц., т. 2, М., 1958.
А. Л. Онищик.
Математическая энциклопедия. — М.: Советская энциклопедия. И. М. Виноградов. 1977—1985.
