КВАДРАТИЧНЫХ ФОРМ ПРИВЕДЕНИЕ

- выделение в каждом классе квадратичных форм (к. ф.)над данным кольцом Rприведенных форм - "стандартных" форм класса (одной или нескольких). Основной целью К. ф. п. является решение проблемы эквивалентности к. ф.: установить, эквивалентны над Rданные к. ф. qи rпли нет, и в случае их эквивалентности найти (описать) все обратимые матрицы Uнад R, переводящие qв r(см. Квадратичная форма). Для решения последней задачи достаточно знать одну такую матрицу U₀ и все автоморфизмы Vформы q, ибо тогда U= VU₀. Обычно имеется в виду эквивалентность к. ф. над Z, причем часто рассматривается вся совокупность к. ф. над R и их классы над Z. Имеются принципиальные различия в теории приведения положительных (положительно определенных) и неопределенных к. ф.

Приведение положительных к. ф. Имеются различные способы приведения над Zдействительных положительных к. ф. Из них наиболее распространенный и изученный - способ приведения по Минковскому (или по Эрмнту - Минковскому), наиболее общий - по Венкову. Распространено также приведение по Зелингу (n=3) и по Шарву (n=4).

Определить приведенную к. ф.

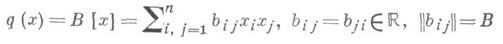
значит задать в конусе положительности B пространства коэффициентов R^N, N=n(n+1)/2, область приведения так, чтобы q(х)была приведенной тогда и только тогда, когда Желательно, чтобы обладала хорошими геометрич. свойствами (была односвязной, выпуклой и т. п.) и была фундаментальной областью группы Г целочисленных подстановок определителя Область наз. фундаментальной областью приведения положительных к. ф., если F- открытая область в R^N и: 1) для всякой к. ф. найдется эквивалентная к. ф. А q(Z), для к-рой 2) если и 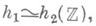то h₁ = h₂.

а) Приведение к. ф. по Минковскому. Положительная к. ф. q(x)приведена по Минковскому, если для любого k=1,... , пилюбых целых чисел l₁ ... , l_n с условием н. о. д. (l_k,..., l_n)=1,

Из бесконечного числа неравенств (1) для коэффициентов b_ij можно выбирать конечное число так, что остальные неравенства из них следуют. В пространстве коэффициентов R^N множество приведенных по Минковскому форм образует бесконечную выпуклую пирамиду (гоноэдр) с конечным числом граней, наз. областью приведения Минковского (или гоноэдром Эрмита - Минковского) -замкнутое множество, Для вычислены грани области (S_n (см. [9]).

Существует такая постоянная l_n, что если к. ф. q(x)приведена по Минковскому, то

где d(q)=det||b_ij||- определитель к. ф. q(x).

Всякая действительная положительная к. ф. эквивалентна над Zприведенной по Минковскому к. ф. Имеется алгоритм приведения (отыскания приведенной формы, эквивалентной данной) (см. [8], [15]).

Для n=2, q=q(x, у) -( а, b, с)=ах ²+2bху+су ², а, b, a>0, d(q)>0 условия приведения имеют вид

Если ограничиться собственной эквивалентностью (когда допускаются целочисленные преобразования только определителя +1), то область приведения имеет вид (условия приведения Лагранжа - Гаусса). Множество всех неэквивалентных (собственно) приведенных к. ф. записывается как объединение где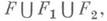

Для п=2 имеется алгоритм приведения Гаусса, согласно к-рому от формы, не удовлетворяющей условиям Лагранжа - Гаусса, следует перейти к ее "соседней":

где целое число квыбирается так, что |b'|< с/2. Для любой действительной к. ф. (a, b, с) алгоритм обрывается через конечное число шагов.

Если q=(a, b, с),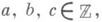н. <о. д. (а, b, с)=1, то для d(q) = ac-b²>3 имеется .лишь два автоморфизма (определителя +1), для d(q) = 3- шесть автоморфизмов, для d(g) = l -четыре автоморфизма.

б) Приведение к. ф. по Венкову. Это - способ приведения зависящий от параметра j - произвольно задаваемой действительной положительной n-арной к. ф. (см. [3]). Говорят, что к. ф. qj-приведена, если

для всех целочисленных nХn-матриц S определителя 1; здесь j=d(j)j^-1 - форма, взаимная с j, - к. ф., получающаяся из j подстановкой S,(q₁, q₂)- полуинвариант Вороного, определяемый так: если q₁=B₁[x], В ₁= q₂ = B₂[x],B₂ =то

Совокупность ф-приведенных к. ф. образует в пространстве коэффициентов R^N выпуклый гоноэдр с конечным числом граней, лежащий в Если ф=+...+x²_n и то совпадает с областью приведения

Минковского.

в) Приведение к. ф. по Зелингу и Шарву. Если в приведении по Венкову положить j=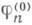=где - первая совершенная форма Вороного,то для n=3 получается приведение по Зелингу, а для n=4 - приведение по. <Шарву (см. [5], [6]).

Приведение неопределенных к. ф. принципиально сложнее, чем приведение положительных к. ф. Для них нет фундаментальных областей. Только для n=2 имеется законченная теория приведения к. ф. над Z.

а) Приведение неопределенных бинарных к. ф. Пусть q==q(x, y)=(a, b, с)=ах ²+2bху+су ²,

к. ф. определителя d=ac-b²=-|d| и |d| не есть полный квадрат. Форме qсопоставляется квадратное уравнение az²+2bz+c=0 и его различные иррациональные корни

Форма qназ. приведенной, если |W| >1, |w| <1, Ww<0. Эти условия равносильны условиям

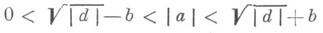
(а также условиям Число приведенных целочисленных к. ф. данного определителя конечно. Каждая к. ф. эквивалентна приведенной. Существует алгоритм приведения, использующий цепные дроби (см. [1]).

Для приведенной к. ф. существует ровно одна "соседняя справа" и ровно одна "соседняя слева" приведенная к. ф. (см. [1], с. 100). Исходя из приведенной к. ф., переходя к "соседним", получают двояко бесконечную цепь приведенных форм. Эта цепь периодична. Конечный отрезок неэквивалентных форм этой цепи наз. периодом. Две приведенные формы собственно эквивалентны тогда и только тогда, когда одна из них встречается в периоде другой.

Изложенная теория справедлива и для форм с действительными коэффициентами а, b, с, если W(q)и w(q) - различные иррациональные корни, но цепь приведенных форм при этом может не быть периодичной.

Все собственные автоморфизмы (определителя +1) к. ф. с н. о. д. ( а, b, с)=1, н. о. д. (а, 2b, с) =s, d= ас-b²<0 имеют вид

где (t, и )пробегает все решения Пелля уравнения t²+du²=s²,(T, U)- фундаментальное решение этого уравнения, т. е. наименьшее положительное решение. Несобственные автоморфизмы (определителя -1) имеются лишь у двусторонних форм - форм, класс к-рых совпадает с обратным (см. [1], с. 111). Подгруппа собственных автоморфизмов двусторонней формы имеет индекс 2 в группе всех автоморфизмов.

Неопределенные целочисленные к. ф. определителя d=-s², s>0, приводятся к виду (0, -s, r), где К. ф. (0,- s, r₁ )и (0, -s, r₂),r₂<2s

собственно эквивалентны тогда и только тогда, когда r₁ = r₂. Все автоморфизмы таких форм суть (см. [1], с. 107).

б) Приведение неопределенных n-арных к. ф. Пусть q(x) = B[х] = х ^T Вх- такая форма с действительными коэффициентами и 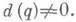Тогда существует такая подстановка переменных (над R): x=Sy, что

где (t, n-t)- сигнатура к. ф. q. Пусть

и B=S^TDS. К. ф. q(x)сопоставляется положительная к. ф.

Форма qназ. приведенной (по Эрмиту), если найдется такое преобразование Sформы qк сумме квадратов, что положительная к. ф. hs(x)является приведенной (напр., по Минковскому).

Равносильное этому определение приведенной к. ф. следующее [13], [14]. Пусть Ф (q)- множество матриц Ннад R положительных n-арных к. ф., удовлетворяющих равенству НВ ^-1 Н=В. Это связное t(n-t )-мерное многообразие конуса положительности (выписываемое в явном виде). Пусть - область приведения положительных к. ф. Форма qназ. приведенной, если не пусто.

Число классов целочисленных неопределенных к. ф. от ппеременных с данным определителем dконечно (это верно и для положительных к. ф.). Число приведенных форм в данном классе также конечно. Если две целочисленные к. ф. q₁ и q₂ эквивалентны, то найдется целочисленная подстановка S, абсолютные величины элементов к-рой ограничены постоянной, зависящей только от пи d, переводящая q₁ в q₂. Тем самым проблема установления эквивалентности или неэквивалентности двух неопределенных целочисленных к. ф. решается в конечное число шагов.

в) Автоморфизмы неопределенных к. ф. Проблема описания всех автоморфизмов неопределенной целочисленной К. ф. имеет два аспекта: 1) построить фундаментальную область группы автоморфизмов и 2) описать общий вид автоморфизмов (подобно описанию автоморфизмов через уравнение Пелля).

Общий вид автоморфизмов к. ф. был описан Ш. Эрмитом (Ch. Hermite) для n=3 и А. Кэли (А. Сауlеу) для произвольного п(см. [10]).

Построена фундаментальная область группы автоморфизмов неопределенной целочисленной к. ф. q(x)в многообразии Ф (q), ограниченная конечным числом алгебраич. поверхностей, и вычислен ее объем [13]. В случае t=1 в и-мерном пространстве переменных построена фундаментальная область группы автоморфизмов к. ф. q(x)в виде бесконечной пирамиды с конечным числом плоских граней [2], [4].

Построена теория приведения к. ф. в алгебраич. числовых полях (см. [11]).

Лит.:[1] Венков Б. А., Элементарная теория чисел, М.-Л., 1937; [2] его же, "Изв. АН СССР. Сер. матем.", 1937, т. 1, с. 139-70; [3] его же, там же, 1940, т. 4, с. 37-52; [4] его же, "Тр. Матем. ин-та АН СССР", 1951, т. 38, с. 30- 41; [5] Делоне Б. Н., "Успехи матем. наук", 1937, в. 3, с. 16-62; 1938, в. 4, с. 104-64; [6] Делоне Б. Н., Галиулин Р. В., Шторгин М. П., в кн.: Современные проблемы математики, т. 2, М., 1973, с. 119-254; [7] Делен-Дирихле П. Г., Лекции по теории чисел, пер. с нем., М.- Л.. 1936; [8] Рынков С. С, "Зап. науч. семинаров ЛОМИ", 1973, т. 33, с. 37-64; [9] Таммела П. П., там же, 1975, т. 50, с. 6-96; 1977, т. 67, с. 108-43; [10] Bachmann P., Die Arithmetik der quadratischen Formen, Abt. 1-2, Lpz., 1923-25; [11] Humbert P., "Comment, math, helv.", 1949, t. 23, p. 50- 63; [12J Minkowski H. "J. reine und angew. Math.", 1905, Bd 129, S. 220-74; [13]Siegel С L., "Abh. Math. Semin. Univ. Hamburg", 1940, Bdl3, S. 209-39; [14] eго же, "Nachr. Akad. Wiss. Gottineen. Math.-phys. Kl.", 1972, S. 21-46; [15] Van der Waerden B. L., "Acta math.", 1956, v. 96, p. 265-309.

А. В. Малышев.