Кумулянты

Общие сведения

Полуинварианты или кумулянты были введены датским астрономом и математиком Торвальдом Николаем Тиле в 1889 году (по другим данным в 1903 году). Заметим что в русском языке иногда также используется название семиинварианты (от латинского semi- т.е полу-, половина), но оно в принципе не может считаться правильным, т.к. в русском языке всё-таки не говорят семипроводник, ни семикондуктор, а говорят полупроводник. Тиле называл эти статистические величины полуинвариантами (semi-invariant) и до 30-ых годов XX-ого столетия их так и называли, но в 30-ых годах английский статистик Фишер предпочёл использовать название кумулянты (анг. cumulants), ввиду их кумулятивных, т.е. накопительных свойств, и со временем именно это название и закрепилось в литературе. Тем не менее, в русскоязычной литературе, предпочтение всегда отдавалось оригинальному названию, например Ширяев использует только лишь оригинальное латинское название. Кстати, для обозначения полуинвариант почти всегда используется греческая буква κ, хотя Ширяев использует ξ.

Несмотря на то что введены полуинварианты были давно, до 30-ых годов XX-ого века им уделяли очень мало внимания; только лишь в конце 30-ых годов английский учёный, сэр Рональд Эйльмер Фишер (анг. Sir Ronald Aylmer Fisher) впервые провёл систематическое исследование полуинвариант. На сегодняшний день, полуинварианты прочно вошли в мир современной статистики и её приложений; в частности, они очень широко используются в области обработки сигналов. Последнее легко понять, т.к. например все полуинварианты третьего и более высоких порядков равны нулю для нормальных процессов, смешанные полуинварианты всех порядков статистически независимых величин равны нулю, и пр. Кстати, последнее свойство практически теперь ложится в основу определения статистической независимости: вместо стандартного определения независимости через функцию распределения часто говорят о статистической независимости двух величин до n-ого порядка, подразумевая под этим не вышеупомянутое определение, а то, что все смешанные полуинварианты порядка до n (включительно) равны нулю.

Определение через характеристическую функцию

Полуинварианты, в отличие от моментов, не могут быть определены напрямую через функцию распределения p(x). Их определяют либо через логарифм характеристической функции G(u), либо через моменты μ (второе определение на самом деле вытекает из первого). Формально, полуинварианты определяются как коэффициэнты в разложении в ряд МакЛорена логарифма характеристической функции, образом, в точности аналогичному тому, которым есть моменты для самой характеристической функции, т.е. с вынесенными вперёд коэффициэнтами iⁿ:

$\ln G(u) \, = \, iu\kappa_1 + \frac{(iu)^2}{2!}\kappa_2 + \ldots +\frac{(iu)^n}{n!} \kappa_n + \ldots = \sum\limits_{n=1}^{\infty}\frac{(iu)^n}{n!} \kappa_n$

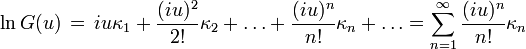
Единственная разница состоит в том что первый член этого ряда полагается равным 0, а не 1 как это есть для моментов. Кстати, сам логарифм характеристической функции, ввиду важности полуинвариант генерирующей функцией которых он является, также получил отдельное название, его иногда называют второй характеристической функцей, и даже через что-нибудь такое обазначают, например:

$\varphi(u)\,\equiv\,\ln G(u)$

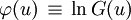
Тогда, очевидно что из определения ряда МакЛорена, полуинварианта порядка n будет определена как:

$\kappa_n \,=\, (-i)^n \left.\frac{\,\partial^n\varphi}{\,\partial u^n}\right|_{u=0}$

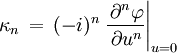
и для первой полуинварианты всё намного проще:

$\kappa_1 \,=\, -i \left.\frac{\,\partial\varphi}{\,\partial u}\right|_{u=0}\,=\,-i \left.\frac{G'_u}{\,G(u)}\right|_{u=0}$

Две последние формулы и есть определение полуинвариант через характеристическую функцию.

Определение через моменты

Выведем теперь альтернативное определение полуинвариант через моменты. Разлагая характеристическую функцию G(u) в ряд МакЛорена через моменты, мы можем переписать первую формулу в следующем виде:

$\ln \left\{1+\sum\limits_{n=1}^{\infty}\frac{(iu)^n}{n!} \mu_n \right\} \, = \,\sum\limits_{n=1}^{\infty}\frac{(iu)^n}{n!} \kappa_n$

Теперь, разлагая и логарифм в ряд МакЛорена, и предполагая что условия на его радиус сходимости выполняются, мы получим:

$\sum\limits_{m=1}^{\infty}(-1)^{m+1}\frac{\displaystyle\left(\sum\limits_{n=1}^{\infty}\frac{(iu)^n}{n!} \mu_n \right)^{\!\!m} }{m} \,=\,\sum\limits_{n=1}^{\infty}\frac{(iu)^n}{n!} \kappa_n$

Далее надо аккуратно расписать все члены стоящие в суммах слева и справа и попросту приравнять коэффициенты при равных степенях iu. Тогда мы легко получим следующие выражения:

$\begin{cases} \kappa_1=\mu_1 \\[1mm] \kappa_2=-\mu^2_1+\mu_2 \\[1mm] \kappa_3=2\mu^3_1-3\mu_1\mu_2 +\mu_3 \\[1mm] \;\ldots\ldots\ldots\ldots\ldots\ldots\ldots \end{cases}$

Ну правда „легко“ на этом и кончается, и затем всё очень сильно усложняется. Интересный метод основанный на производной для более простого отыскания этих взаимоотношений, а также эти выражения для более высоких порядков описаны у Кендалла. Он также даёт общую формулу для отысканий моментов через полуинварианты и обратно, эта же формула встречается и у Ширяева. Кстати, эту общую формулу в некоторой литературе так и называют формулой Ширяева-Леонтьева, хотя по всей видимости они не были первыми кто её вывели.