ПЕРРОНА МЕТОД

ПЕРРОНА МЕТОД

- метод решения Дирихле задачи для Лапласа уравнения, основанный на свойствах субгармонических функций (и супергармонич. функций). Первоначальное изложение этого метода было дано О. Перроном [1], существенное развитие получено в работах Н. Винера [3] и М. В. Келдыша [4].

Пусть W - коночная область евклидова пространства с границей - действительная функция на . Пусть Ф - (непустое) семейство всех супергармонич. функций

в широком смысле (т. е. функция принадлежит Ф), ограниченных снизу и таких, что


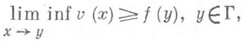
и пусть


- нижняя огибающая семейства Ф. Наряду с Ф рассматривается (непустое) семейство Y всех субгармонич. функций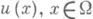 , в широком смысле (функция u(x) ), ограниченных сверху и таких, что


и пусть


- верхняя огибающая семейства Y. Относительно функци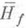и (и ) имеются только

три возможности: - гармонич. функция, причем всегда


Функция 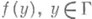, наз. разрешимой, если обе огибающие 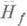и 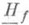конечны и совпадают. В этом случае гармонич. функция 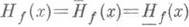есть обобщенное решение задачи Дирихле для функции (в смысле Винера - Перрона).

Для того чтобы функция , была разрешимой, необходимо и достаточно, чтобы она была интегрируемой по гармонич. мере на Г (теорема Брело). Любая непрерывная конечная функция , разрешима (теорема Винера).

Точка наз. регулярной граничной точкой, если для любой непрерывной конечной функции 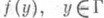, выполняется предельное соотношение


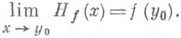
Регулярность всех точек равносильна существованию классич. решения wf(x).задачи Дирихле для любой непрерывной конечной функции 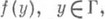причем в этом случае ; область W, все граничные точки к-рой регулярны, иногда наз. также регулярной. Для того чтобы точка была регулярной, необходимо и достаточно, чтобы существовал барьер в у 0.

Точки , не являющиеся регулярными, наз. иррегулярными граничными точками. Напр., иррегулярными граничными точками являются изолированные точки и при вершины достаточно сильно заостренных входящих в область W острий (пример Лебега). Множество всех иррегулярных точек Г есть множество типа Fs емкости нуль.

Пусть имеется последовательность областей Wk, , такая, что , и непрерывная конечная функция , продолжена непрерывно на окрестность Г. Тогда


равномерно внутри W; в случае регулярных областей Wk здесь получается конструкция обобщенного решения задачи Дирихле по Винеру. Рассмотрим теперь для области W без внутренней границы произвольную последовательность областей В этом случае, вообще говоря,


Задача Дирихле устойчива в области W или в замкнутой области 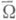, если


соответственно для всех 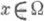или для всех . Для устойчивости задачи Дирихле в области W. необходимо и достаточно, чтобы множества всех иррегулярных точек дополнений CW. и 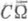совпадали; для устойчивости в замкнутой области - чтобы дополнение не имело иррегулярных точек (теоремы Келдыша, см. [4], где построен также пример регулярной области W, внутри к-рой задача Дирихле неустойчива). См. также Верхних и нижних функций метод. Лит.:[1] Perron О., "Math. Z.", 1923, Bd 18, S. 42-54; [2] Петровокий И. Г., "Успехи ыатем. наук",. 1941 [1940], в. 8, с. 107-14; [3] Wiеnеr N., "J. Math, and Phys.", 1924, v. 3, p. 24-51, 127-46; 1925, v. 4, p. 21-32; [41 Келдыш М. В., "Успехи матем. наук", 1941 [1940], п. 8, с. 171 - 231; [5] Брело М., Основы классической теории потенциала, пер. с франц., М., 1964. Е. Д. Соломенцев.


Математическая энциклопедия. — М.: Советская энциклопедия. . 1977—1985.

Игры ⚽ Нужен реферат?

Полезное


Смотреть что такое "ПЕРРОНА МЕТОД" в других словарях:

  • ВЕРХНИХ И НИЖНИХ ФУНКЦИЙ МЕТОД — метод доказательства существования решения краевых задач для дифференциальных уравнений. Идея В. н н. ф. м. для случая обыкновенных дифференциальных уравнений усматривается в работах Дж. Пеано (G. Peano, 1880), для случая Дирихле задачи и для… …   Математическая энциклопедия

  • ПОТЕНЦИАЛА ТЕОРИЯ — в первоначальном понимании учение о свойствах сил, действующих по закону всемирного тяготения. В формулировке этого закона, данной И. Ньютоном (I. Newton, 1687), речь идет только о силах взаимного притяжения, действующих на две материальные… …   Математическая энциклопедия

  • ДИРИХЛЕ ЗАДАЧА — задача отыскания регулярной в области Dгармонич. функции u, к рая на границе Г области Dсовпадает с наперед заданной непрерывной функцией j. Задачу отыскания регулярного в области решения эллиптич. уравнения 2 го порядка, принимающего наперед… …   Математическая энциклопедия

  • КЕЛДЫША ТЕОРЕМА — 1) К. т. о приближении непрерывных функций многочленами: пусть функция f(z) комплексного переменного z голоморфна в области Gи непрерывна в замкнутой области тогда, для того чтобы при любом e>0 существовал многочлен P(z)такой, что необходимо и …   Математическая энциклопедия

  • ГАРМОНИЧЕСКОЕ ПРОСТРАНСТВО — топология, пространство X с пучком непрерывных действительных функций с аксиоматически фиксируемыми в той или иной форме тремя основными свойствами классических гармонических функций:свойство сходимости, выражаемое второй Гарнака теоремой;принцип …   Математическая энциклопедия

  • ИРРЕГУЛЯРНАЯ ГРАНИЧНАЯ ТОЧКА — точка у 0 границы Г области D, для к рой существует такая непрерывная граничная функция f(y)на Г, что обобщенное решение Дирихле задачи в смысле Винера Перрона (см. Перрона метод) и (х)не принимает в точке у 0 граничного значения f(y0), т. е.… …   Математическая энциклопедия

  • КЕЛЛОГА - ЭВАНСА ТЕОРЕМА, — лемма Келлога: множество всех иррегулярных точек границы произвольной области Dевклидова пространства Rn, относительно обобщенного решения Дирихле задачи для Dв смысле Винера Перрона (см. Перрона метод )имеет нулевую емкость, является полярным… …   Математическая энциклопедия

  • РЕГУЛЯРНАЯ ГРАНИЧНАЯ ТОЧКА — точка y0 границы Г области Dевклидова пространства , в к рой для любой непрерывной на Г функции f(y)обобщенное решение u (x) Дирихле задачи в смыслеВинера Перрона (см. Перрона метод).принимает граничное значение , то есть Р. г. т. для области… …   Математическая энциклопедия

  • РИМАНОВЫХ ПОВЕРХНОСТЕЙ КЛАССИФИКАЦИЯ — изучение римановых поверхностей (р. п.), связанное с рассмотрением поведения функций различных классов на этих поверхностях. Комплексная функция на р. п. Rназ. а н а л и т и ч е с к о й на R, если для любой точки существуют окрестность Uи… …   Математическая энциклопедия

  • КРАЕВАЯ ЗАДАЧА — для уравнения с частными производными задача определения в нек рой области Dпеременных решения u(x) уравнения удовлетворяющего на границе Sэтой области (или ее части) определенным краевым условиям Как правило, краевые условия связывают граничные… …   Математическая энциклопедия


Поделиться ссылкой на выделенное

Прямая ссылка:
… Нажмите правой клавишей мыши и выберите «Копировать ссылку»