КЕЛДЫША ТЕОРЕМА

- 1) К. т. о приближении непрерывных функций многочленами: пусть функция f(z) комплексного переменного z голоморфна в области Gи непрерывна в замкнутой области 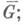тогда, для того чтобы при любом e>0 существовал многочлен P(z)такой, что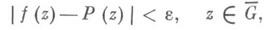

необходимо и достаточно, чтобы дополнение 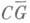состояло из одной единственной области G*, содержащей бесконечно удаленную точку. Установлена М. В. Келдышем [1]. Эта теорема является одним из основных результатов теории равномерных приближений функций многочленами в комплексной области (см. [2]). 2) К. т. в теории потенциала - теоремы о разрешимости и устойчивости Дирихле задачи, установленные М. В. Келдышем в 1938-41.

а) Пусть D- ограниченная область евклидова пространства Rⁿ,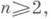. с границей Y=дD. Тогда на Г существует счетное множество иррегулярных граничных точек {y_k}, k=1, 2, ..., такое, что для разрешимости задачи Дирихле в области Dс непрерывной граничной функцией f(y)на Г необходимо и достаточно, чтобы эта задача была разрешима в точках у _k, k=1,2, ..., т. е. чтобы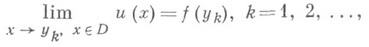

где и(х)- обобщенное в смысле Винера - Перрона решение задачи Дирихле (см. Перрона метод, а также [3], [4]).

б) Пусть оператор Адействует из пространства С(Г) непрерывных функций на Г в пространство ограниченных гармонических в Dфункций и удовлетворяет следующим условиям: (а) А(af+bg) = aA (f)+bA(g),

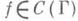где a, b - действительные числа, т. е. оператор Алинейный; (б) если то А(f)(х)0; (в) если для функции задача Дирихле разрешима, то А(f) дает решение этой задачи. При этих условиях оператор Аединственный и А(f) для всех 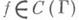дает обобщенное в смысле Винера - Перрона решение задачи Дирихле (см. [5]-[7]).

в) Для того чтобы всякая разрешимая в Dзадача Дирихле была устойчивой в 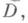необходимо и достаточно, чтобы множество иррегулярных граничных точек множества совпадало с множеством иррегулярных граничных точек множества CD. Задача Дирихле с любой функцией устойчива внутри Dтогда и только тогда, когда множество иррегулярных граничных точек 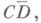принадлежащих Г, имеет в Dгармонич. меру нуль (см. [4]).

Лит.:[1] Келдыш М. В., "Матем. сб.", 1945, т. 16, № 3, с. 249-58; [2] Мергелян С. Н., "Успехи матем. наук", 1952, т. 7, в. 2, с. 3-122; [3] Келдыш М. В., "Докл. АН СССР", 1938, т. 18, с. 315-18; [4] его же, "Успехи матем. наук", 1941, т. 8, с. 171-292; [5] его же, "Докл. АН СССР", 1941, т. 32, с. 308-9; [6] Ландкоф Н. С, Основы современной теории потенциала, М., 1966, гл. 4, 5; [7] Брело М., Основы классической теории потенциала, пер. с франц., М., 1904.

Е. Д. Соломепцев.