НЕЛИНЕЙНЫЙ ОПЕРАТОР

- отображение А векторного (как правило) пространства Xв векторное пространство Yнад общим полем скаляров, не обладающее свойством линейности, т. е. такое, что, вообще говоря,

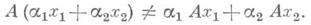
Если 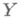есть множество действительных чисел 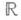или комплексных чисел , то Н. о. наз. нелинейным функционалом. Простейшим примером Н. о. (нелинейного функционала) служит действительная функция действительного аргумента, отличная от линейной функции.

Одним из важных источников возникновения Н. о. являются задачи математич. физики. Если при составлении локального математич. описания процесса учитываются малые не только первого, но и высших порядков, то возникают уравнения с Н. о. К нелинейным операторным уравнениям приводят также нек-рые задачи математич. экономики, авторегулирования, теории управления и т. д.

Примеры нелинейных операторов.

где 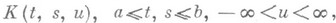- такая функция, что 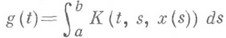есть непрерывная на [ а, b]. функция для любой функции (напр., K(t, s, и )непрерывна на 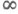). Если нелинейна по и, то А- нелинейный оператор Урысона, отображающий С[ а, b]в С[ а, b]. При других ограничениях на 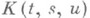оператор Урысона действует в других пространствах, напр, в L₂[a, b], или отображает одно пространство Орлича .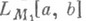в другое .

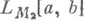где 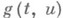- нелинейная по ифункция, определенная на . При соответствующих ограничениях на оператор Вдействует из одного функционального пространства в другое и наз. нелинейным оператором Гаммерштейна.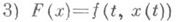

- оператор суперпозиции, наз. также оператором Немыцкого, преобразующий при соответствующих ограничениях на нелинейную по 2-му аргументу функцию пространство измеримых функций x(t)в себя.

- нелинейный дифференциальный оператор порядка 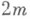дивергентного вида, действующий в пространстве Соболева при соответствующих ограничениях на нелинейные функции 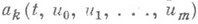. Здесь к- мультииндекс и G- ограниченная область пространства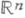

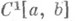- нелинейный интегро-дифференциальный оператор, действующий при соответствующих ограничениях на функцию в пространстве непрерывно дифференцируемых функций.

На Н. о., действующие из одного топологического векторного пространства Xв другое топологическое векторное пространство Y, переносятся многие понятия и операции математич. анализа действительных функций действительного переменного. Так, Н. о. наз. ограниченным, если - ограниченное множество в Y для любого ограниченного множества ; Н. о. Анепрерывен в точке 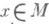, если прообраз окрестности точки Ах содержит для нек-рой окрестности точки х. Как и для функции, Н. о., непрерывный в каждой точке компактного множества М, ограничен на этом множестве. В отличие от линейных операторов, для Н. о., действующих в нормированных пространствах, из ограниченности оператора Ана нек-ром шаре не следует непрерывность Ана этом шаре.

Однако в нек-рых случаях из непрерывности (ограниченности) Н. о. на шаре следует непрерывность (ограниченность) оператора во всей области его определения. Среди Н. о., действующих пз Xв Y, можно выделить нек-рые важные классы.

1)Полилинейные операторы А:

: линейные по каждому аргументу.

Пространство (I) всех n-линейных операторов изоморфно пространству 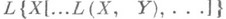(II), где - пространство всех линейных операторов из Xв Y. Если Xи Y - нормированные пространства, то пространства (I) и (II) изометричны. Если Асимметричен по всем аргументам, то обозначается и наз. однородным оператором n-й степени.

2) В пространствах, наделенных частичной упорядоченностью,- изотонные операторы Аи антитонные операторы , характеризующиеся соответственно условиям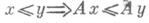и и 3) В гильбертовом пространстве H - монотонные операторы М, определяемые условием для любых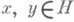

4) Компактные операторы, преобразующие ограниченные подмножества своей области определения в предкомпактные множества, в том числе вполне непрерывные операторы, являющиеся одновременно компактными и непрерывными.

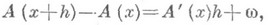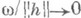Для Н. о. нетривиальными и полезными являются понятия дифференциала и производной. Оператор А, действующий из открытого множества Gнормированного векторного пространства X в нормированное векторное пространство Y, наз. дифференцируемым по Фреше в точке , если существует линейный непрерывный оператор такой, что для любого , для к-рого имеет место где при 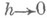. В этом случае линейная по hчасть 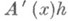приращения наз. дифференциалом Фреше оператора Ав точке хи обозначается , а 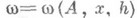наз. остатком приращения. Линейный ограниченный оператор А' (х)наз. производной Фреше оператора Ав точке х. Помимо дифференцируемости по Фреше вводится дифференцируемость по Гатв. Именно, оператор Аназ. дифференцируемым по Гато в точке х, если существует

наз. дифференциалом Гато оператора А в точке х. Дифференциал Гато однороден по h, т. е. . Если DA(x, h )линеен по hи 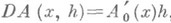, то линейный оператор наз. производной Гато оператора А. Из дифференцируемости по Фреше следует дифференцируемость по Гато и равенство 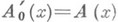. Из дифференцируемости по Гато не следует в общем случае дифференцируемость по Фреше, но если 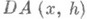существует в окрестности точки х, непрерывен по hи равномерно непрерывен по х, то Адифференцируем по Фреше в точке х. Для нелинейных функционалов дифференциалы и производные Фреше и Гато определяются аналогично. При этом производная Гато наз. градиентом функционала fи является оператором из 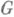в 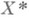. Если 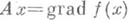для нек-рого нелинейного функционала f, то оператор Аназ. потенциальным.

Для операторов, действующих в отделимых топологических векторных пространствах, возможно несколько определений дифференцируемости. Пусть - нек-рая совокупность ограниченных множеств топологического векторного пространства X. Отображение наз.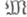 -м алым, если для любого 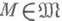имеет место при равномерно но . Отображение ( 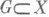и открыто) наз. 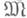-дифференцируемым в точке , если

где 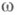есть 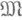-малое отображение. Чаще всего в качестве берется либо совокупность всех ограниченных множеств, либо совокупность всех компактных множеств, либо совокупность всех конечных множеств пространства X. Для Н. о. в нормированных пространствах первый случай приводит к дифференцируемости по Фреше, третий - к дифференцируемости по Гато. Обычным образом, как производные от производных, определяются производные высших порядков и оператора А. Это - полилинейные симметрич. отображения. Дифференциалом n-го порядка будет при этом однородная форма n-й степени . Возможны иные определения высших производных. Пусть, напр., Xи Y - нормированные векторные пространства,- открыто, . Если для любого hтакого, что ,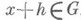

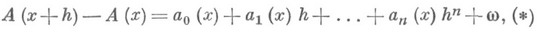
где , то полилинейная форма наз. производной k-го порядка. Выражение (*) наз. при этом ограниченным разложением n-го порядка разности При выполнении соответствующих ограничений различные определения высших производных эквивалентны.

Если в пространстве Xзадана скалярная счетно аддитивная мера, то Н. о. можно интегрировать, понимая в смысле Бохнера интеграла. Для Н. о. , как и в случае линейного, значения параметра 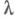такие, что 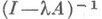существует и непрерывен на (М), естественно назвать регулярными, а остальные точки 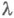отнести к спектру. По своим свойствам спектр Н. о. Аможет резко отличаться от спектров линейных операторов. Так, спектр вполне непрерывного Н. о. может иметь непрерывные участки; из собственного элемента х ₀ оператора А, т. е. такого, что могут выходить ветви собственных элементов, и т. п.

Лит.:[1] Люстерник Л. А., Соболев В. И., Элементы функционального анализа, 2 изд., М., 1965; [2] Канторович Л. В., Акилов Г. П., Функциональный анализ, 2 изд., М., 1977; [3] Вайнберг М. М., Вариационные методы исследования нелинейных операторов, М., 1956; [4] Красносельский Ж. А., Забрейко П. П., Геометрические методы нелинейного анализа, М., 1975; [5] Гаевский X., Грёгер К., Захариас К., Нелинейные операторные уравнения и операторные дифференциальные уравнения, пер. с нем., М., 1978.

В. И. Соболев.