- НЕЯВНЫЙ ОПЕРАТОР
- решение y=f(x). нелинейного операторного уравнения F(x, y)=0, в к-ром хиграет роль параметра, а у- неизвестного. Пусть X, Y, Z- банаховы пространства, F(x, у)- нелинейный оператор, непрерывный в окрестности
точки 
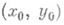
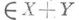и отображающий 
в окрестность нуля в Z. Если Фреше производная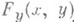
. непрерывна в 
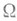, существует и ограничен оператор 
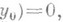то найдутся числа 
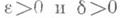такие, что при 
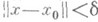в шаре 
уравнение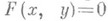 
имеет единственное решение 
. При этом Н. о.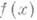 
непрерывен по 
и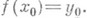 
Если дополнительно 
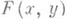праз дифференцируем в 
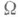, то и 
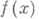п раз дифференцируем. Если 
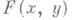- аналитический оператор в 
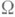, то и f(х)- аналитический. Эти утверждения обобщают известные предложения о неявных функциях. О вырожденных случаях см. Ветвление решений нелинейных уравнений.Лит.:[1] Hildebrandt Т. Н., Graves L. М., "Trans. Amer. Math. Soc", 1927, v. 29, p.127 -53; [2] Люcтерник Л. А., Соболев В. И., Элементы функционального анализа, 2 изд., М., 1965; [3] Вайнберг М. М., Треногий В. А., Теория ветвления решений нелинейных уравнений, М., 1969; [4] Ниренберг Л., Лекции по нелинейному функциональному анализу, пер. с англ., М., 1977.
В. А. Треногий.
Математическая энциклопедия. — М.: Советская энциклопедия. И. М. Виноградов. 1977—1985.
