ЛОКАЛЬНАЯ СТРУКТУРА ТРАЕКТОРИЙ

квадратичного дифференциала - описание поведения траекторий квадратичного дифференциала на ориентированной римановой поверхности в окрестности любой точки этой поверхности. 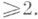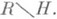Пусть R - ориентированная риманова поверхность, Q(z)dz² - квадратичный дифференциал на R; пусть С - множество всех нулей и простых полюсов Q(z)dz²,a H - множество всех полюсов Q(z)dz² порядка Траектории Q(z)dz² образуют регулярное семейство кривых на При нек-ром расширении понятия регулярного семейства кривых это остается верным и на Поведение траекторий в окрестностях точек множества Нявляется значительно более сложным. Полное описание Л. с. т. приводится ниже.

1) Для любой точки существуют окрестность Nточки Р на Л и гомеоморфное отображение Nна круг такие, что максимальная открытая дуга каждой траектории из Nпереходит в отрезок, на к-ром vпостоянно. Следовательно, через каждую точку из проходит траектория дифференциала Q(z)dz², являющаяся либо открытой дугой, либо жордановой кривой на R.

2) Для любой точки 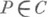_ порядка m (m>0, если Р- нуль, и m=-1, если Р - простой полюс) существуют окрестность Nточки Рна Rи гомеоморфное отображение Nна круг |w|<1 такие, что максимальная дуга каждой траектории из Nпереходит в открытую дугу, на к-рой 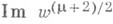постоянна. Существуют m+2 траекторий с концами в Р и с предельными касательными направлениями, составляющими друг с другом равные углы величины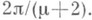

3) Пусть __ - полюс порядка m>2. Если нек-рая траектория имеет конец в Р, то она стремится к Рпо одному из m-2 направлений, расположенных под равными углами 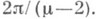Существует окрестность Nточки Рна Rсо следующими свойствами: (1) каждая траектория, проходящая через нек-рую точку окрестности N, в каждом из направлений либо стремится к Р, либо выходит из N;(2) существует окрестность N* точки Р, содержащаяся в Nи такая, что каждая траектория, проходящая через нек-рую точку из N*, хотя бы в одном направлении стремится к Р, оставаясь в N*; (3) если нек-рая траектория целиком лежит в Nи поэтому в обоих направлениях стремится к Р, то касательная к этой траектории при приближении к Рв соответствующем направлении стремится к одному из двух смежных предельных положений. Жорданова кривая, полученная присоединением к этой траектории точки Р, ограничивает область D, содержащую точки угла, образованного двумя соседними предельными касательными. Касательная к любой траектории, имеющей общие точки с D, стремится при приближении к Рв двух направлениях соответственно к этим смежным предельным положениям. Область Dотображается с помощью надлежащей ветви функции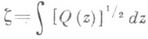

на полуплоскость ( с - действительное число); (4) для каждой пары смежных предельных положений существует траектория, обладающая свойствами, описанными в (3).

4) Пусть 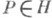- полюс 2-го порядка и z - локальный параметр, в терминах к-рого Р представляется точкой z=0. Пусть 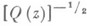имеет (при нек-ром выборе ветви корня) следующее разложение в окрестности точки z=0:

где а, b - действительные, b₁ ,b₂, . . . - комплексные постоянные. Строение образов траекторий дифференциала Q(z)dz² в плоскости z определяется тем, какой из следующих трех случаев имеет место.

Случай I: 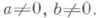Для достаточно малого a>0 образ каждой траектории, пересекающей круг |z|<a, в одном направлении стремится к z=0, а в другом - выходит из круга |z|<a. И модуль, и аргумент z изменяются монотонно на образе траектории в круге |z|<a. Каждый образ траектории закручивается около точки z=0 и ведет себя асимптотически, как логариф-мич. спираль.

Случай II: Для достаточно малого a>0 образ каждой траектории, пересекающей круг |z|<a, в одном направлении стремится к z=0, а в другом - выходит из круга |z|<a. Модуль z изменяется монотонно иа образе траектории в круге |z|<a. Разные образы траекторий имеют разные предельные направления в точке z=0.

Случай III: Для каждого e>0 можно найти такое число a(e)>0, что при 0<a<a(e) образ траектории, пересекающей окружность |zl=a, представляет собой жорданову кривую, лежащую в круговом кольце

Лит.:[1] Дженкинс Дж., Однолистные функции и конформные отображения, пер. с англ., М., 1962.

Г. В. Кузьмина.